Дифференциальная пара на MOSFET транзисторах с активной нагрузкой: измерение лямбды, прогнозирование усиления

В данной статье мы рассмотрим формулу для дифференциального усиления и используем LTspice, чтобы найти значение параметра модуляции длины канала, называемого лямбда (λ).

Вспомогательная информация

• Схемы на дискретных полупроводниковых компонентах: Дифференциальный усилитель
• Схемы на дискретных полупроводниковых компонентах: Простой операционный усилитель на дискретных элементах
• Полевые транзисторы с изолированным затвором (MOSFET)
• Базовая схема источника стабилизированного тока на MOSFET транзисторах
• Базовая схема дифференциальной пары на MOSFET транзисторах

Предыдущие статьи

• Дифференциальная пара на MOSFET транзисторах с активной нагрузкой
• Преимущества дифференциальной пары на MOSFET транзисторах с активной нагрузкой
• Дифференциальная пара на MOSFET транзисторах с активной нагрузкой: выходное сопротивление

Дифференциальная пара с выходным сопротивлением

В предыдущей статье мы обсуждали выходное сопротивление MOSFET транзистора для малых сигналов (r_вых): почему оно существует, как оно влияет на схему усилителя и как его рассчитать. Теперь мы будем использовать этот новый опыт для изучения усиления дифференциальной пары с активной нагрузкой. Начнем со следующей схемы:

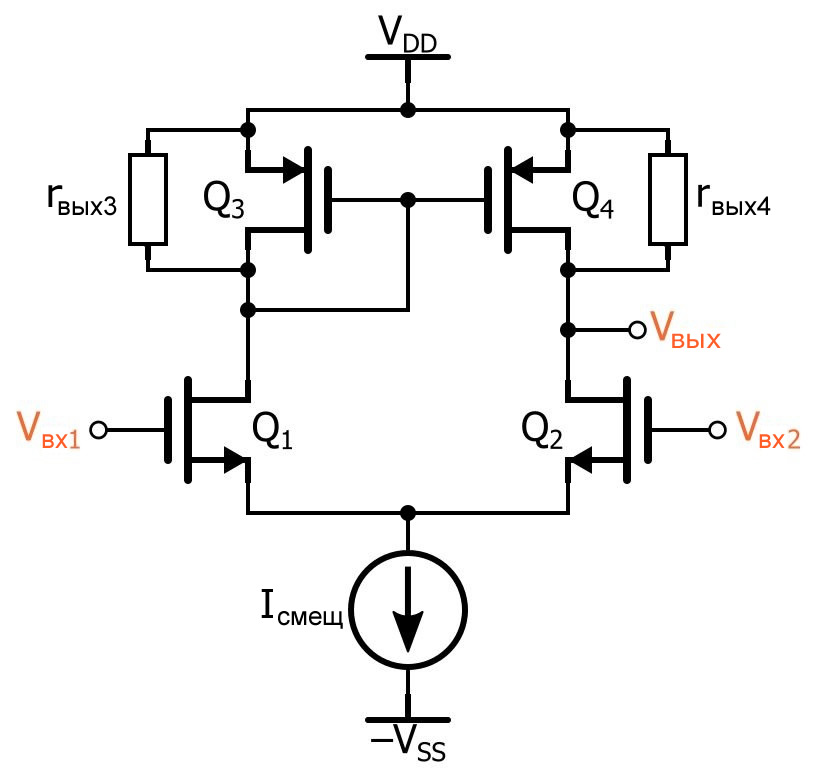
Итак, теперь у нас есть сопротивления в цепях стока полевых транзисторов усилителя, что делает схему с активной нагрузкой похожей на версию с резисторами стока, представленную в статье «Базовая схема дифференциальной пары на MOSFET транзисторах». Полный анализ дифференциального усиления для этой схемы не так прост, и я не хочу зацикливаться на сложности всего этого. Вместо этого мы применим абстрактный, интуитивный подход.

Самый простой способ – предположить, что схема симметрична, а затем проанализировать только правую часть дифференциальной пары (потому что выходной сигнал берется с правой стороны). Этот метод был бы хорош для дифференциальной пары с резисторами стока, потому что та схема фактически симметрична, если мы предполагаем идеальное согласование параметров. Но дифференциальная пара с активной нагрузкой, к сожалению, не симметрична.

Однако оказывается, что мы можем притвориться, что схема симметрична, а затем выполнить интуитивный анализ с правой стороной пары. При этом мы можем получить правильное выражение для дифференциального усиления.

Может быть, вам не нравится такое безрассудное пренебрежение к строгой теории цепей, но я просто рад, что могу изучить и (хотя бы частично) понять ситуацию, не теряясь в деталях.

«Интуитивный» анализ

Итак, давайте разделим схему пополам и предположим, что к истоку Q₂ подключена виртуальная земля.

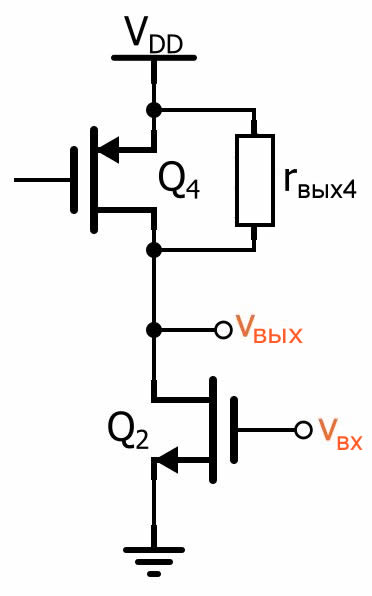
Мы видим, что схема напоминает правую часть дифференциальной пары в версии с резистором стока. Как указывалось в статье «Базовая схема дифференциальной пары на MOSFET транзисторах», величина дифференциального усиления полной дифференциальной пары с резисторами стока равна (g_m × R_с), и это означает, что коэффициент усиления одной половины дифференциальной пары с резисторами стока (A_V,оп) равен этому же выражению, деленному на два:

\[A_{V,оп}=\frac{g_m\times R_с}{2}\]

Мы можем применить это же выражение к паре с активной нагрузкой, где резистором стока теперь является выходное сопротивление Q₄ для малых сигналов. Однако не забывайте, что дифференциальная пара преобразует выходной сигнал из дифференциального в несимметричный без потери усиления – другими словами, уменьшение коэффициента усиления в два раза, которое происходит, когда мы разделяем дифференциальную пару с резисторами стока, не применяется к схеме с активной нагрузкой.

Таким образом, можно сделать вывод, что коэффициент усиления дифференциальной пары с активной нагрузкой (A_V,ан) будет равен:

\[A_{V,ан}=g_m\times r_{вых4}\]

Но это было бы неправильно! Это неправильно, потому что мы забываем о выходном сопротивлении Q₂. При использовании дифференциальной пары с резисторами стока игнорировать выходное сопротивление Q₂ более оправданно, поскольку оно, вероятно, намного больше, чем резистор стока. Как мы видели в усилителе с общим истоком, рассмотренном в предыдущей статье, анализ для малых сигналов помещает выходное сопротивление параллельно резистору стока.

Если r_вых намного больше, чем R_с, параллельная схема не будет сильно отличаться от R_с. Но со схемой с активной нагрузкой у нас совершенно новая ситуация: r_вых от Q₄, вероятно, будет очень похоже на r_вых от Q₂, и, таким образом, мы не можем игнорировать r_вых от Q₂.

Итак, нам нужна новая принципиальная схема:

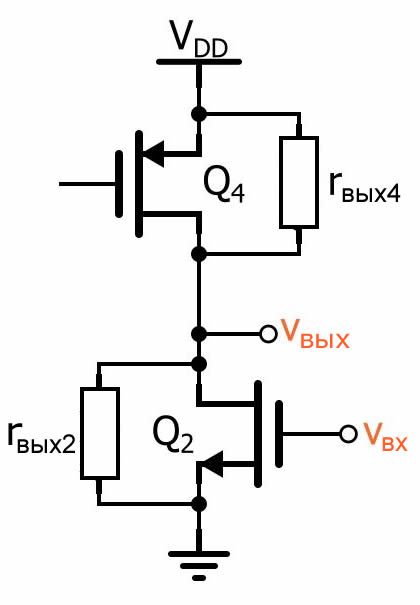
Теперь общее выходное сопротивление равно r_вых2 || r_вых4, и мы справедливо решаем, что усиление дифференциальной пары с активной нагрузкой будет равно:

\[A_{V,ан}=g_m\times \left(r_{вых4}\parallel r_{вых2}\right)\]

где g_m относится к крутизне транзисторов усилителя (Q₁ и Q₂), а не транзисторов токового зеркала (Q₃ и Q₄).

Измерение лямбды

На данный момент мы хотим спрогнозировать коэффициент усиления нашей дифференциальной пары с активной нагрузкой, но мы не можем этого сделать, потому что нам нужно знать значения r_вых4 и r_вых2.

Для этого нам нужно знать лямбду, потому что

\[r_{вых}=\frac{1}{\lambda\times I_с}\]

Я знаю, что вы думаете: просто посмотри на модель SPICE!

Увы, это не всегда так просто. Модели MOSFET, которые мы используем в наших моделированиях, имеют вид «BSIM3», что означает, что они слишком сложны для подхода к модуляции длины канала на основе лямбды. Другими словами, в модели SPICE вы не найдете лямбду, потому что она была заменена другими параметрами, которые позволяют проводить более точное моделирование.

Итак, у нас есть хорошая возможность определить лямбда эмпирически. Как мы собираемся это сделать? Рассмотрим следующий график зависимости тока стока от напряжения сток-исток:

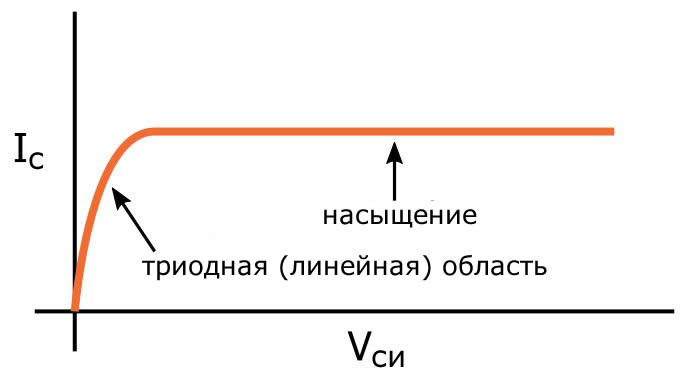
Во-первых, мы подаем достаточно высокое напряжение затвор-исток, чтобы вывести полевой транзистор из режима отсечки. Затем, удерживая V_зи постоянным, мы увеличиваем напряжение сток-исток. Когда V_си становится достаточно высоким, чтобы отсечь канал, полевой транзистор входит в режим насыщения. Если мы игнорируем модуляцию длины канала, кривая будет совершенно плоской (как показано выше), потому что увеличение V_си не влияет на ток стока.

Следующий график, напротив, не является плоским в области насыщения, потому что он включает в себя модуляцию длины канала:

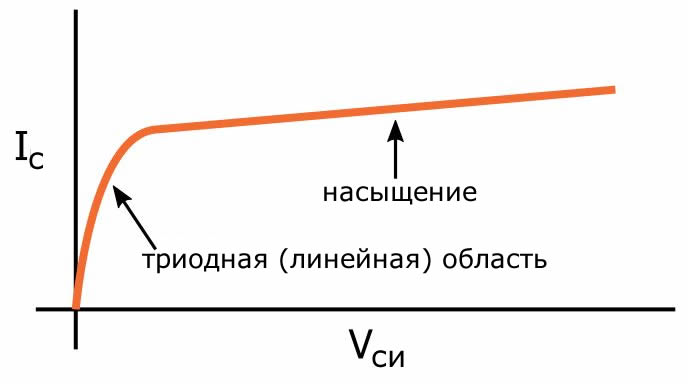
Постепенное увеличение тока стока в области насыщения соответствует дополнительному току, протекающему через выходное сопротивление при увеличении напряжения истока до истока. Если мы продолжим эту линию назад до оси x, то получим лямбду:

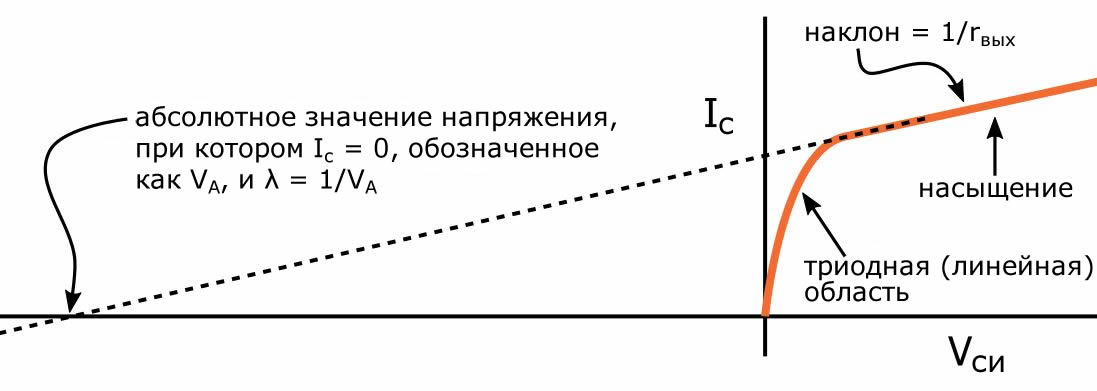
Как показано на графике, вы также можете измерить наклон и преобразовать его непосредственно в r_вых.

Моделирование лямбды

Ниже показана схема LTspice, которую я использовал для определения лямбды:

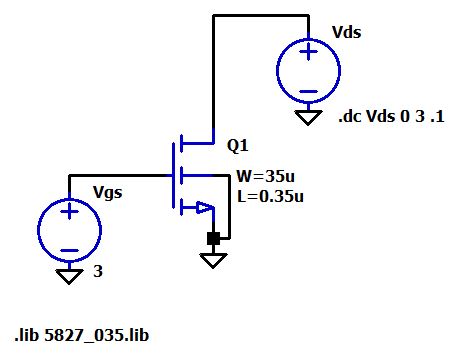
А ниже соответствующий график зависимости тока стока от напряжения сток-исток:

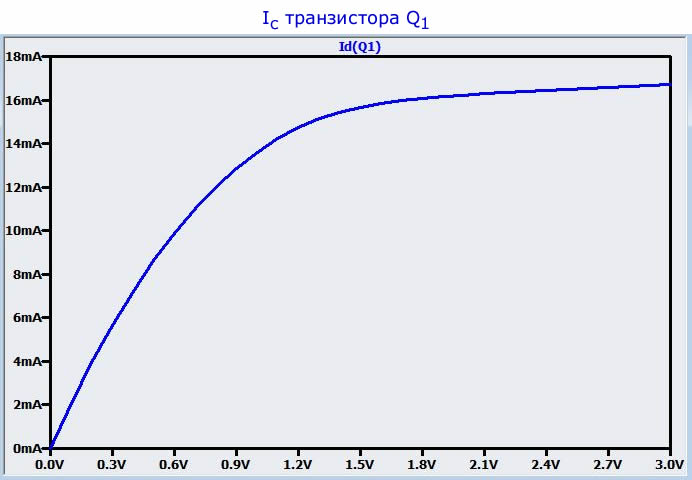
Для получения приблизительного значения лямбды мы будем использовать простой графический метод:

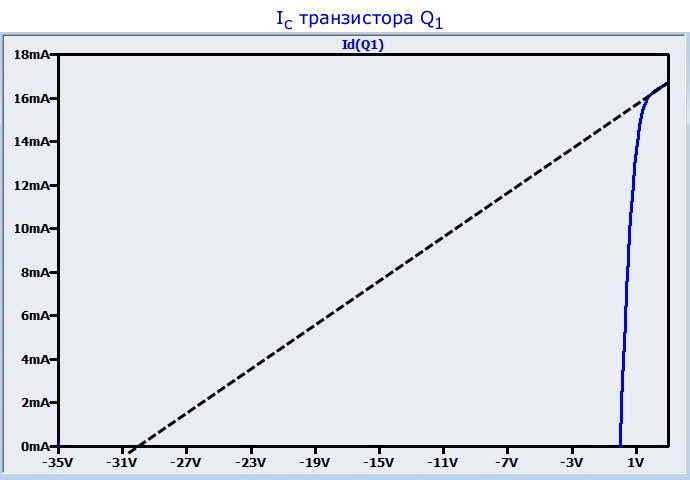
Расчет коэффициента усиления

Итак, допустим, что λ ≈ 1/(30 В) = 0,033 В^–1. В моделированиях, выполненных в предыдущей статье, мы использовали I_смещ = 500 мкА, что соответствует для Q₂ и Q₄ постоянному току стока 250 мкА.

Таким образом, мы имеем

\[r_{вых}=\frac{1}{\lambda\times I_с}=\frac{1}{0.033\ В^{-1}\times 250\ мкА}\approx 121\ кОм\]

Просто чтобы немного упростить себе жизнь, мы будем использовать это значение r_вых и для NMOS транзисторов, и для PMOS транзисторов; хотя в действительности мы не можем предположить, что λ_PMOS = λ_NMOS. Из предыдущей статьи (смотрите расчеты в конце раздела «Дифференциальное усиление») мы знаем, что g_m для наших NMOS-транзисторов составляет 0,00182 А/В. Таким образом, мы рассчитываем наш коэффициент усиления следующим образом:

\[A_{V,ан}=g_m\times (r_{вых4}\parallel r_{вых2})=0,00182\ \frac{А}{В}\times(121\ кОм \parallel 121\ кОм)\approx110\]

Я проверил это значение с помощью моделирования, и результаты даже не были близки. Промоделированный коэффициент усиления было около 22.

Конечно, обескураживает, когда моделирования не подтверждают расчеты, но в этом случае это не слишком удивительно. Напротив, расхождение значений напоминает нам, что наши упрощенные модели намного менее точны с короткими длинами канала (в моделировании я использовал 0,35 мкм). На самом деле, один из документов, который сопровождает используемые нами модели SPICE полевых транзисторов, гласит следующее: «Осторожно: не ожидайте очень точных результатов, используя ручные вычисления, особенно для коротких длин каналов (L <2 мкм)».

Хорошая новость заключается в том, что я получил гораздо лучшие результаты, когда увеличил длину канала в моделировании до 2 мкм (я также увеличил ширину канала, чтобы сохранить то же соотношение ширины к длине). В упомянутом выше документе предлагается лямбда 0,025 В^–1 для NMOS и 0,019 В^–1 для PMOS с L = 2 мкм; это дает r_вых2 = 160 кОм и r_вых4 ≈ 211 кОм, и, таким образом, A_V,ан ≈ 166. Это намного больше согласуется с моделируемым усилением, которое составило приблизительно 176.

Заключение

В этой серии статей мы подробно рассмотрели дифференциальную пару на MOSFET транзисторах с активной нагрузкой. Я надеюсь, что теперь у вас есть четкое понимание преимуществ и основных характеристик для входа-выхода этой важной схемы.

Теги