Схемы усреднителя и сумматора

Если мы возьмем три одинаковых резистора и подключим один конец каждого из них к общей точке, а затем подадим три входных напряжения (по одному на каждый из свободных концов резисторов), напряжение, наблюдаемое в общей точке, будет равно среднему арифметическому этих трех напряжений.

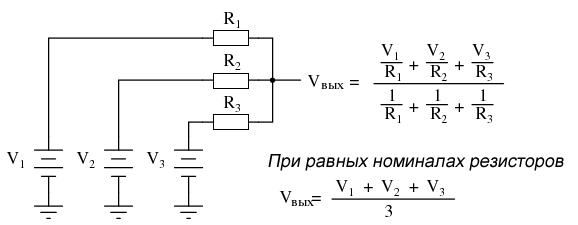
Эта схема действительно не что иное, как практическое применение теоремы Миллмана:

Эта схема широко известна как пассивный усреднитель, поскольку она создает среднее напряжение без усилительных компонентов. Пассивный просто означает, что эта схема без усиления. Большое уравнение справа от схемы усреднителя исходит из теоремы Миллмана, в которой описывается напряжение, создаваемое несколькими источниками напряжения, соединенными друг с другом через отдельные сопротивления. Поскольку три резистора в схеме усреднителя равны друг другу, мы можем упростить формулу Миллмана, записав R₁, R₂ и R₃ просто как R (одно, одинаковое сопротивление вместо трех отдельных сопротивлений):

\[V_{вых} = { {V_1 \over R} + {V_2 \over R} + {V_3 \over R} \over {1 \over R} +{1 \over R} + {1 \over R} }\]

\[V_{вых} = { {V_1 + V_2 + V_3 \over R} \over {3 \over R} }\]

\[V_{вых} = {V_1 + V_2 + V_3 \over 3 }\]

Если мы возьмем пассивный усреднитель и используем его для подключения трех входных напряжений к схеме усилителя на операционном усилителе с коэффициентом усиления 3, мы сможем превратить эту функцию усреднения в функцию сложения. Результат называется схемой неинвертирующего сумматора:

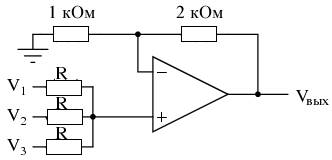
С делителем напряжения, состоящим из комбинации 2кОм/1кОм, схема неинвертирующего усилителя будет иметь коэффициент усиления по напряжению 3. Принимая напряжение от пассивного усреднителя, которое представляет собой сумму V₁, V₂ и V₃, деленную на 3, и умножая это среднее арифметическое на 3, мы приходим к выходному напряжению, равному сумме V₁, V₂ и V₃:

\[V_{вых} = 3 {V_1 + V_2 + V_3 \over 3 }\]

\[V_{вых} = V_1 + V_2 + V_3 \]

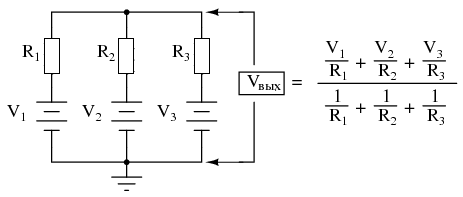
То же самое можно сделать и с инвертирующим усилителем на операционном усилителе, используя пассивный усреднитель в качестве части схемы делителя обратной связи. Результат называется схемой инвертирующего сумматора:

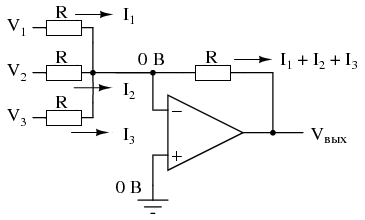
Теперь, когда правые стороны трех усредняющих резисторов соединены с точкой виртуальной земли инвертирующего входа операционного усилителя, теорема Миллмана больше не применяется так, как раньше. Напряжение на виртуальной земле теперь удерживается отрицательной обратной связью ОУ на 0 вольт, тогда как раньше оно свободно доходило до среднего значения V₁, V₂ и V₃. Однако, при всех значениях резисторов, равных друг другу, токи через каждый из трех резисторов будут пропорциональны их соответствующим входным напряжениям. Поскольку эти три тока будут складываться в узле виртуальной земли, алгебраическая сумма этих токов через резистор обратной связи будет создавать напряжение на V_вых, равное V₁ + V₂ + V₃, за исключением обратной полярности. Изменение полярности – это то, что делает эту схему инвертирующим сумматором.

\[V_{вых} = -(V_1 + V_2 + V_3 )\]

Схемы сумматоров весьма полезны дя аналогового компьютерного проектирования, так же как и схемы умножителя и делителя. Опять же, чрезвычайно высокий дифференциальный коэффициент усиления операционного усилителя позволяет нам строить эти полезные схемы с минимальным количеством компонентов.

Резюме

• Схема сумматора – это схема, которая суммирует, или складывает, несколько аналоговых сигналов напряжения вместе. Существует два основных варианта схем сумматоров на операционных усилителях: неинвертирующий и инвертирующий.

Теги