Обработка сигнала промежуточной частоты в анализаторах спектра
Обработка сигнала ПЧ выполняется на последней промежуточной частоте (в нашем примере 20,4 МГц).
Здесь сигнал снова усиливается, а ширина полосы разрешения определяется фильтром ПЧ.
Усиление на этой последней ПЧ можно регулировать с определенным шагом (в нашем примере шаг равен 0,1 дБ), поэтому при последующей обработке можно поддерживать максимальный уровень сигнала постоянным независимо от настройки аттенюатора и уровня сигнала на смесителе. При высоких значениях ослабления аттенюатора необходимо увеличить усиление сигнала ПЧ, чтобы полностью использовать динамический диапазон следующих далее в тракте детектора огибающей и аналого-цифрового преобразователя (смотрите раздел 4.6 «Зависимости между настройками»).
Фильтр ПЧ используется для определения той части входного сигнала, преобразованного на ПЧ, которая должна отображаться в определенной точке на оси частот. Из-за высокой крутизны спада и получающихся в итоге характеристик избирательности было бы желательно использовать фильтр с прямоугольной амплитудно-частотной характеристикой (АЧХ). Однако переходная характеристика таких прямоугольных фильтров не подходит для анализа спектра. Поскольку такой фильтр имеет большое время переходных процессов, спектр входного сигнала, чтобы избежать ошибок измерения уровней, можно перенести на ПЧ только путем очень медленного изменения частоты гетеродина. Короткое время измерения может быть достигнуто за счет использования фильтров Гаусса, оптимизированных относительно времени переходных процессов. Передаточная функция такого фильтра показана на рисунке 1.
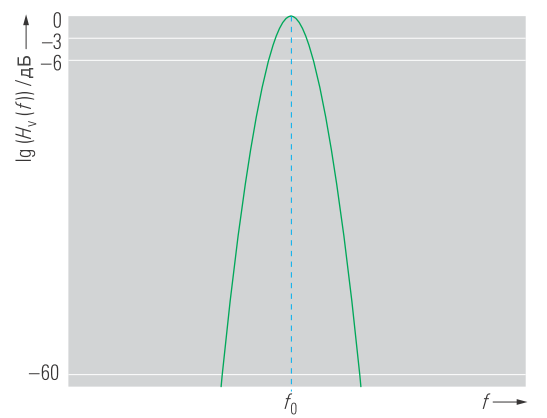
В отличие от фильтров с прямоугольной АЧХ с резким переходом от полосы пропускания к полосе задерживания, полоса пропускания гауссовых фильтров указывается с учетом ограниченной крутизны спада. В спектральном анализе обычно указывается ширина полосы по уровню 3 дБ (частотный интервал между двумя точками частотной характеристики, при котором вносимые потери фильтра увеличиваются на 3 дБ относительно центральной частоты).
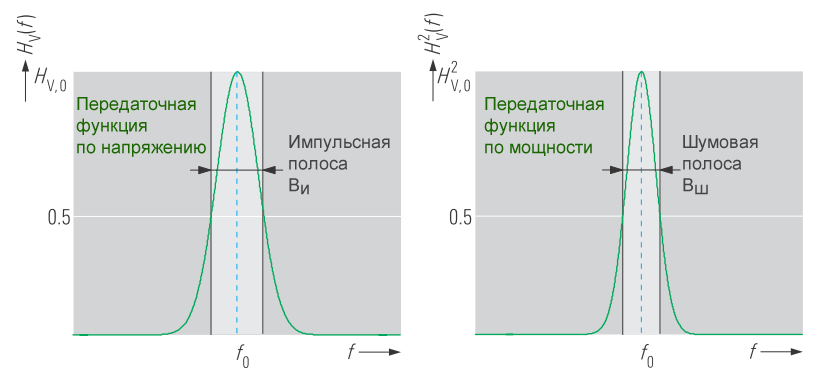
Для многих измерений шума или шумоподобных сигналов (например, сигналов с цифровой модуляцией) измеренные уровни должны быть привязаны к ширине полосы измерения, в нашем примере – к полосе разрешения. Для этого должна быть известна эквивалентная шумовая полоса Bш фильтра ПЧ, которую можно вычислить из передаточной функции следующим образом:
\[B_ш = \frac{1}{H^2_{V,0}} \cdot \int^{+\infty}_0 H^2_V(f) \cdot df \qquad (1)\]
где
- Bш – ширина шумовой полосы;
- HV(f) – передаточная функция по напряжению;
- HV,0 – значение передаточной функции по напряжению в центре полосы (при f0).
Лучше всего это можно проиллюстрировать, взглянув на передаточную функцию по мощности (рисунок 2). Ширина шумовой полосы соответствует ширине прямоугольника с той же площадью, что и площадь передаточной функции \(H^2_V(f)\). Влияние ширины полосы пропускания фильтра ПЧ подробно рассматривается в разделе 5.1 «Собственный шум».
Для измерений коррелированных сигналов, которые обычно можно найти в области использования радаров, также представляет интерес ширина импульсной полосы. В отличие от ширины шумовой полосы, ширина импульсной полосы рассчитывается путем интегрирования передаточной функции по напряжению. Применима следующая формула:
\[B_и = \frac{1}{H_{V,0}} \cdot \int^{+\infty}_0 H_V(f) \cdot df \qquad (2)\]
где
- Bи – ширина импульсной полосы;
- HV(f) – передаточная функция по напряжению;
- HV,0 – значение передаточной функции по напряжению в центре полосы (при f0).
Ширина импульсной полосы гауссовых или гауссоподобных фильтров примерно соответствует полосе пропускания по уровню 6 дБ. В области измерения помех, где часто проводятся спектральные измерения импульсов, указывается исключительно ширина полосы по уровню 6 дБ. Более подробную информацию об измерениях импульсных сигналов можно найти в разделе 6.2.
Глава 6 посвящена измерениям импульсного и фазового шума. Для этих и других измерений особый интерес представляют точные соотношения между полосами пропускания по уровням 3 дБ и 6 дБ, шумовой и импульсной полосами. В таблице 1 приведены коэффициенты преобразования для различных фильтров, которые подробно будут описаны ниже.
Таблица 1. Соотношение между ширинами полос пропускания по уровням 3 дБ и 6 дБ и ширинами шумовой и импульсной полос
| Фильтр из 4 звеньев (аналог.) | Фильтр из 5 звеньев (аналог.) | Фильтр Гаусса (цифр.) | |
|---|---|---|---|
| Исходное значение – ширина полосы по уровню 3 дБ | |||
| Ширина полосы по уровню 6 дБ (B6дБ) | 1,480 · B3дБ | 1,464 · B3дБ | 1,415 · B3дБ |
| Ширина шумовой полосы (Bш) | 1,129 · B3дБ | 1,114 · B3дБ | 1,065 · B3дБ |
| Ширина импульсной полосы (Bи) | 1,806 · B3дБ | 1,727 · B3дБ | 1,506 · B3дБ |
| Исходное значение – ширина полосы по уровню 6 дБ | |||
| Ширина полосы по уровню 3 дБ (B3дБ) | 0,676 · B6дБ | 0,683 · B6дБ | 0,707 · B6дБ |
| Ширина шумовой полосы (Bш) | 0,763 · B6дБ | 0,761 · B6дБ | 0,753 · B6дБ |
| Ширина импульсной полосы (Bи) | 1,220 · B6дБ | 1,179 · B6дБ | 1,065 · B6дБ |
Если анализатор, работающий по гетеродинному принципу, использовать для записи чисто синусоидального сигнала, в соответствии с теоремой Фурье на спектре можно ожидать появления только одной линии, даже если взять небольшую полосу обзора (SPAN) относительно частоты сигнала. Но в реальности мы получаем изображение, показанное на рисунке 3.
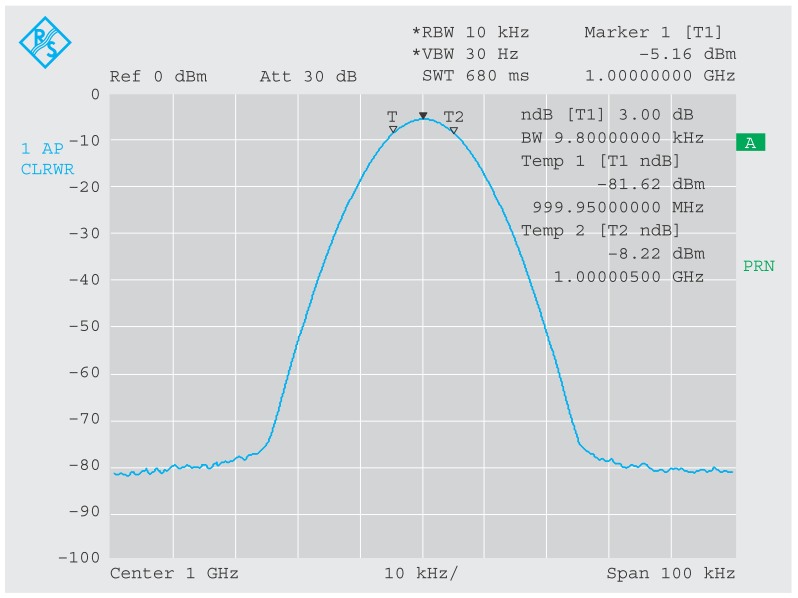
На дисплее отображается форма амплитудно-частотной характеристики фильтра ПЧ. Во время развертки входной сигнал, преобразованный в сигнал ПЧ, «сканирует через» фильтр ПЧ и умножается на его передаточную функцию.
Диаграмма этого процесса представлена на рисунке 4. Для упрощения понимания, на рисунке изображено, как фильтр «сканирует через» сигнал с фиксированной частотой, поскольку оба этих типа представления эквивалентны.
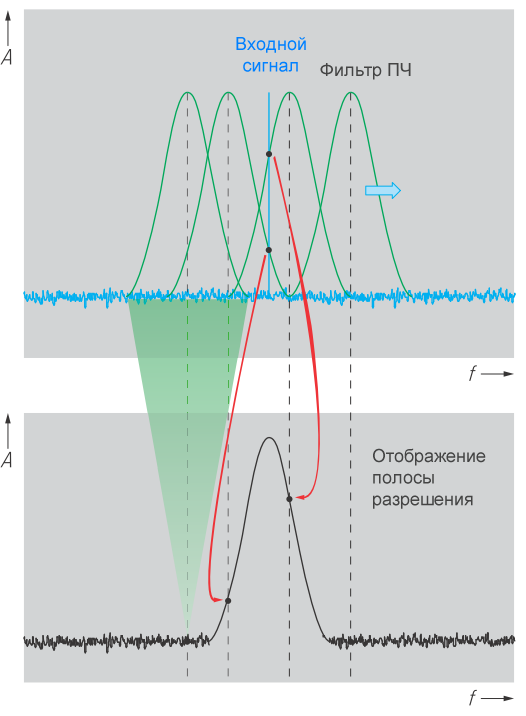
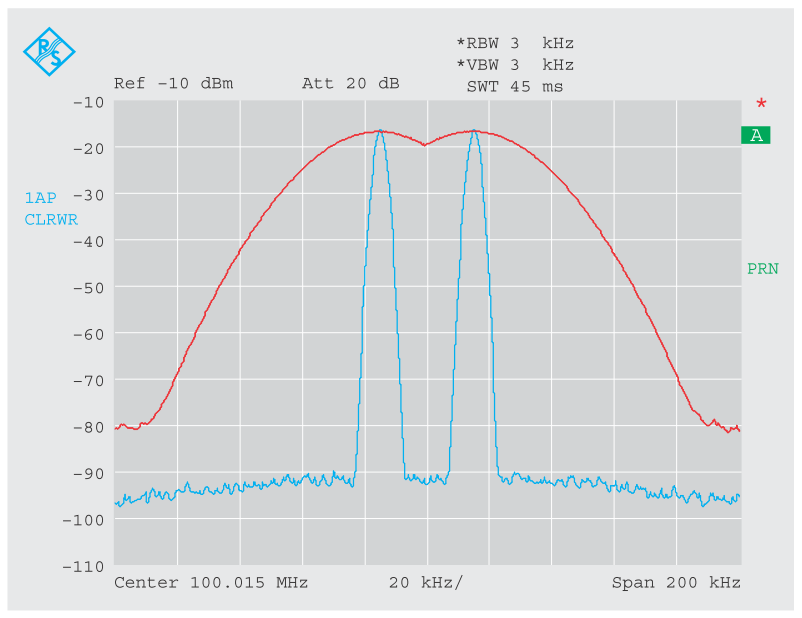
Как указывалось ранее, спектральное разрешение анализатора в основном определяется полосой разрешения, то есть полосой пропускания фильтра ПЧ. Ширина полосы фильтра ПЧ (полоса пропускания по уровню 3 дБ) соответствует минимальному смещению частоты между двумя сигналами одинакового уровня, необходимому, чтобы эти сигналы можно было различить по провалу около 3 дБ на дисплее при использовании детектора выборки или пикового детектора (смотрите раздел 4.4). Этот случай показан на рисунке 5а. Красный график был записан с полосой разрешения 30 кГц. За счет уменьшения полосы разрешения два сигнала стали четко различимы (рисунок 5a, синий график).
Если два соседних сигнала имеют явно разные уровни, то при установке слишком большой полосы разрешения более слабый сигнал не будет отображаться на выводимом спектре (рисунок 5b, красная кривая). Слабый сигнал может быть отображен на выводимом спектре при уменьшении полосы разрешения.
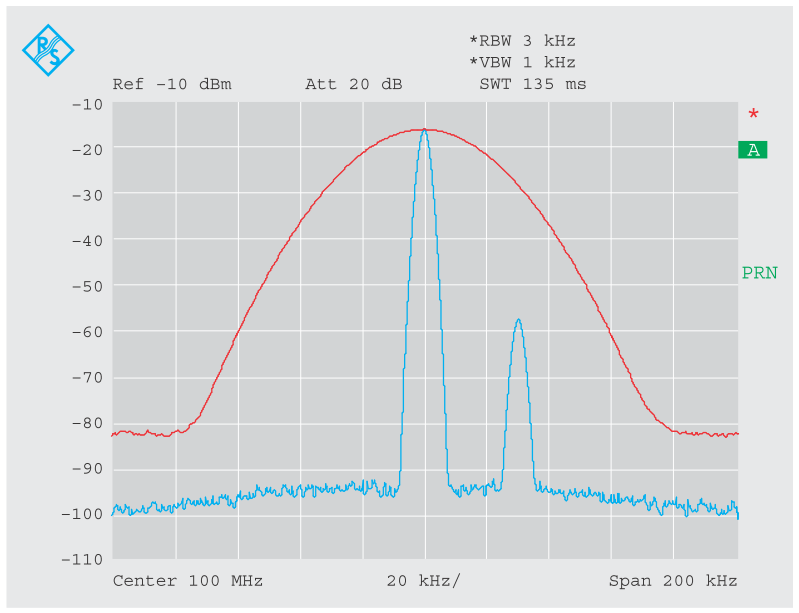
В таких случаях также важна крутизна спадов характеристики фильтра промежуточной частоты, определяющая избирательность фильтра. Крутизна спадов характеристики выражается в виде коэффициента формы (прямоугольности), который рассчитывается следующим образом:
\[КФ_{60/3} = \frac{B_{60дБ}}{B_{3дБ}} \qquad (3)\]
где
- B3дБ – полоса по уровню 3 дБ;
- B60дБ – полоса по уровню 60 дБ.
Для ширины полосы по уровню 6 дБ, принятой при измерениях электромагнитной совместимости, коэффициент форм определяется из отношения ширин полосы пропускания по уровню 60 дБ к ширине полосы пропускания по уровню 6 дБ.
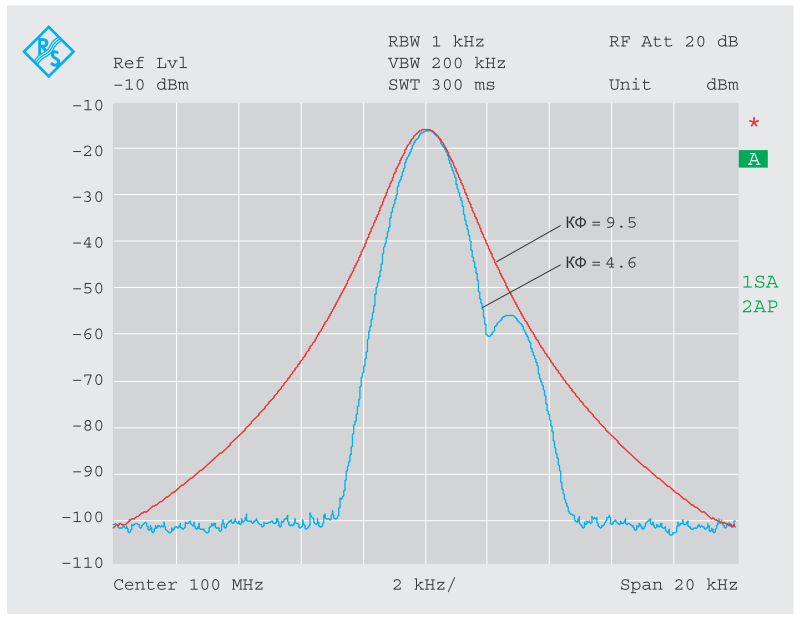
Влияние спада АЧХ ясно видно на рисунке 6. Для этих двух графиков использовались фильтры ПЧ с полосой пропускания один килогерц, но с разными коэффициентами формы. На синей кривой (КФ = 4,6) более слабый сигнал всё еще можно распознать по провалу, но на красной кривой (КФ = 9,5), где более слабый сигнал вообще не проявляется, и разделение двух сигналов невозможно.
Если более слабый сигнал должен распознаваться при использовании фильтра с низкой крутизной спада характеристики, то полосу разрешения необходимо уменьшить. Из-за большего времени переходных процессов у узкополосных фильтров ПЧ минимальное время развертки должно быть увеличено. Поэтому при использовании фильтров с высокой крутизной спада характеристики для определенных измерений возможно применение более короткого времени развертки.
Как упоминалось ранее, самое высокое разрешение достигается с помощью узкополосных фильтров ПЧ. Однако эти фильтры всегда имеют большее время переходных процессов, чем широкополосные фильтры, и поэтому современные анализаторы спектра предоставляют большое количество полос разрешения, позволяя подстроить разрешение и скорость измерения к конкретным измерениям. Диапазон перестройки обычно достаточно большой (от 10 Гц до 10 МГц). Отдельные фильтры могут быть реализованы по-разному. Существует три разных типа фильтров:
- аналоговые фильтры;
- цифровые фильтры;
- БПФ.
Аналоговые фильтры сигнала ПЧ
Аналоговые фильтры используются для реализации очень больших полос разрешения. В анализаторе спектра, описанном в нашем примере, это полосы частот от 100 кГц до 10 МГц. При использовании аналоговых фильтров идеальные фильтры Гаусса не могут быть реализованы. Однако возможно очень хорошее приближение, по крайней мере, в пределах полосы по уровню 20 дБ, поэтому переходные процессы в них почти идентичны переходным процессам гауссова фильтра. Характеристики избирательности зависят от количества звеньев в фильтре. Анализаторы спектра обычно содержат четырехзвенные фильтры, но можно найти модели и с пятизвенными фильтрами. Таким образом, можно получить коэффициенты формы около 14 и 10, тогда как идеальный фильтр Гаусса имеет коэффициент формы 4,6.
В анализаторе спектра, описанном в нашем примере, используются фильтры ПЧ, состоящие из четырех отдельных звеньев. Фильтрация распределена так, что по два звена фильтра (29 и 31) расположены до и после усилителя ПЧ 30. Эта конфигурация предлагает следующие преимущества:
- фильтр перед усилителем ПЧ обеспечивает подавление продуктов преобразования за пределами полосы пропускания фильтра ПЧ. Таким образом, можно избежать продуктов интермодуляции, которые без выполнения предварительной фильтрации могут быть вызваны этими сигналами в последнем усилителе ПЧ (смотрите раздел 5.2 «Нелинейности»).
- фильтр после усилителя ПЧ используется для уменьшения ширины шумовой полосы. Если бы он был расположен перед усилителем ПЧ, общая мощность шума при последующем детектировании огибающей была бы заметно выше из-за широкополосного шума усилителя ПЧ.
Цифровые фильтры сигнала ПЧ
Узкую полосу пропускания лучше всего реализовать с помощью цифровой обработки сигналов. В отличие от аналоговых фильтров, в этом случае могут быть реализованы идеальные гауссовы фильтры. Используя цифровые фильтры вместо аналоговых, можно добиться гораздо лучшей избирательности при сохранении приемлемой стоимости схемы. Например, аналоговые фильтры, состоящие из пяти отдельных звеньев, имеют коэффициент формы около 10, тогда как идеальный гауссовский фильтр, реализованный в цифровой форме, имеет коэффициент формы 4,6. Кроме того, цифровые фильтры обладают температурной стабильностью, не подвержены эффектам старения и не требуют настройки. Поэтому они имеют более высокую точность относительно полосы пропускания.
Переходные процессы цифровых фильтров определяемы и известны. При использовании соответствующих поправочных коэффициентов цифровые фильтры обеспечивают более короткое время развертки, по сравнению с аналоговыми фильтрами той же ширины полосы (смотрите раздел 4.6 «Зависимости между настройками»).
В отличие от реализации, показанной на структурной схеме, сигнал ПЧ после усилителя ПЧ сначала должен быть оцифрован с помощью аналого-цифрового преобразователя. Чтобы соответствовать теореме о дискретизации, ширина полосы сигнала ПЧ перед дискретизацией должна быть предварительно ограничена аналоговыми фильтрами. Это ограничение полосы происходит перед усилителем ПЧ, чтобы можно было избежать продуктов интермодуляции, как это было в случае аналоговых фильтров. Полоса пропускания предварительного фильтра изменяема, поэтому в зависимости от установленной цифровой полосы разрешения можно выбрать минимально возможную полосу пропускания этого предварительного фильтра. Цифровой фильтр ПЧ позволяет ограничить шумовую полосу до выполнения детектирования огибающей.
Цифровой фильтр ПЧ может быть реализован с помощью конфигураций, описанных в [1] или [2]. В нашем примере полосы разрешения от 10 Гц до 30 кГц анализатора спектра реализованы с помощью цифровых фильтров.
БПФ
Очень узкая полоса пропускания фильтра ПЧ приводит к длительным переходным процессам, что значительно уменьшает допустимую скорость развертки. Поэтому при очень высоком разрешении рекомендуется рассчитывать спектр на основе временной характеристики – аналогично БПФ анализатору, описанному в разделе 3.1 «БПФ-анализатор (анализатор спектра на основе быстрого преобразования Фурье)». Поскольку очень высокочастотные сигналы (до нескольких ГГц) не могут быть напрямую оцифрованы с помощью АЦП, то необходимый пользователю частотный диапазон переносится на ПЧ целиком с помощью сигнала гетеродина фиксированной частоты, и пропущенный сигнал оцифровывается во временной области (рисунок 7). Для обеспечения однозначности в этом случае требуется предварительный аналоговый фильтр.
Для сигнала ПЧ с центральной частотой fпч и шириной полосы B в соответствии с теоремой дискретизации (уравнение 1 в разделе 3.1 «БПФ-анализатор») можно определить минимальную частоту дискретизации 2·(fпч+0,5·B). Однако, если относительная ширина полосы сигнала мала (B/fпч << 1), то допустима субдискретизация. То есть частота дискретизации может быть ниже, чем частота дискретизации, полученная в результате теоремы Найквиста-Шеннона-Котельникова для сигналов основной полосы частот (низкочастотных сигналов). Чтобы гарантировать однозначность, необходимо соблюдать теорему дискретизации для узкополосных сигналов. Допустимые частоты дискретизации определяются следующим образом:
\[\frac{2 \cdot f_{пч} + B}{k+1} \le f_s \le \frac{2 \cdot f_{пч} - B}{k} \qquad (4)\]
где
- fs – частота дискретизации;
- fпч – промежуточная частота;
- B – ширина полосы сигнала ПЧ;
- k = 1, 2, ...
Спектр может быть определен из значений выборок с помощью преобразования Фурье.
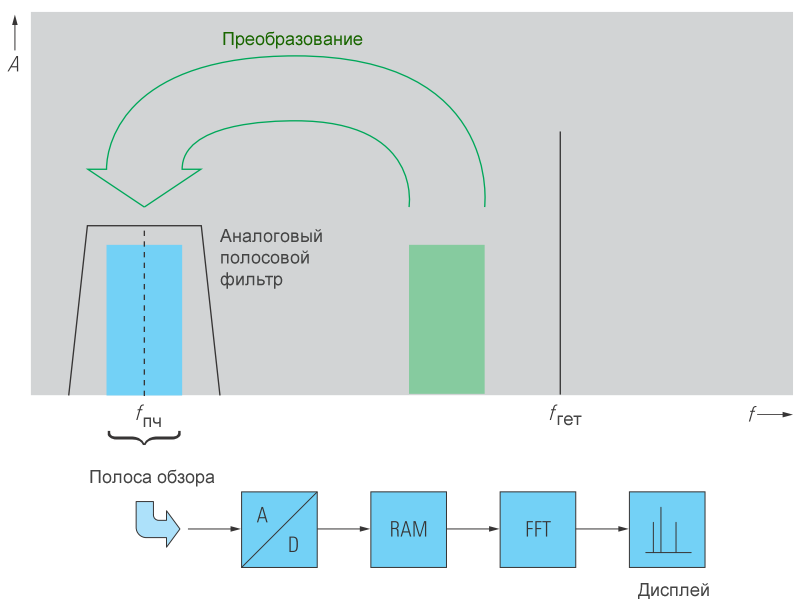
Максимальная полоса обзора (SPAN), которая может быть проанализирована с помощью БПФ при определенном разрешении, ограничена частотой дискретизации аналого-цифрового преобразователя и объемом памяти, доступной для сохранения дискретных значений. Поэтому большие полосы обзора должны быть разделены на отдельные сегменты, которые затем преобразуются на ПЧ и оцифровываются.
В то время как время развертки аналогового или цифрового фильтра увеличивается прямо пропорционально полосе обзора, время наблюдения, необходимое для БПФ, зависит от необходимого разрешения по частоте, как описано в разделе 3.1. Чтобы соответствовать требованиям к выборкам, при увеличении полосы обзора необходимо записывать больше выборок для БПФ, соответственно время вычисления для БПФ также увеличивается. При достаточно высокой скорости вычислений цифровой обработки сигналов с помощью БПФ может быть достигнуто значительно более короткое время измерения, по сравнению с обычными фильтрами, особенно при высоких отношениях полосы обзора к RBW (смотрите раздел 4.6 «Зависимости между настройками»).
Избирательность фильтров БПФ при большой расстройке ограничена эффектом растекания, зависящим от используемой оконной функции. Окно Ханна, описанное в разделе 3.1, не подходит для анализа спектра из-за амплитудных потерь и получающейся в результате ошибки определения уровня. Поэтому часто используется окно с плоской вершиной, чтобы уменьшить эффект растекания, чтобы можно было сохранить ошибку определения амплитуды на незначительном уровне. Это происходит за счет времени наблюдения, которое в 3,8 раза больше, чем у прямоугольного окна. Окно с плоской вершиной использует более широкий класс оконных функций в частотной области (соответствующих свертке с дельта-функцией Дирака в частотной области). Когда используется окно с плоской вершиной, можно получить коэффициент формы около 2,6, что означает явно лучшую избирательность, чем при использовании аналоговых или цифровых фильтров ПЧ.
Фильтры БПФ не подходят для анализа импульсных сигналов (смотрите раздел 3.1). Поэтому важно, чтобы анализаторы спектра были оснащены как фильтрами БПФ, так и обычными фильтрами.
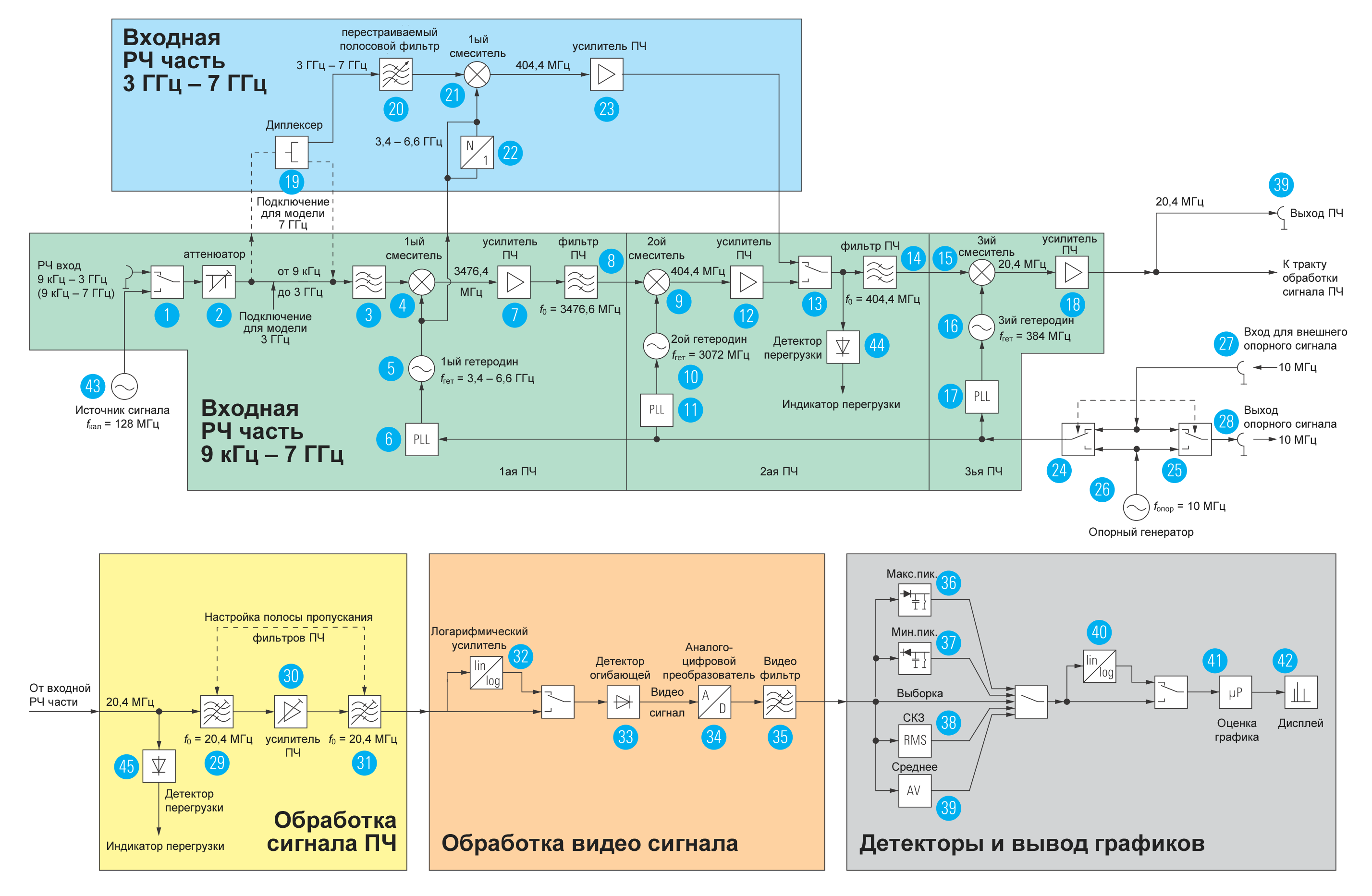
Структурная схема анализатора спектра, описываемого в данной книге
Справочная информация
- Parks, T.W., Burrus, C.S.: Digital Filter Design. John Wiley & Sons, Inc., New York, Chichester, Brisbane, Toronto, Singapore, 1987.
- Oppenheim, A.V., Schafer, R.W.: Discrete-Time Signal Processing. Prentice Hall, 1989.
