БПФ-анализатор (анализатор спектра на основе быстрого преобразования Фурье)

В зависимости от типа измерения к максимальной входной частоте анализатора спектра могут предъявляться разные требования. Принимая во внимание различные возможные конфигурации анализаторов спектра, диапазоны входных частот можно разделить следующим образом:

• низкочастотный диапазон (AF) – до приблизительно 1 МГц;
• радиочастотный диапазон (RF) – до приблизительно 3 ГГц;
• диапазон СВЧ – до приблизительно 40 ГГц;
• миллиметровый диапазон – выше 40 ГГц

Диапазон AF (до приблизительно 1 МГц) охватывает низкочастотную электронику, а также аудиотехнику и механику. В радиочастотном диапазоне в основном используются приложения беспроводной связи, такие как мобильная связь, звуковое и телевизионное вещание, в то время как более высокие диапазоны частот (сантиметровые и миллиметровые волны) всё больше используются для широкополосных приложений, таких как каналы цифровой радиосвязи.

В зависимости частотного диапазона анализаторы могут быть построены по той или иной концепции. В следующих разделах подробно описаны две основные концепции построения анализаторов спектра.

БПФ-анализатор (анализатор спектра на основе быстрого преобразования Фурье)

Как объяснялось в главе 2, частотный спектр сигнала определяется его временной характеристикой. Временная и частотная области связаны друг с другом посредством преобразования Фурье. Таким образом, уравнение 1 можно использовать для вычисления спектра сигнала, записанного во временной области. Для точного вычисления частотного спектра входного сигнала потребуется бесконечный период наблюдения. Еще одним предварительным условием уравнения 1 является то, что в каждый момент времени должна быть известна амплитуда сигнала. Результатом этого расчета будет непрерывный спектр, и поэтому разрешение по частоте будет неограниченным.

Очевидно, что такие точные вычисления на практике невозможны. Тем не менее, при определенных условиях спектр может быть определен с достаточной точностью.

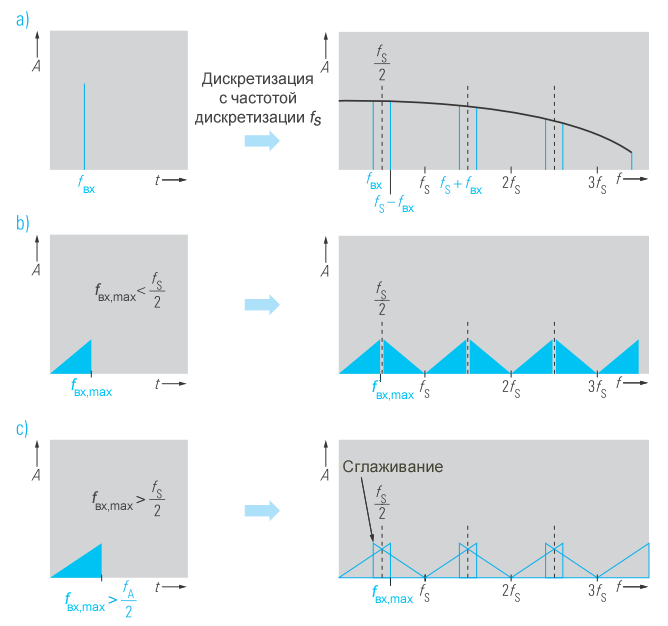
На практике преобразование Фурье выполняется с помощью цифровой обработки сигналов, поэтому анализируемый сигнал должен быть подвергнут дискретизации по времени и квантованию по амплитуде аналого-цифровым преобразователем. Посредством дискретизации непрерывный входной сигнал преобразуется в дискретный по времени сигнал, и информация о временной характеристике теряется. Следовательно, ширина полосы входного сигнала должна быть ограничена, иначе из-за дискретизации более высокие частоты сигнала вызовут эффекты наложения спектров (смотрите рисунок 1). Согласно теореме Найквиста-Шеннона-Котельникова о дискретизации, частота дискретизации f_s должна быть как минимум вдвое выше, чем ширина полосы B_вх входного сигнала:

\[f_s \ge 2 \cdot B_{вх} \qquad (1)\]

\[f_s = \frac{1}{T_s}\]

где

• f_s – частота дискретизации;
• B_вх – ширина полосы сигнала;
• T_s – период дискретизации.

Для дискретизации сигналов, прошедших фильтр нижних частот (называемых низкочастотными сигналами), минимальная необходимая частота дискретизации определяется максимальной частотой сигнала f_вх,max. Уравнение 1 преобразуется в следующее:

\[f_s \ge 2 \cdot f_{вх,max} \qquad (2)\]

Если \(f_s = 2 \cdot f_{вх,max}\), возможно, что из-за неблагоприятных условий выборки будет невозможно восстановить сигнал из значений выборок. Более того, в этом случае для ограничения полосы потребовался бы фильтр нижних частот с бесконечной крутизной характеристики. Поэтому на практике используются частоты дискретизации, намного превышающие 2f_вх,max.

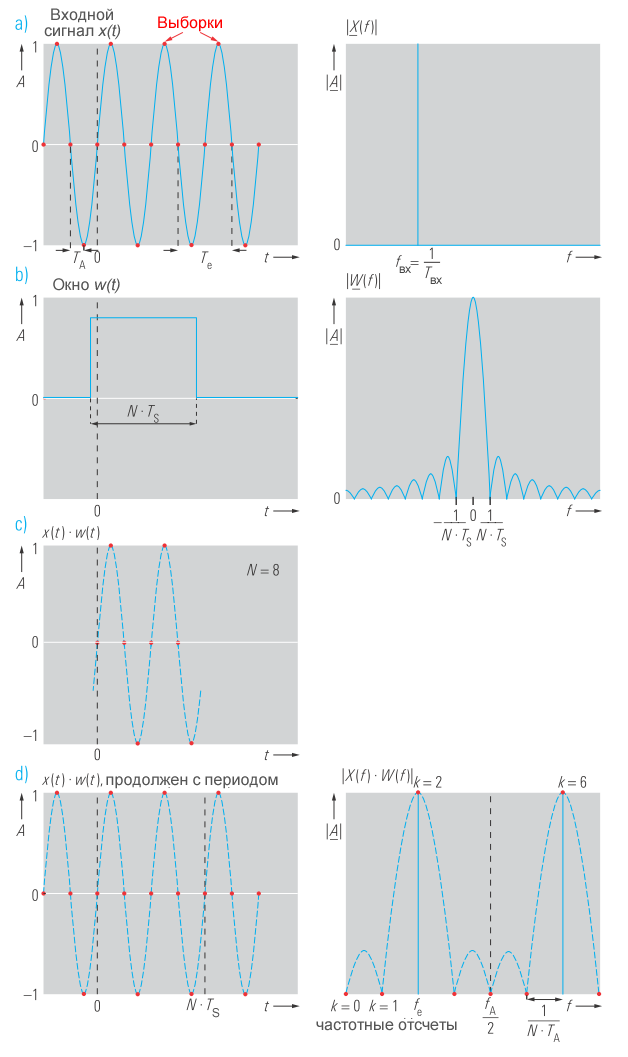
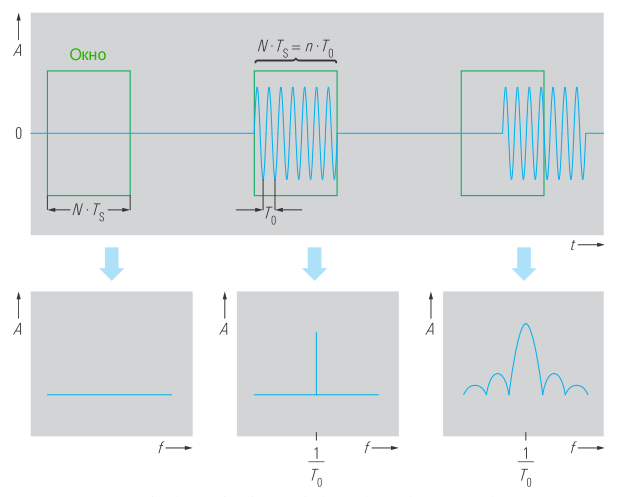
Для преобразования Фурье используется только часть сигнала. То есть для расчета используется только ограниченное количество выборок, N. Этот процесс называется «оконной обработкой». Входной сигнал (рисунок 2a) умножается на определенную оконную функцию до или после дискретизации во временной области. В примере, показанном на рисунке 2, используется прямоугольное окно (рисунок 2b). Результат умножения показан на рисунке 2c.

Вычисление спектра сигнала из выборок сигнала во временной области называется дискретным преобразованием Фурье (ДПФ).

Уравнение 1 преобразуется в следующее:

\[X(k) = \sum^{N-1}_{n=0} x(nT_s) \cdot e^{-j2\pi kn/N} \qquad (3)\]

где

• k – номер частотного отсчета, где k = 0, 1, 2, ...;
• n – номер временного отсчета;
• x(nT_s) – выборки в точке n·Ts, где n = 0, 1, 2, ...;
• N – длина ДПФ, т.е. общее количество выборок, используемых для вычисления преобразования Фурье.

Результатом дискретного преобразования Фурье является дискретный частотный спектр (рисунок 2d). Вычисленный спектр состоит из отдельных компонентов, соответствующих отдельным частотам, которые вычисляются как:

\[f(k) = k \cdot \frac{f_s}{N} = k \cdot \frac{1}{N \cdot T_s} \qquad (4)\]

где

• f(k) – дискретный частотный компонент;
• k – номер дискретного частотного компонента, где k = 0, 1, 2, …;
• f_s – частота дискретизации;
• N – длина дискретного преобразования Фурье.

Можно видеть, что разрешение (минимальный интервал между двумя спектральными соседними компонентами входного сигнала, f(k) и f(k+1), который может быть отображен) зависит от времени наблюдения N·T_s. По мере увеличения необходимого разрешения увеличивается и требуемое время наблюдения.

При дискретизации спектр сигнала становится периодическим с периодом f_s (рисунок 1). Следовательно, на дискретном частотном спектре на рисунке 2d частотный компонент отображается на частотном отсчете f(k=6). При рассмотрении частотного диапазона от 0 до f_s на рисунке 1a становится очевидным, что этот компонент находится на частоте f_s – f_вх.

В примере, показанном на рисунке 2, возможно точное вычисление спектра сигнала. В дискретном частотном спектре есть частотный отсчет, который точно соответствует частоте сигнала. Для этого должны быть выполнены следующие требования:

• сигнал должен быть периодическим (период T₀);
• время наблюдения N·T_s должно быть целым числом, кратным периоду T₀ сигнала.

На практике эти требования обычно не выполняются, поэтому результат преобразования Фурье отличается от ожидаемого. Это отклонение характеризуется более широким спектром сигнала и ошибкой в амплитуде. Оба эффекта описаны ниже.

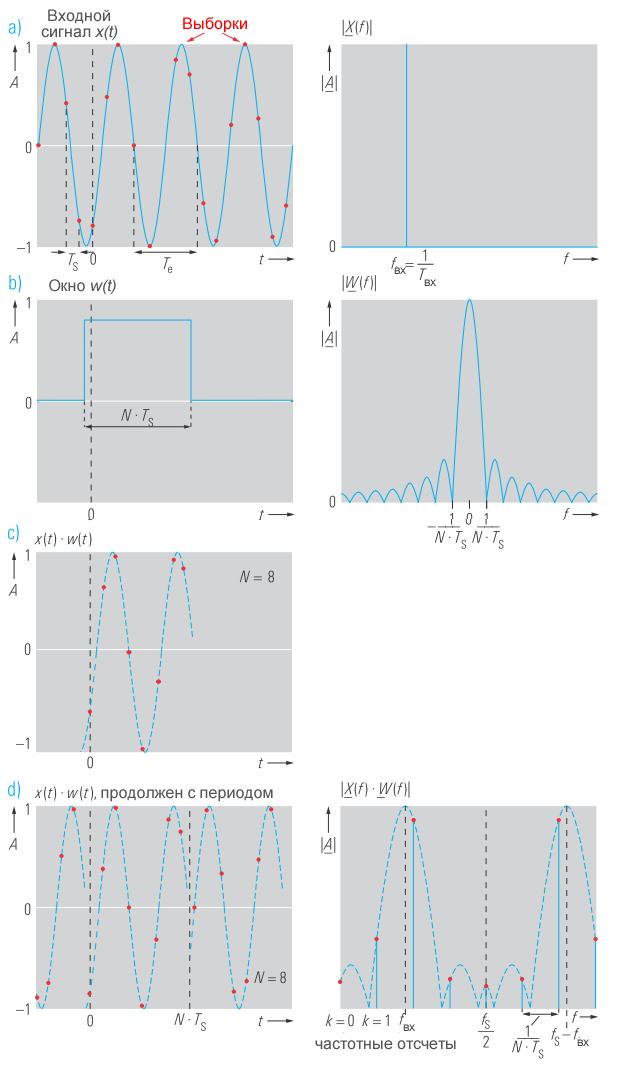
Перемножение входного сигнала и оконной функции во временной области соответствует свертке в частотной области [1]. В частотной области величина передаточной функции прямоугольного окна, показанного на рисунке 2, приводит к синусоидальной оконной функции:

\[|W(f)| = N \cdot T_s \cdot \sin(2\pi f \cdot N \cdot T_s/2) = N \cdot T_s {\sin(2\pi f \cdot N \cdot T_s/2) \over 2\pi f \cdot N \cdot T_s/2} \qquad (5)\]

где

• W(f) – оконная функция в частотной области;
• N·T_s – ширина окна

В дополнение к отчетливым вторичным максимумам, нулевые значения получаются кратными 1/(N·T_s). Из-за свертки с помощью оконной функции результирующий спектр сигнала «размывается», и поэтому он становится заметно шире. Это называется эффектом растекания спектра.

Если входной сигнал периодический, а время наблюдения N·T_s является целым кратным периоду, эффект растекания при прямоугольном окне отсутствует, поскольку, за исключением частоты сигнала, нули всегда попадают в соседние частотные отсчеты (рисунок 2d).

Если эти условия не выполняются, что является обычным случаем, то частотный отсчет, соответствующий частоте сигнала, отсутствует. Этот случай показан на рисунке 3. Спектр, полученный в результате дискретного преобразования, заметно шире, поскольку фактическая частота сигнала находится между двумя частотными отсчетами, а нули оконной функции больше не попадают в соседние частотные отсчеты.

Как показано на рисунке 3d, в этом случае также возникает ошибка в амплитуде. При постоянном времени наблюдения величина этой ошибки в амплитуде зависит от частоты входного сигнала (рисунок 4). Ошибка будет максимальна, если частота сигнала находится точно между двумя частотными отсчетами.

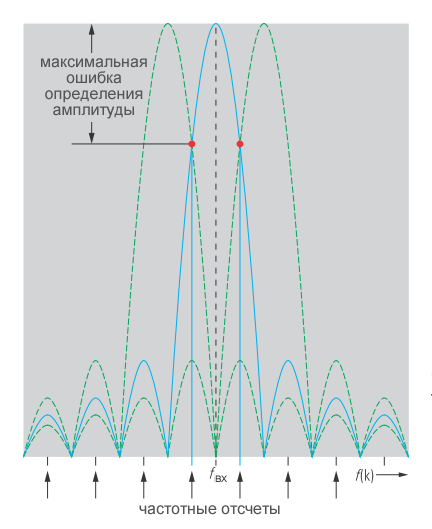
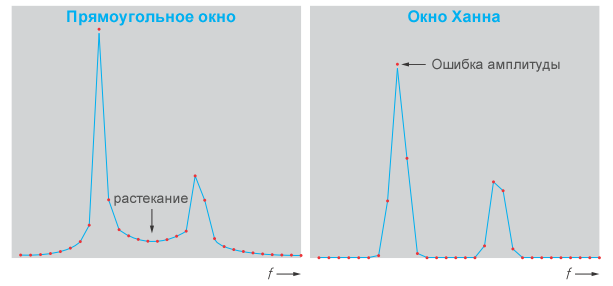
Увеличивая время наблюдения, можно уменьшить абсолютное расширение спектра за счет более высокого разрешения, но максимально возможная ошибка амплитуды остается неизменной. Однако эти два эффекта можно уменьшить, используя вместо прямоугольного окна оптимизированную оконную обработку. Такие оконные функции показывают более низкие вторичные максимумы в частотной области, и поэтому эффект растекания уменьшается, как показано на рисунке 5. Дополнительную информацию об оконных функциях можно найти в [2] и [3].

Для получения высокой точности, необходимой для спектрального анализа, обычно используется окно с плоской вершиной (flat top window). Максимальная ошибка по амплитуде этой оконной функции составляет всего 0,05 дБ. Ее недостатком является относительно широкий главный лепесток, который снижает разрешение по частоте.

Количество вычислительных операций, необходимых для преобразования Фурье, может быть уменьшено с помощью оптимизированных алгоритмов. Наиболее широко используемый метод – быстрое преобразование Фурье (БПФ, FFT). Анализаторы спектра, работающие на этом принципе, называются БПФ-анализаторами. Структурная схема такого анализатора показана на рисунке 6.

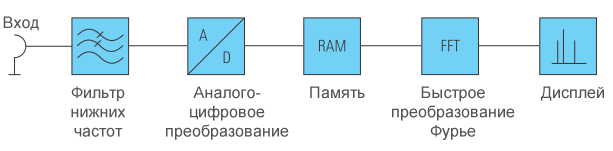
Чтобы придерживаться теоремы о дискретизации, ширина полосы входного сигнала ограничивается аналоговым фильтром нижних частот (частота среза f_ср = f_вх,max) перед аналого-цифровым преобразователем. После дискретизации квантованные значения сохраняются в памяти, а затем используются для вычисления сигнала в частотной области. И в конце частотный спектр отображается на дисплее.

Квантование выборок вызывает шум квантования, который вызывает ограничение динамического диапазона в сторону его нижнего предела. Чем выше разрешение (количество бит) используемого аналого-цифрового преобразователя, тем ниже шум квантования.

Поскольку у доступных аналого-цифровых преобразователей высокого разрешения полоса пропускания ограничена, для БПФ-анализаторов необходимо искать компромисс между динамическим диапазоном и максимальной входной частотой. В настоящее время широкий динамический диапазон около 100 дБ может быть достигнут у БПФ-анализаторов только для низкочастотных приложений до 100 кГц. Более высокая полоса пропускания неизбежно ведет к меньшему динамическому диапазону.

В отличие от других концепций построения анализаторов, во время сложного преобразования Фурье фазовая информация о сигнале не теряется. Таким образом, БПФ-анализаторы могут определять комплексный спектр, т.е. содержащий информацию и об амплитуде, и о фазе. Если они обладают достаточно высокой скоростью вычислений, то они позволяют проводить анализ даже в реальном времени.

БПФ-анализаторы не подходят для анализа импульсных сигналов (рисунок 7). Результат быстрого преобразования Фурье зависит от выбранного участка временной функции. Поэтому для правильного анализа необходимо знать некоторые параметры анализируемого сигнала для запуска конкретного измерения.

Справочная информация

1. Brigham, E.O.: The Fast Fourier Transform and its Application. Prentice Hall, 1988.
2. Parks, T.W., Burrus, C.S.: Digital Filter Design. John Wiley & Sons, Inc., New York, Chichester, Brisbane, Toronto, Singapore, 1987.
3. Oppenheim, A.V., Schafer, R.W.: Discrete-Time Signal Processing. Prentice Hall, 1989.

Теги