Умножение частоты с помощью ФАПЧ: переходная характеристика и синтез частот
Влияет ли добавление делителя частоты в обратную связь на переходной процесс системы фазовой автоподстройки частоты (ФАПЧ, PLL, phase-locked loop)? В данной статье мы рассмотрим этот вопрос, а также другие темы умножения частоты.
Вспомогательная информация
В предыдущей статье об умножении частоты мы видели, что система с фазовой автоподстройкой частоты может генерировать выходной сигнал с частотой, которая выше частоты входного (опорного) сигнала. Это достигается включением делителя частоты в петлю обратной связи.
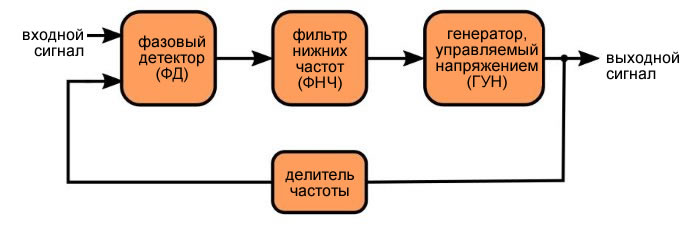
Этот высокочастотный сигнал «наследует» от входного сигнала необходимые характеристики (то есть точность и стабильность частоты во времени и температуре). Следовательно, низкокачественный генератор, управляемый напряжением, в сочетании с высококачественным (но низкочастотным) опорным сигналом может создавать высококачественный высокочастотный сигнал.
Возвращение к переходному процессу
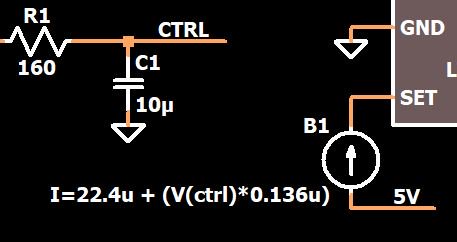
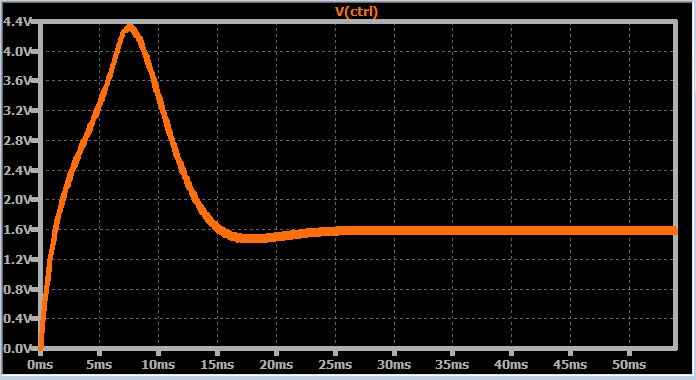
Мы уже обсуждали переходной процесс системы ФАПЧ, и, более конкретно, как разработать систему ФАПЧ с необходимым коэффициентом демпфирования (затухания колебаний). На следующем графике приведен пример управляющего напряжения ФАПЧ, которое быстро и плавно устанавливается на конечном значении:
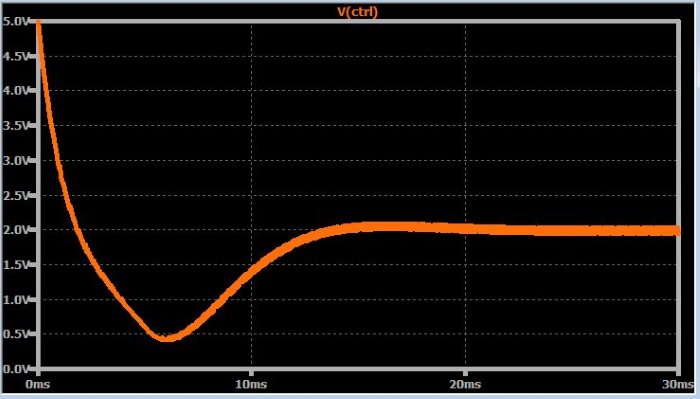
На следующем графике показано управляющее напряжение для точно такой же цели, за исключением того, что я добавил в петлю обратной связи счетчик деления на два.
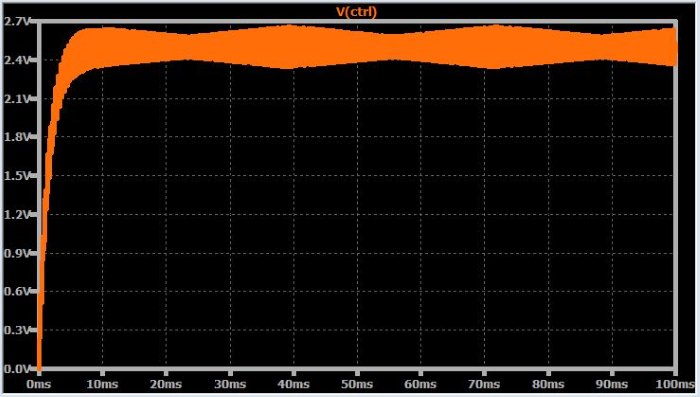
Это не выглядит ужасно, но что-то определенно изменилось. Кроме того, управляющее напряжение не достигает стабильного состояния – вы можете видеть периодические изменения на пульсирующей амплитуде.
Если мы увеличим масштаб и посмотрим на входной и выходной сигналы, станет ясно, что у нас есть более серьезная проблема:
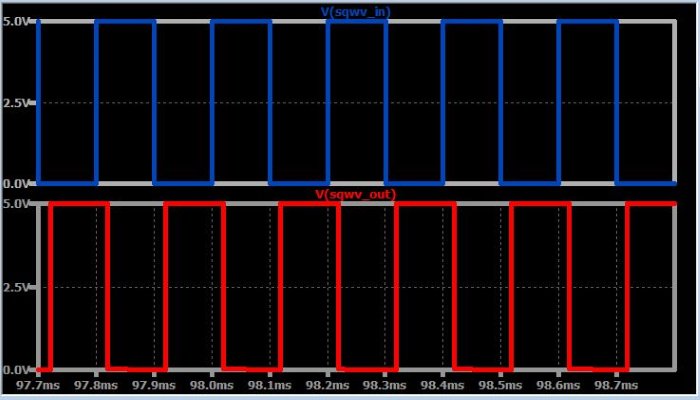
Выходная частота (fвых) определенно не в два раза больше входной частоты (fвх). Проблема здесь в том, что начальный управляющий ток ГУН не достаточно близок к 2fвх; другими словами, управляющее напряжение не может регулировать частоту ГУН на всём пути до 2fвх.
Итак, первое, что нам нужно сделать, это удвоить смещение источника тока; это приведет к тому, что начальный управляющий ток достигнет значения, при котором создается fвых, которая находится вблизи fвх.

Как показывают следующие два графика, система ФАПЧ теперь работает довольно хорошо. Переходной процесс показывает хорошее демпфирование (затухание колебаний), и fвых=2fвх.
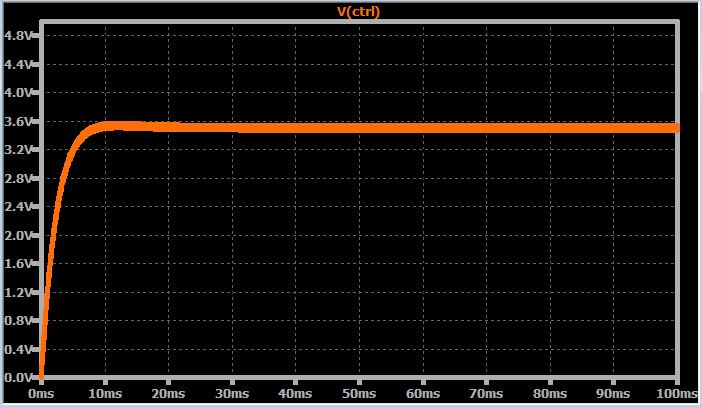
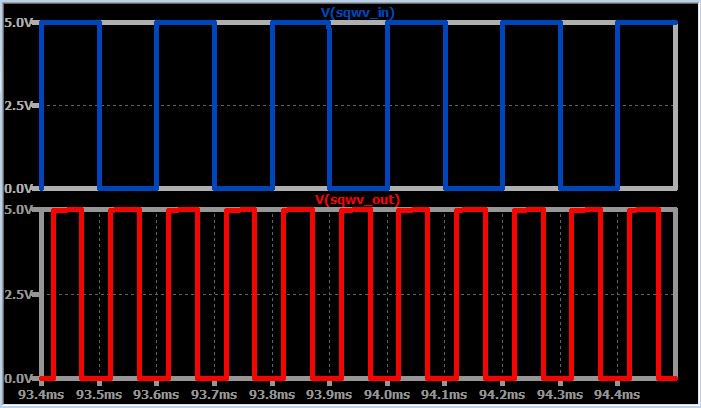
Умножение частоты, коэффициент умножения
К сожалению, этот последний набор симуляций обманул нас. ФАПЧ работает хорошо, да, но это только потому, что коэффициент умножения (обозначается как N) очень низок. Когда N = 2, переходной процесс всё еще довольно хорош, но если мы добавим больше счетчиков деления на два, чтобы получился N = 8, то обнаружится скрытая проблема:
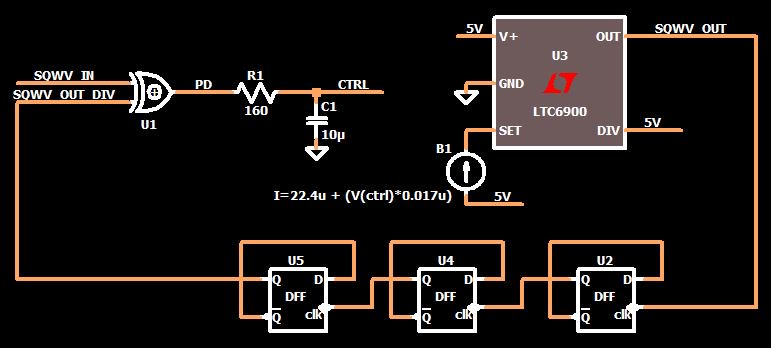
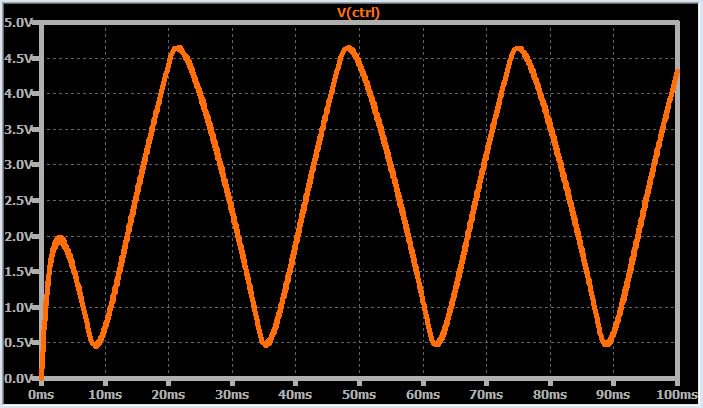
Это определенно не то, что я бы назвал серьезно затухающим переходным процессом. На самом деле, похоже, что ФАПЧ никогда не достигнет синхронизации. Это, правда, не удивительно, если мы сделаем шаг назад и подумаем о влиянии делителя частоты. Из предыдущих статей мы знаем, что на коэффициент затухания влияет K, который я описал как общий коэффициент усиления системы, то есть коэффициент усиления фазового детектора, умноженный на коэффициент усиления ГУН. Но более точное описание K – это коэффициент усиления «петли», и путь обратной связи, конечно, является частью петли.
В базовой системе ФАПЧ путь обратной связи не влияет на K, потому что это просто прямое соединение; таким образом, K = KФД × KГУН. Но теперь в пути обратной связи у нас есть делитель частоты, поэтому общий коэффициент усиления становится равным:
\[K=\frac{K_{ФД}\times K_{ГУН}}{N}\]
Суть в том, что у нас больше нет хорошего коэффициента затухания (демпфирования), потому что изменился коэффициент усиления петли. К счастью, решение простое: мы умножаем коэффициент усиления ГУН (или ФД) на N, чтобы компенсировать деление на N. Как вы можете видеть на новом графике управляющего напряжения, необходимый переходной процесс был восстановлен.
Гибкость относительно частоты
На данный момент, у нас есть хорошая идея о том, как, используя ФАПЧ, умножить входную частоту, и как изменить схему так, чтобы «коэффициент усиления» по частоте не испортил бы наш переходной процесс. Однако пока функциональность схемы несколько ограничена.
Допустим, мы потратили хорошие деньги на очень качественный кварцевый генератор с тактовой частотой 1 МГц, а затем занялись разработкой потрясающей системы ФАПЧ, чтобы смочь генерировать различные частоты из этого опорного тактового сигнала. Однако при наличии только делителя в пути обратной связи частотные параметры будут довольно ограничены: 2 МГц, 3 МГц, 4 МГц и так далее. И, фактически, если мы реализуем деление с помощью каскадно включенных триггеров, делящих на два, мы будем ограничены: 2 МГц, 4 МГц, 8 МГц и так далее.
В некоторых приложениях это может быть приемлемо, но если вы хотите большей гибкости, вы можете включить делитель частоты перед фазовым детектором:
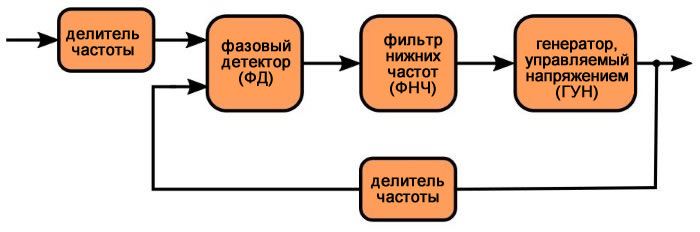
Теперь у нас есть Nвход и Nобратная связь. Входная частота системы ФАПЧ становится равной fопорная/Nвход, а затем эта частота умножается на Nобратная связь. Таким образом,
\[f_{OUT}=\frac{f_{опорная}}{N_{вход}}\times N_{обратная \ связь}=f_{опорная}\times\frac{N_{обратная \ связь}}{N_{вход}}\]
Как видите, теперь у нас есть возможность умножать опорную частоту на дробные значения, а не только на целые числа.
Возможно, вы слышали термин «система ФАПЧ с дробным N», и было бы вполне понятно, если бы предположили, что это относится к архитектуре «дели и умножай», показанной выше. Однако это не так. Системы ФАПЧ с дробным N основаны на более сложной технологии, в которой значение делителя частоты изменяется между N и N+1 таким образом, чтобы создать среднее значение делителя, равное N плюс дробь. Этот процесс приводит к нежелательной модуляции частоты ГУН, но отрицательные эффекты этой модуляции могут быть смягчены путем рандомизации и формирования шума.
Заключение
Мы обсудили влияние «коэффициента усиления» на переходной процесс в петле ФАПЧ и увидели, что необходимый коэффициент затухания (демпфирования) можно восстановить, увеличив коэффициент усиления ГУН. Что касается синтеза частот, мы теперь знаем, что делитель частоты (расположенный перед фазовым детектором) может расширить наши возможности умножения частоты. Мы закончили с кратким объяснением архитектуры дробного N. Возможно, мы рассмотрим системы ФАПЧ с дробным N в будущем.
Если вы хотите поэкспериментировать с ФАПЧ самостоятельно, не стесняйтесь сэкономить немного времени, загрузив мою схему для LTspice по ссылке ниже.
