Как оптимизировать переходной процесс петли ФАПЧ
В данной статье мы рассмотрим математические соотношения, которые помогут вам разработать систему ФАПЧ (PLL), которая быстро и плавно захватит/зафиксирует входную частоту.
Вспомогательная информация
Если у вас уже есть опыт работы с системами фазовой автоподстройки частоты (ФАПЧ, PLL) и вы знакомы с ними, но вам нужны некоторые теоретические сведения о проектировании фильтра петли ФАПЧ, эта статья (надеюсь) будет именно тем, что вам нужно. Если вы интересуетесь работой фильтра петли ФАПЧ, но еще не имеете четкого представления об общей работе системы ФАПЧ, я предлагаю вам начать с чтения статей, перечисленных выше.
На следующем рисунке показана базовая структурная схема системы ФАПЧ, а под структурной схемой – схема для моей реализации ФАПЧ в LTspice.
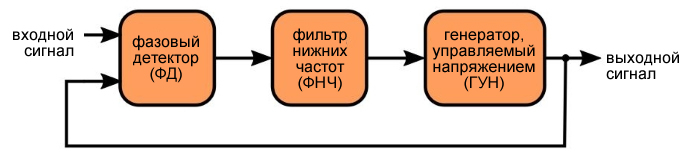
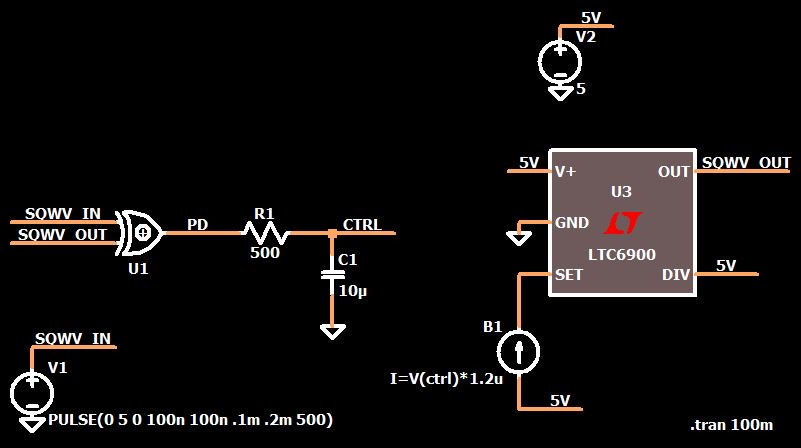
Данная статья о том, как спроектировать фильтр петли ФАПЧ для оптимального переходного процесса, но, как вы увидите, это проектирование не может происходить «изолировано», потому на переходной процесс влияют также коэффициент усиления фазового детектора и коэффициент усиления ГУН.
Сглаживание/фильтрация/усреднение
Если вы читали предыдущие статьи о ФАПЧ (PLL), то уже знаете, почему эта система должна включать в себя фильтр нижних частот: нам нужно что-то, что преобразует выходной сигнал фазового детектора в медленно меняющееся напряжение, которое можно использовать для регулировки частоты генератора, управляемого напряжением. Есть разные способы понять это:
- Фильтр нижних частот ослабляет высокочастотные составляющие в выходном сигнале фазового детектора, поэтому низкочастотное поведение становится доминирующим.
- Выходной сигнал фазового детектора эквивалентен ШИМ сигналу, и фильтр сглаживает его до соответствующего уровня аналогового сигнала.
- Фильтр обеспечивает математическую работу извлечения среднего значения из выходного сигнала фазового детектора.
Это всё правильные толкования, и если одно из них имеет для вас больше смысла, чем другие, непременно сосредоточьтесь на нем. Критически важным шагом в понимании (и запоминании) является формирование образов и связей, которые гармонируют с вашими собственными когнитивными особенностями.
Математика
Строгий математический анализ переходного процесса системы ФАПЧ не прост. Однако мы можем получить адекватные результаты оптимизации, используя довольно простую линейную аппроксимацию. В этой аппроксимации каждому из трех функциональных блоков назначается передаточная функция. Если вы объедините их в одну передаточную функцию, которая описывает всю систему ФАПЧ, то получите выражение второго порядка, которое можно использовать для нахождения формул собственной частоты петли ФАПЧ и ее коэффициента затухания. Это система второго порядка (то есть двухполюсная), потому что фильтр нижних частот вносит один полюс, и ГУН вносит один полюс; таким образом, эта аппроксимация справедлива только для ФНЧ первого порядка.
Я не думаю, что вам нужно слишком беспокоиться о математических подробностях; главное, что мы можем использовать коэффициент затухания для проектирования фильтра нижних частот. Вот формула для коэффициента затухания петли ФАПЧ (обычно он обозначается как ζ, но я буду использовать DR («damping ratio» или «коэффициент затухания/демпфирования», он же «damping factor» или «демпинг фактор»)).
\[DR=\frac{1}{2}\sqrt{\frac{\omega_{ФНЧ}}{K}}\]
Как видите, существует довольно прямая связь между коэффициентом затухания и частотой среза ФНЧ. Однако возникает два вопроса:
- Что такое K?
- Какое значение мы должны использовать для DR?
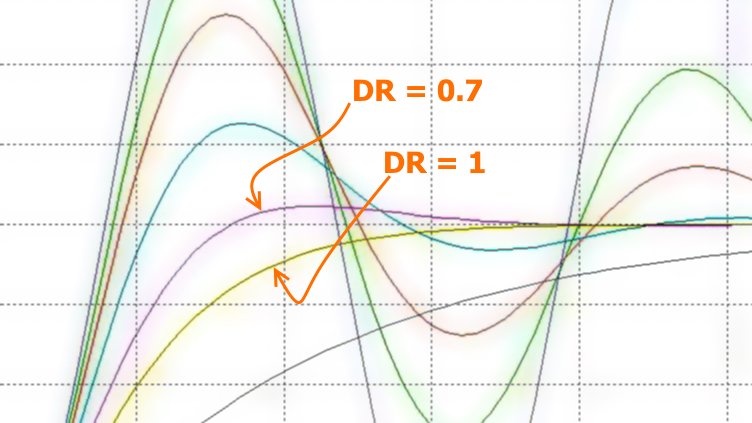
Второй вопрос проще первого. Мы моделируем ФАПЧ как типовую систему управления второго порядка, что означает, что применяются те же принципы затухания: если DR слишком низок, переходная функция будет демонстрировать чрезмерные колебания. Если он слишком высок, системе потребуется много времени для достижения состояния покоя. Как показано на следующем графике, идеальный DR составляет около 0,7 (если вы хотите, чтобы система была немного недодемпфирована), около 1,0 (если вы хотите, чтобы система была немного передемпфирована), или где-то посередине.
Теперь всё, что нам нужно, это K, который представляет общий коэффициент усиления системы; он рассчитывается путем умножения коэффициента усиления фазового детектора на коэффициент усиления ГУН. К сожалению, здесь всё становится сложнее.
Баланс частоты / коэффициента усиления / частоты среза
Допустим, коэффициент усиления фазового детектора у вас составляет 1 В/радиан (что означает, что один радиан разности фаз между двумя входными сигналами приведет к 1 вольту амплитуды выходного сигнала). Предположим также, что увеличение управляющего напряжения на 1 В увеличивает частоту ГУН на 1000 Гц; поскольку 1000 Гц ≈ 6283 рад/с, коэффициент усиления нашего ГУН составляет 6283 (рад/с)/В.
\[K=K_{ФД}\times K_{ГУН}=1\frac{В}{рад}\times6283\frac{рад/с}{В}=6283\ с^{-1}\]
Если нам нужен DR = 1, то у нас будет следующее уравнение:
\[1=\frac{1}{2}\sqrt{\frac{\omega_{ФНЧ}}{6283\ с^{-1}}}\]
После небольших вычислений мы получим ωФНЧ = 25132 рад/с. Возвращаясь к герцам, мы видим, что частота среза фильтра нижних частот должна составлять 4 кГц. Это кажется вполне разумным результатом, но если вы подумаете над этим числом минуту, то, возможно, осознаете проблему. Что произойдет, если мы захотим использовать ФАПЧ с частотами, которые ниже или сопоставимы с частотой среза ФНЧ? Назначение фильтра нижних частот состоит в том, чтобы сгладить форму сигнала фазового детектора, но это произойдет только тогда, когда частота среза фильтра значительно ниже частот, генерируемых фазовым детектором.
Например, если я рассчитаю общий коэффициент усиления моей системы ФАПЧ в схеме для LTspice, а затем спроектирую RC-фильтр, основываясь на на этом коэффициенте усиления и DR = 1, управляющее напряжение у меня будет выглядеть так:
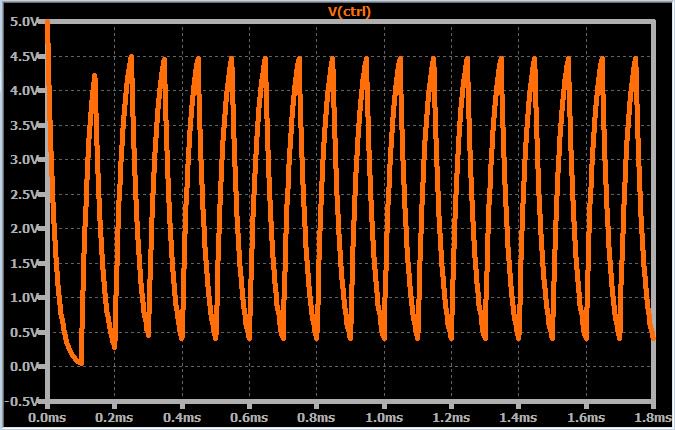
Основная проблема здесь заключается в том, что ωФНЧ нельзя (как я уже говорил в начале статьи) выбирать отдельно. Как видно из формулы DR, показанной выше, для определения DR требуется определенное соотношение между ωФНЧ и K; а ωФНЧ, в свою очередь, ограничена предполагаемым частотным диапазоном системы ФАПЧ. Таким образом, оптимизация переходной характеристики – это не просто вопрос определения K и последующего расчета частоты среза ФНЧ. Скорее, вы должны убедиться, что значение K достаточно мало, чтобы позволить вам выбрать частоту среза, достаточно низкую для ожидаемых условий работы системы ФАПЧ, а затем вы сможете точно настроить частоту среза, используя формулу, которая связывает DR с ωФНЧ и K.
Заключение
В данной статье был представлен небольшой математический анализ системы ФАПЧ (PLL), чтобы объяснить процедуру разработки системы ФАПЧ, которая обеспечивает захват/синхронизацию частоты без чрезмерных колебаний и чрезмерной задержки. Рассчитать соответствующую частоту среза ФНЧ нам позволяет простая формула, основываясь на общем коэффициенте усиления системы ФАПЧ и требуемом коэффициенте затухания/демпфирования. Но коэффициент усиления должен быть достаточно низким, чтобы допустить использование частоты среза, обеспечивающей достаточное затухание высокочастотных составляющих в выходном сигнале фазового детектора.
В следующей статье мы продолжим исследовать эту тему.
