Квадратурные частотная и фазовая демодуляции
В данной статье рассматривается использование квадратурной демодуляции с частотно- и фазо-модулированными сигналами.
Из предыдущей статьи мы знаем, что квадратурная демодуляция создает два низкочастотных сигнала, которые взятые вместе передают информацию, которая была закодирована в сигнал несущей принимаемого сигнала. Более конкретно, эти сигналы I и Q эквивалентны действительной и мнимой частям комплексного числа. Низкочастотный сигнал, содержащийся в модулированном сигнале, соответствует представлению «амплитуда-плюс-фаза» исходных данных, а квадратурная демодуляция преобразует это представление «амплитуда-плюс-фаза» в сигналы I и Q, которые соответствуют декартовому представлению.
Возможно, это неудивительно, что мы можем использовать квадратурную демодуляцию для демодуляции амплитудно-модулированных сигналов, учитывая, что квадратурный демодулятор представляет собой просто два амплитудных демодулятора, приводимых в действие опорными сигналами несущей частоты, которые имеют разность фаз 90°. Однако одной из важнейших характеристик квадратурной демодуляции является ее универсальность. Она работает не только с амплитудной модуляцией, но и с частотной и фазовой модуляциями.
Квадратурная частотная демодуляция
Сначала давайте рассмотрим I и Q сигналы, которые получаются при применении квадратурной демодуляции к сигналу с частотной модуляцией. Принимаемый FM сигнал представляет собой несущую 100 кГц, модулированную синусоидой 100 Гц. Мы используем тот же квадратурный демодулятор, который использовался в моделировании амплитудной модуляции; он имеет два источника напряжения с произвольным поведением для выполнения умножения, а за каждым источником напряжения следует двухполюсный фильтр нижних частот (частота среза составляет ~1 кГц). Для получения информации о том, как в LTspice создать FM сигнал, вы можете обратиться к статье «Как демодулировать частотно-модулированный сигнал».
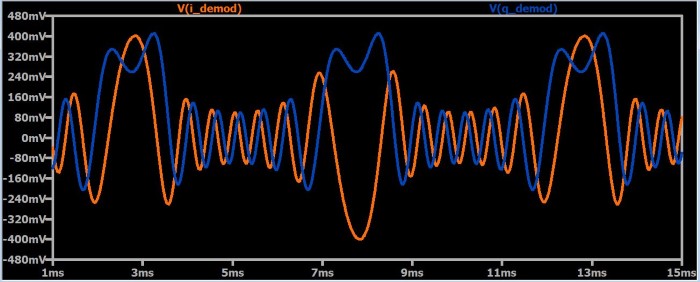
Возможно, распространенной реакцией на эту диаграмму будет замешательство. Как эти странно выглядящие сигналы связаны с синусоидой с постоянной частотой, которая должна получиться в результате процесса демодуляции? Сначала давайте сделаем два замечания:
- Очевидно, что частота сигналов I и Q не является постоянной. Вначале это может показаться немного сбивающим с толку, так как мы знаем, что I/Q модуляция включает в себя амплитудную модуляцию квадратурных несущих. Почему меняется частота? Важно помнить, что эти I/Q сигналы соответствуют модулирующим сигналам, а не квадратурным синусоидам, которые складывались бы вместе в квадратурном модуляторе. Частота модулированных квадратурных несущих не меняется, но низкочастотные сигналы, которые служат модулирующими по амплитуде сигналами, необязательно имеют постоянную частоту.
- Хотя мы не можем интуитивно интерпретировать информацию на этой диаграмме, но мы можем видеть, что сигналы изменяются периодически, и что эти изменения соответствуют периоду (=10 мс) низкочастотного сигнала 100 Гц.
Определение угла
Теперь, когда у нас есть I/Q сигналы, нам нужно как-то их обработать в нормальный демодулированный сигнал. Давайте сначала попробуем подход, который мы использовали с амплитудной модуляцией: используем немного математики для извлечения данных об амплитуде.
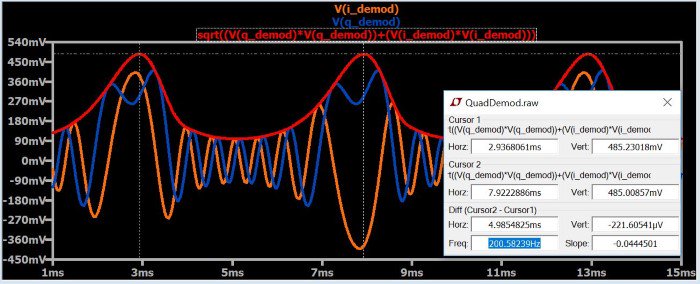
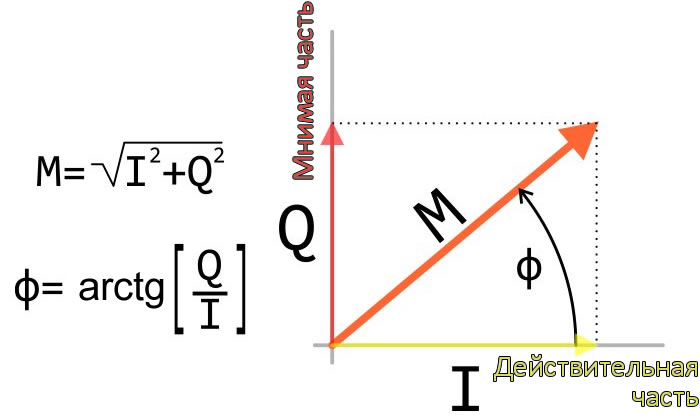
Ясно, что это не сработало: сигнал амплитуды (красный график) не похож на синусоиду, и частота неверна (200 Гц вместо 100 Гц). Однако при дальнейшем рассмотрении становится ясно почему. Исходные данные характеризуются амплитудой и фазой; когда мы применяем формулу \(\sqrt{(I^2+Q^2)}\), мы извлекаем амплитуду. Проблема в том, что исходные данные были закодированы не в амплитуде несущей – они были закодированы в угле (помните, что частотная и фазовая модуляции являются двумя формами угловой модуляции).
Итак, давайте попробуем другую формулу. Давайте извлечем угол из I/Q данных, а не амплитуду. Как показано на рисунке с прямоугольным треугольником выше, мы можем сделать это, применив следующую формулу:
\[ \phi=\text{arctg} \left( \frac{Q}{I} \right) \]
А вот результат:
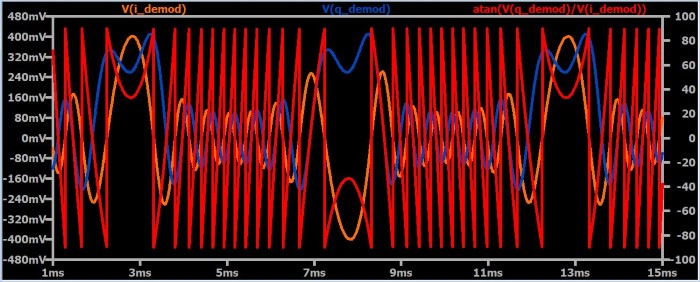
Это выглядит не очень хорошо, но мы реально становимся ближе к цели. Красный график представляет собой мгновенную фазу исходных данных (обратите внимание, что график кажется более неустойчивым, чем есть на самом деле, потому что угол прыгает от –90° до +90°, или наоборот). Частотная модуляция, хотя и основана на фазе, не кодирует информацию непосредственно в фазе несущей. Скорее она кодирует информацию в мгновенной частоте несущей, а мгновенная частота является производной от мгновенной фазы. Итак, что произойдет, если взять производную от красного графика?
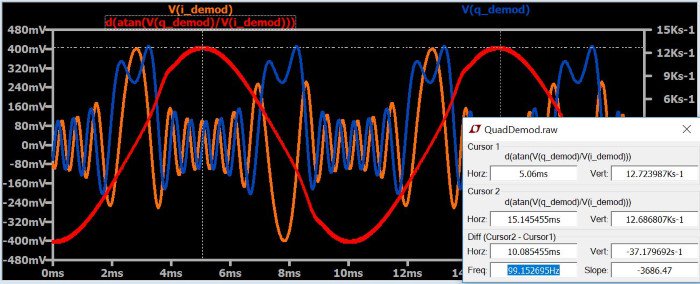
Как вы можете видеть, теперь мы восстановили сигнал, который является синусоидой и имеет ту же частоту, что и исходный низкочастотный сигнал.
Как создать схему арктангенса
На этом этапе вам может стать интересно, почему кто-то беспокоится об I/Q демодуляции. Как кто-то в мире разработал схему, которая генерирует выходной сигнал, соответствующий производной от арктангенса двух входных сигналов? Ну, чтобы ответить на вопрос, заданный в названии этого раздела, вы оцифровываете сигналы и вычисляете арктангенс в прошивке или программном обеспечении. И это подводит нас к важному вопросу: квадратурная демодуляция особенно выгодна в контексте программно-определяемых радиосистем.
Программно-определяемая радиосистема (SDR, software-defined radio) представляет собой систему беспроводной связи, в которой значительная часть функций передатчика и/или приемника реализована с помощью программного обеспечения. Квадратурная демодуляция очень универсальна и позволяет одному приемнику почти мгновенно адаптироваться к различным типам модуляции. Однако, выходные I/Q сигналы гораздо менее просты, чем обычный низкочастотный сигнал, создаваемый стандартными схемами демодуляторов. Вот почему квадратурный демодулятор и цифровой сигнальный процессор формируют такую высокопроизводительную систему: цифровой сигнальный процессор может легко применять сложные математические операции к I/Q данным, создаваемым демодулятором.
Квадратурная фазовая демодуляция
Те же общие соображения, которые мы обсуждали в контексте квадратурной частотной демодуляции, относятся также к квадратурной фазовой демодуляции. Однако для восстановления исходных данных мы берем арктангенс от (Q/I), а не производную от арктангенса от (Q/I), поскольку низкочастотный сигнал кодируется непосредственно в фазе несущей, а не в производной фазы (т.е. частоте).
Следующий график был получен путем применения квадратурной демодуляции к сигналу с фазовой манипуляцией, состоящему из несущей 100 кГц и цифрового низкочастотного сигнала 100 Гц, который вызывает изменения фазы несущей на 180° в зависимости от того, идет ли он с низким или высоким логическим уровнем. Как вы можете видеть, красный график (значение которого соответствует фазе принимаемого сигнала) воспроизводит логические переходы низкочастотного сигнала.
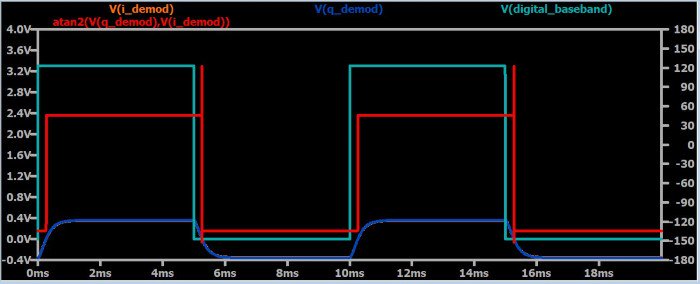
Обратите внимание, что красный график вычисляется с помощью функции "atan2". Стандартный арктангенс ограничен двумя квадрантами (т.е. 180°) декартовой плоскости. Функция atan2 смотрит на отдельные полярности входных значений, чтобы создавать углы, охватывающие все четыре квадранта.
Резюме
- Квадратурная демодуляция может извлекать информацию угла, которая имеет отношение как к частотной модуляции, так и к фазовой модуляции.
- Радиосистемы могут использовать цифровые сигнальные процессоры (в сочетании с аналого-цифровым преобразователем) для применения математического анализа к I/Q сигналам.
- Низкочастотная фаза может быть получена путем вычисления арктангенса отношения Q к I; функция "
atan2" необходима, если система должна иметь возможность воспроизведения полных 360° фазы. - Низкочастотную частоту можно получить, взяв производную от арктангенса отношения Q к I.
