Проводимость
Когда учащиеся впервые видят формулу общего параллельного сопротивления, возникает естественный вопрос: «Откуда эта штука?». Это действительно странная арифметика, и ее происхождение заслуживает хорошего объяснения.
В чем разница между сопротивлением и проводимостью?
Сопротивление, по определению, является мерой «трения», которое компонент представляет для прохождения через него тока. Сопротивление обозначается заглавной буквой «R» и измеряется в единицах «Ом». Однако мы также можем думать об этом электрическом свойстве с обратной ему точки зрения: насколько легко току течь через компонент, а не насколько трудно.
Если сопротивление – это термин, которое мы используем для обозначения меры того, насколько трудно току течь, то хорошим термином, чтобы выразить, насколько легко ток течет, будет проводимость. Математически проводимость – это величина, обратная сопротивлению:
\[проводимость = \frac{1}{сопротивление}\]
Чем больше сопротивление, тем меньше проводимость; и наоборот.
Это должно быть интуитивно понятно, потому что сопротивление и проводимость – противоположные способы обозначения одного и того же важного электрического свойства.
Если сравнивать сопротивления двух компонентов и обнаружится, что компонент «A» имеет сопротивление вдвое меньше сопротивления компонента «B», то в качестве альтернативы мы могли бы выразить это соотношение, сказав, что компонент «A» в два раза более проводящий, чем компонент «B». Если компонент «A» имеет сопротивление, равное только одной трети от сопротивления компонента «B», то мы можем сказать, что он в три раза более проводящий, чем компонент «B», и так далее.
Единица измерения проводимости
В продолжение этой идеи были придуманы символ и единица измерения проводимости. Символ представляет собой заглавную букву «G», а единицей измерения был mho, что означает «ohm» (ом), написанное в обратном порядке (вы думали, что у электронщиков нет чувства юмора?).
Несмотря на свою уместность, единицы измерения mho в последующие годы были заменены единицей Сименс (сокращенно «См», или, в англоязычной литературе, «S»). Это решение об изменении названий единиц измерения напоминает изменение единицы измерения температуры в градусах стоградусной шкалы (degrees centigrade – от латинских слов «centum», т.е. «сто», и «gradus») на градусы Цельсия (degrees Celsius) или изменение единицы измерения частоты c.p.s. (циклов в секунду) в герцы. Если вы ищете здесь какой-то шаблон переименования, то Сименс, Цельсий и Герц – это фамилии известных ученых, имена которых, к сожалению, о природе единиц говорят нам меньше, чем их первоначальные обозначения.
Возвращаясь к нашему примеру с параллельной схемой, мы должны быть в состоянии увидеть, что несколько путей (ветвей) для тока уменьшают общее сопротивление всей цепи, поскольку ток может легче проходить через всю цепь из нескольких ветвей, чем через любую из них отдельно. Что касается сопротивления, дополнительные ветви приводят к меньшему общему значению (ток встречает меньшее сопротивление). Однако с точки зрения проводимости дополнительные ветви приводят к большему общему значению (ток протекает с большей проводимостью).
Общее сопротивление параллельной цепи
Общее сопротивление параллельной цепи меньше, чем любое из сопротивлений отдельных ветвей, потому что параллельные резисторы вместе «сопротивляются» меньше, чем по отдельности:
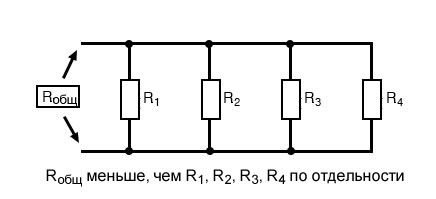
Общая проводимость параллельной цепи
Общая проводимость параллельной цепи больше, чем проводимость любой из отдельных ветвей, потому что параллельные резисторы «проводят» вместе лучше, чем по отдельности:
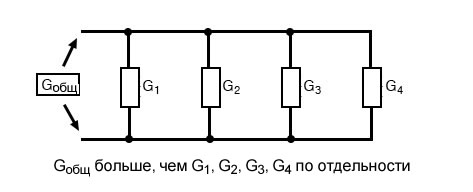
Чтобы быть более точным, полная проводимость в параллельной цепи равна сумме отдельных проводимостей:
\[G_{общ} = G_1 + G_2 + G_3 + G_4\]
Если мы знаем, что проводимость – это не что иное, как математическая величина, обратная (1/x) сопротивлению, мы можем перевести каждый член приведенной выше формулы в сопротивление, подставив величину, обратную каждой соответствующей проводимости:
\[\frac{1}{R_{общ}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + \frac{1}{R_{4}}\]
Решая приведенное выше уравнение для полного сопротивления (вместо значения, обратного общему сопротивлению), мы получим следующую формулу:
\[R_{общ} = \frac{1}{\frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + \frac{1}{R_{4}}}\]
Итак, мы, наконец, пришли к нашей загадочной формуле сопротивления! Проводимость (G) редко используется в качестве практического параметра, поэтому при анализе параллельных цепей часто используется приведенная выше формула.
Резюме
- Проводимость – параметр, противоположный сопротивлению: это мера того, насколько легко электрический ток проходит через что-то.
- Проводимость обозначается буквой «G» и измеряется в сименсах (сокр. См).
- Математически проводимость равна величине, обратной сопротивлению: G = 1/R.
