Простые последовательные схемы

В данной статье мы изложим три принципа, которые необходимо понимать в отношении последовательных цепей:

1. ток: величина тока в последовательной цепи одинакова для любого компонента в цепи;
2. сопротивление: общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений;
3. напряжение: напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.

Давайте взглянем на несколько примеров последовательных цепей, демонстрирующих эти принципы.

Начнем с последовательной схемы, состоящей из трех резисторов и одной батареи:

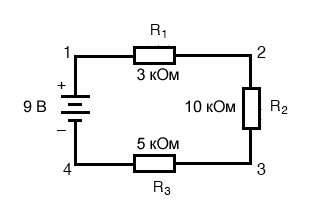
Первый принцип, который следует понимать в отношении последовательных цепей, заключается в следующем:

Величина тока в последовательной цепи одинакова для любого компонента в цепи.

Это потому, что в последовательной цепи есть только один путь для прохождения тока. Поскольку электрический заряд проходит через проводники, как шарики в трубке, скорость потока (скорость шариков) в любой точке цепи (трубки) в любой конкретный момент времени должна быть одинаковой.

Использование закона Ома в последовательных цепях

По расположению 9-вольтовой батареи мы можем сказать, что ток в этой цепи будет течь по часовой стрелке от точки 1 к точке 2, к 3, к 4 и обратно к 1. Однако у нас есть один источник напряжения и три сопротивления. Как мы можем использовать здесь закон Ома?

Важная оговорка к закону Ома заключается в том, что все величины (напряжение, ток, сопротивление и мощность) должны относиться друг к другу с точки зрения одних и тех же двух точек в цепи. Мы можем увидеть эту концепцию в действии на примере схемы с одним резистором ниже.

Использование закона Ома в простой схеме с одним резистором

В схеме с одной батареей и одним резистором мы можем легко вычислить любой параметр, потому что все они применяются к одним и тем же двум точкам в цепи:

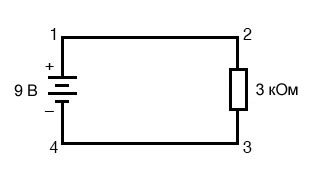
\[I = \frac{E}{R}\]

\[I = \frac{9 \ вольт}{3 \ кОм} = 3 \ мА\]

Поскольку точки 1 и 2 соединены вместе проводом с незначительным сопротивлением, как и точки 3 и 4, мы можем сказать, что точка 1 электрически является общей с точкой 2, а точка 3 электрически общей с точкой 4. Поскольку мы знаем, что мы иметь электродвижущую силу 9 вольт между точками 1 и 4 (непосредственно на батарее), и поскольку точка 2 является общей для точки 1, а точка 3 – общей для точки 4, мы также должны иметь 9 вольт между точками 2 и 3 (непосредственно на резисторе).

Следовательно, мы можем применить закон Ома (I = E/R) к току через резистор, потому что мы знаем напряжение (E) на резисторе и сопротивление (R) этого резистора. Все параметры (E, I, R) относятся к одним и тем же двум точкам в цепи, к одному и тому же резистору, поэтому мы можем безоговорочно использовать формулу закона Ома.

Использование закона Ома в схемах с несколькими резисторами

В схемах, содержащих более одного резистора, мы должны проявлять осторожность в применении закона Ома. В приведенной ниже схеме с тремя резисторами мы знаем, что у нас есть 9 вольт между точками 1 и 4, что является величиной электродвижущей силы, управляющей током через последовательную комбинацию резисторов R₁, R₂ и R₃. Однако чтобы попытаться найти значение тока, мы не можем взять значение 9 вольт и разделить его на 3 кОм, 10 кОм или 5 кОм, потому что мы не знаем, какое напряжение присутствует на любом из этих резисторов по отдельности.

Значение 9 вольт – это общая величина для всей цепи, тогда как значения 3 кОм, 10 кОм и 5 кОм – это отдельные величины для отдельных резисторов. Если бы мы включили значение для общего напряжения в уравнение закона Ома со значением для отдельного сопротивления, результат точно не будет соответствовать какому-либо параметру в реальной цепи.

Для R₁ закон Ома будет связывать величину напряжения на R₁ с током через R₁ при заданном сопротивлении R₁, 3 кОм:

\[I_{R1} = \frac{E_{R1}}{3 \ кОм} \qquad E_{R1} = I_{R1} \times (3 \ кОм)\]

Но, поскольку нам неизвестно напряжение на R₁ (только общее напряжение, подаваемое батареей на комбинацию из трех последовательных резисторов), и мы не знаем ток через R₁, мы не можем производить никаких вычислений ни по одной из этих формул. То же самое касается R₂ и R₃: мы можем применять уравнения закона Ома тогда и только тогда, когда все члены представляют свои соответствующие величины между одними и теми же двумя точками в цепи.

Так что мы можем сделать? Нам известно напряжение источника (9 вольт), приложенное к последовательной комбинации резисторов R₁, R₂ и R₃, и мы знаем сопротивление каждого резистора, но поскольку эти величины не находятся в одном контексте, мы не можем использовать закон Ома для определения тока в цепи. Если бы мы только знали, каково общее сопротивление цепи: тогда мы могли бы вычислить общий ток, используя наше значение для общего напряжения (I=E/R).

Объединение нескольких резисторов в эквивалентный общий резистор

Это подводит нас ко второму принципу последовательных цепей:

Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.

Это должно быть интуитивно понятно: чем больше последовательно соединенных резисторов, через которые должен протекать ток, тем труднее току будет протекать.

В примере у нас были последовательно соединены резисторы 3 кОм, 10 кОм и 5 кОм, что дало нам общее сопротивление 18 кОм:

\[R_{общ} = R_1 + R_2 + R_3\]

\[R_{общ} = 3 \ кОм + 10 \ кОм + 5 \ кОм\]

\[R_{общ} = 18 \ кОм\]

По сути, мы вычислили эквивалентное сопротивление R₁, R₂ и R₃ вместе взятых. Зная его, мы могли бы перерисовать схему с одним эквивалентным резистором, представляющим последовательную комбинацию R₁, R₂ и R₃:

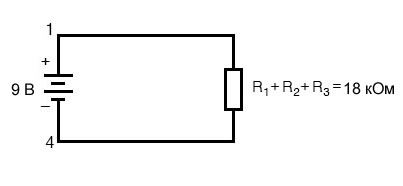
Расчет тока цепи с использованием закона Ома

Теперь у нас есть вся необходимая информация для расчета тока цепи, потому что у нас есть напряжение между точками 1 и 4 (9 вольт) и сопротивление между точками 1 и 4 (18 кОм):

\[I_{общ} = \frac{E_{общ}}{R_{общ}}\]

\[I_{общ} = \frac{9 \ В}{18 \ кОм} = 500 \ мкА\]

Расчет напряжений на компонентах по закону Ома

Зная, что ток одинаков во всех компонентах последовательной цепи (и мы только что определили ток через батарею), мы можем вернуться к нашей исходной принципиальной схеме и отметить ток через каждый компонент:

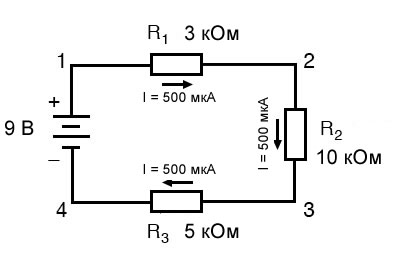
Теперь, когда мы знаем величину тока, протекающего через каждый резистор, мы можем использовать закон Ома, чтобы определить падение напряжения на каждом из них (применяя закон Ома в его надлежащем контексте):

\[E_{R1} = I_{R1}R_1 \qquad E_{R2} = I_{R2}R_2 \qquad E_{R3} = I_{R3}R_3\]

\[E_{R1} =(500 \ мкА)(3 \ кОм) = 1,5 \ В\]

\[E_{R2} =(500 \ мкА)(10 \ кОм) = 5 \ В\]

\[E_{R3} =(500 \ мкА)(5 \ кОм) = 2,5 \ В\]

Обратите внимание на падения напряжения на каждом резисторе, и как сумма этих падений напряжения (1,5 + 5 + 2,5) равна напряжению батареи (источника питания): 9 вольт.

Это третий принцип последовательной схемы:

Напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.

Анализ простых последовательных схем с помощью «табличного метода» и закона Ома

Метод, который мы только что использовали для анализа этой простой последовательной схемы, можно упростить для лучшего понимания. Используя таблицу для перечисления всех напряжений, токов и сопротивлений в цепи, становится очень легко увидеть, какие из этих величин могут быть правильно связаны в любом уравнении закона Ома:

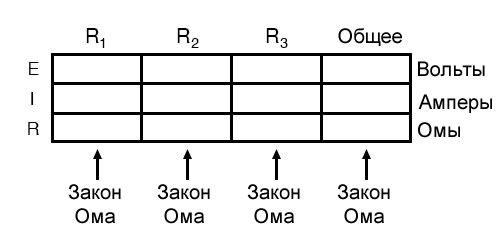
Правило с такой таблицей – применять закон Ома только к значениям в конкретном вертикальном столбце. Например, E_R1 только с I_R1 и R₁; E_R2 только с I_R2 и R₂; и т.д. Анализ начинается с заполнения тех элементов таблицы, которые даны нам с самого начала:

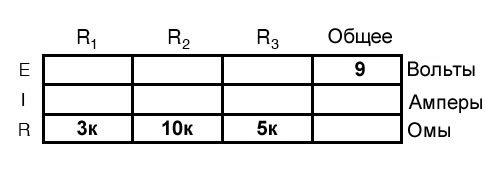
Как вы можете видеть из расположения данных, мы не можем применить 9 вольт E_общ (общее напряжение) к любому из сопротивлений (R₁, R₂ или R₃) в любой формуле закона Ома, потому что они находятся в разных столбцах. Напряжение батареи 9 В не подается напрямую на R₁, R₂ или R₃. Однако мы можем использовать наши «правила» последовательных цепей, чтобы заполнить пустые места в горизонтальной строке. В этом случае мы можем использовать правило последовательных сопротивлений для определения общего сопротивления из суммы отдельных сопротивлений:

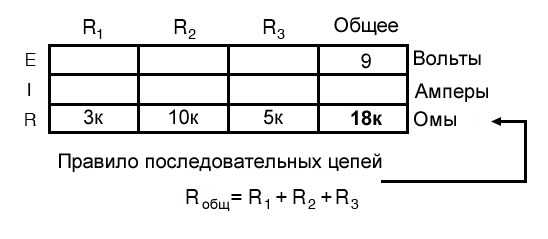
Теперь, введя значение общего сопротивления в крайний правый столбец («Общее»), мы можем применить закон Ома I=E/R к общему напряжению и общему сопротивлению, чтобы получить общий ток 500 мкА:

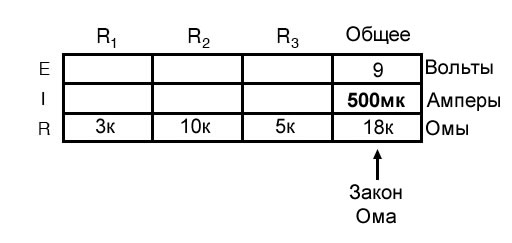
Затем, зная, что ток одинаков во всех компонентах последовательной цепи (еще одно «правило» последовательной схемы), мы можем заполнить токи для каждого резистора из только что рассчитанного значения тока:

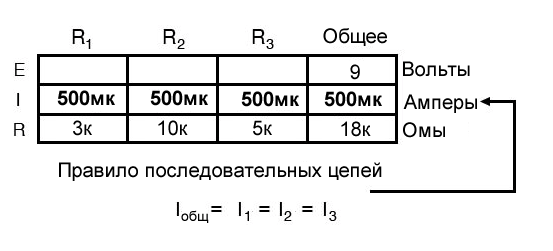
Наконец, мы можем использовать закон Ома, чтобы определить падение напряжения на каждом резисторе, по столбцу за раз:

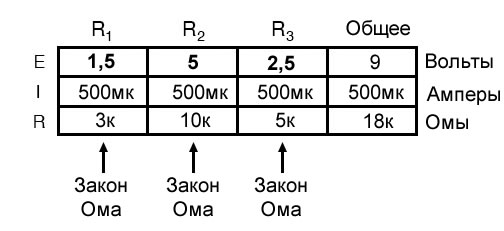
Проверка расчетов с помощью компьютерного анализа (SPICE)

Ради интереса, для автоматического анализа этой схемы мы можем использовать компьютер. Это будет хороший способ проверить наши расчеты, а также познакомиться с компьютерным анализом. Во-первых, мы должны описать схему в формате, распознаваемом программным обеспечением.

Программа SPICE, которую мы будем использовать, требует, чтобы все электрически уникальные точки в цепи были пронумерованы, а размещение компонентов понималось по тому, какие из этих пронумерованных точек или «узлов» они разделяют. Для ясности я пронумеровал четыре угла схемы в нашем примере с 1 по 4. Однако SPICE требует, чтобы в схеме где-то был нулевой узел, поэтому я перерисую схему, немного изменив схему нумерации:

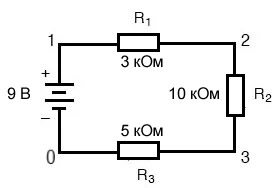
Все, что я здесь сделал, – это изменил номер нижнего левого угла схемы на 0 вместо 4. Теперь я могу ввести несколько строк текста в файл, описывающий схему в терминах, понятных SPICE, в комплекте с парой дополнительные строки кода, предписывающих программе отображать данные о напряжении и токе. Этот файл в терминологии SPICE известен как список соединений (netlist):

series circuit
v1 1 0
r1 1 2 3k
r2 2 3 10k
r3 3 0 5k
.dc v1 9 9 1
.print dc v(1,2) v(2,3) v(3,0)
.end

Теперь всё, что мне нужно сделать, это запустить программу SPICE для обработки списка соединений и вывода результатов:

Эта распечатка говорит нам, что напряжение батареи составляет 9 вольт, а падение напряжения на R₁, R₂ и R₃ составляет 1,5, 5 и 2,5 вольт соответственно. Падения напряжения на любом компоненте в SPICE обозначаются номерами узлов, между которыми находится компонент, поэтому v(1,2) относится к напряжению между узлами 1 и 2 в цепи, которые являются точками, между которыми расположен R₁.

Порядок номеров узлов важен: когда SPICE выводит число для v(1,2), он учитывает полярность так же, как если бы мы держали вольтметр с красным измерительным проводом на узле 1 и черным измерительным проводом на узле. 2. У нас также есть значение, показывающее силу тока (хотя и со знаком минус) на уровне 0,5 мА или 500 мкА. Это значение отображается как отрицательное число в анализе SPICE из-за необычного способа обработки вычислений токов в SPICE. Итак, наш математический анализ был подтвержден компьютером.

Таким образом, последовательная цепь определяется как имеющая только один путь, по которому может течь ток. Из этого определения следуют три правила последовательных цепей: через все компоненты протекает одинаковый ток; общее сопротивление может быть получено путем сложения отдельных сопротивлений; а падения напряжения в сумме дают большее общее напряжение. Все эти правила выводятся из определения последовательной цепи. Если вы полностью понимаете это определение, то правила – не более чем сноски к определению.

Резюме

• Компоненты в последовательной цепи имеют одинаковый ток: I_общ = I₁ = I₂ =. . . = I_n
• Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений: R_общ = R₁ + R₂ +. . . + R_n
• Общее напряжение в последовательной цепи равно сумме отдельных падений напряжения E_общ = E₁ + E₂ +. . . + E_n

Теги