Простые параллельные схемы
В данной статье мы изложим три принципа, которые вы должны понимать в отношении параллельных цепей:
- напряжение: напряжение одинаково на всех компонентах в параллельной цепи;
- ток: общий ток цепи равен сумме токов отдельных ветвей;
- сопротивление: отдельные сопротивления уменьшают общее сопротивление, а не увеличивают его.
Давайте взглянем на несколько примеров параллельных схем, демонстрирующих эти принципы.
Начнем с параллельной схемы, состоящей из трех резисторов и одной батареи:
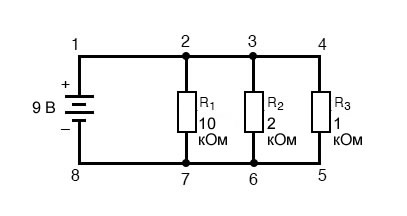
Напряжение в параллельных цепях
Первый принцип, который следует понимать в отношении параллельных цепей, заключается в том, что напряжение на всех компонентах в цепи одинаково. Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между этими наборами общих точек, всегда должно быть одинаковым.
Следовательно, в приведенной выше схеме напряжение на R1 равно напряжению на R2, которое равно напряжению на R3, которое равно напряжению на батарее.
Это равенство напряжений можно представить в таблице для наших начальных значений:
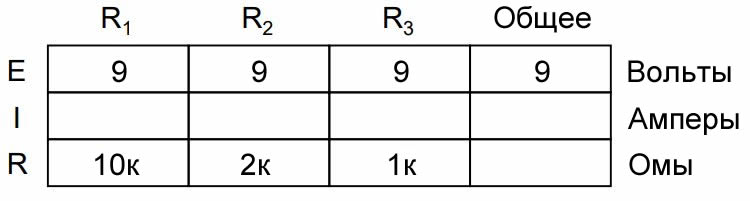
Применение закона Ома к простым параллельным цепям
Как и в случае с последовательными цепями, применимо то же предостережение для закона Ома: чтобы вычисления работали правильно, значения напряжения, тока и сопротивления должны быть в одном контексте.
Однако в приведенной выше схеме мы можем немедленно применить закон Ома к каждому резистору, чтобы найти его ток, потому что нам известно напряжение на каждом резисторе (9 вольт) и сопротивление каждого резистора:
\[I_{R1}=\frac{E_{R1}}{R_1} \qquad I_{R2}=\frac{E_{R2}}{R_2} \qquad I_{R3}=\frac{E_{R3}}{R_3}\]
\[I_{R1}=\frac{9 \ В}{10 \ кОм} = 0,9 \ мА\]
\[I_{R2}=\frac{9 \ В}{2 \ кОм} = 4,5 \ мА\]
\[I_{R3}=\frac{9 \ В}{1 \ кОм} = 9 \ мА\]
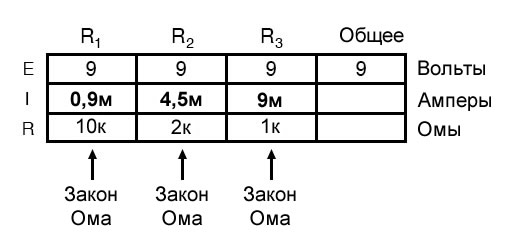
На данный момент мы еще не знаем, каков общий ток или полное сопротивление для этой параллельной цепи, поэтому мы не можем применить закон Ома к крайнему правому столбцу («Общее»). Однако если мы внимательно подумаем о том, что происходит, то должно стать очевидным, что полный ток должен равняться сумме всех отдельных токов резисторов («ветвей»):
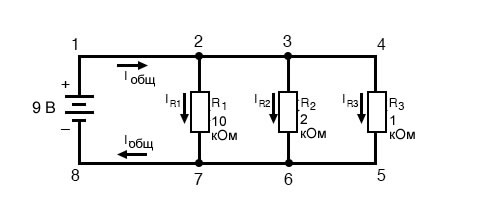
По мере того, как полный ток выходит из положительной (+) клеммы батареи в точке 1 и проходит по цепи, часть тока отделяется в точке 2 и проходит через R1, еще часть отделяется в точке 3, чтобы пройти через R2, а оставшаяся часть проходит через R3. Подобно реке, разветвляющейся на несколько меньших потоков, общая скорость всех потоков должна быть равна скорости потока всей реки.
То же самое происходит, когда токи через R1, R2 и R3 объединяются, чтобы течь обратно к отрицательному выводу батареи (-) в направлении точки 8: поток тока из точки 7 в точку 8 должен равняться сумме токов (ветвей) через R1, R2 и R3.
Это второй принцип параллельных цепей: полный ток цепи равен сумме токов отдельных ветвей.
Используя этот принцип, мы можем заполнить ячейку для общего тока в нашей таблице суммой IR1, IR2 и IR3:
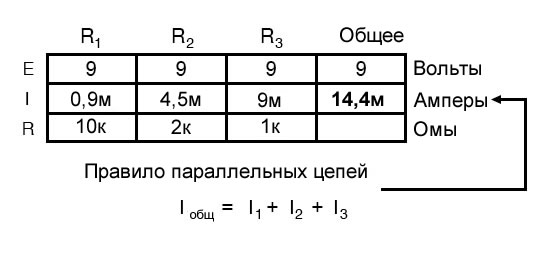
Как рассчитывать полное сопротивление в параллельных цепях
Наконец, применив закон Ома к крайнему правому столбцу («Общее»), мы можем вычислить полное сопротивление цепи:
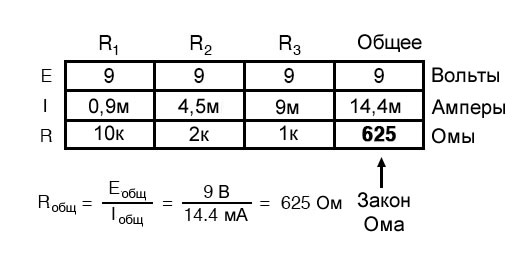
Формула сопротивления в параллельных цепях
Обратите внимание на кое-что очень важное. Общее сопротивление цепи составляет всего 625 Ом: меньше, чем у любого из отдельных резисторов. В последовательной цепи, где полное сопротивление было суммой отдельных сопротивлений, общее сопротивление должно было быть больше, чем сопротивление любого из резисторов по отдельности.
Однако здесь, в параллельной цепи, верно обратное: мы говорим, что отдельные сопротивления уменьшают общее сопротивление, а не увеличивают его.
Этот принцип завершает нашу триаду «правил» для параллельных цепей, для которых, как и для последовательных цепей, есть три правила: для напряжения, тока и сопротивления.
Математически зависимость между общим сопротивлением и отдельными сопротивлениями в параллельной цепи выглядит следующим образом:
\[R_{общ} = \frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}}\]
Эта же базовая форма уравнения работает для любого количества резисторов, соединенных вместе параллельно, просто добавьте столько членов 1/R к знаменателю дроби, сколько необходимо для размещения всех параллельных резисторов в цепи.
Как изменить схему нумерации параллельной цепи для SPICE
Как и в случае с последовательной схемой, мы можем использовать компьютерный анализ, чтобы перепроверить наши расчеты. Во-первых, конечно, мы должны описать нашу схему для SPICE в понятных ему терминах. Я начну с повторного рисования схемы:

И снова мы обнаруживаем, что исходная схема нумерации, используемая для идентификации точек в цепи, должна быть изменена для работы со SPICE.
В SPICE все электрически общие точки должны иметь одинаковые номера узлов. Так SPICE узнает, что с чем и как связано.
В простой параллельной схеме все точки являются электрически общими в одном из двух наборов точек. Для нашей схемы провод, соединяющий верхние части всех компонентов, будет иметь один номер узла, а провод, соединяющий нижние части компонентов, будет иметь другой номер.
Оставаясь верным соглашению о включении нуля в качестве номера узла, я выбираю числа 0 и 1:
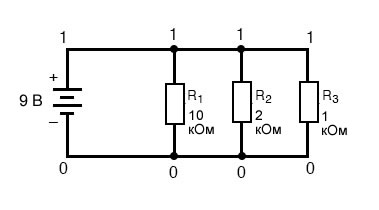
Пример, подобный этому, делает обоснование выбора номеров узлов в SPICE довольно понятным. Поскольку все компоненты имеют общие наборы чисел, компьютер «знает», что все они подключены параллельно друг другу.
Чтобы отобразить в SPICE токи ветвей, нам нужно последовательно с каждым резистором вставить источник нулевого напряжения, а затем связать наши измерения тока с этими источниками.
По какой-то причине создатели программы SPICE сделали так, чтобы ток можно было рассчитывать только через источник напряжения. Это несколько раздражающее требование программы моделирования SPICE. После добавления каждого из этих «фиктивных» источников напряжения необходимо создать несколько новых номеров узлов, чтобы подключить их к соответствующим резисторам:
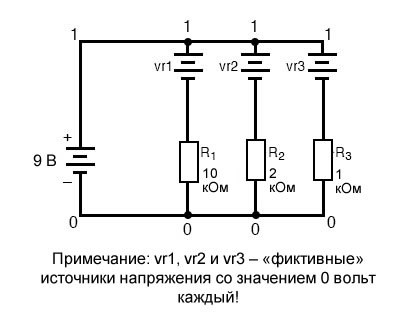
Все фиктивные источники напряжения настроены на 0 вольт, чтобы не влиять на работу схемы.
Как проверить результаты компьютерного анализа
Файл описания схемы, или список соединений, выглядит так:
Parallel circuit
v1 1 0
r1 2 0 10k
r2 3 0 2k
r3 4 0 1k
vr1 1 2 dc 0
vr2 1 3 dc 0
vr3 1 4 dc 0
.dc v1 9 9 1
.print dc v(2,0) v(3,0) v(4,0)
.print dc i(vr1) i(vr2) i(vr3)
.end
Запустив компьютерный анализ, мы получаем следующие результаты:
| v1 | v(2) | v(3) | v(4) |
|---|---|---|---|
| 9.000E+00 | 9.000E+00 | 9.000E+00 | 9.000E+00 |
| напряжение батареи | напряжение R1 | напряжение R2 | напряжение R3 |
| v1 | i(vr1) | i(vr2) | i(vr3) |
|---|---|---|---|
| 9.000E+00 | 9.000E-04 | 4.500E-03 | 9.000E-03 |
| напряжение батареи | ток R1 | ток R2 | ток R3 |
Эти значения действительно совпадают со значениями, рассчитанными ранее по закону Ома: 0,9 мА для IR1, 4,5 мА для IR2 и 9 мА для IR3. При параллельном подключении, естественно, все резисторы имеют одинаковое падение напряжения (9 вольт, как на батарее).
Три правила параллельных цепей
Таким образом, параллельная цепь определяется как такая цепь, в которой все компоненты подключены между одними и теми же наборами электрически общих точек. Другими словами, все компоненты соединены клеммами друг с другом. Из этого определения следуют три правила параллельных цепей:
- все компоненты имеют одинаковое напряжение;
- сопротивления уменьшают меньшее общее сопротивление;
- токи ветвей в сумме равны большему общему току.
Как и в случае с последовательными цепями, все эти правила находят корень в определении параллельной цепи. Если вы полностью понимаете это определение, то правила – не более чем сноски к определению.
Резюме
- Компоненты в параллельной цепи имеют одинаковое напряжение: Eобщ = E1 = E2 = . . . = En
- Общее сопротивление в параллельной цепи меньше любого из отдельных сопротивлений: Rобщ = 1 / (1/R1 + 1/R2 + . . . + 1/Rn)
- Общий ток в параллельной цепи равен сумме токов отдельных ветвей: Iобщ = I1 + I2 + . . . +In.
