Как преобразование Лапласа используется в проектировании схем?
В данной статье мы кратко рассмотрим, как преобразование Лапласа может помочь нам разрабатывать схемы, работающие с затухающими и устойчивыми синусоидальными сигналами.
В ответе на этот частый инженерный вопрос (FEQ, Frequent Engineering Question) мы кратко рассмотрим анализ и проектирование цепей переменного тока с использованием преобразования Лапласа.
Распространенной задачей в электротехнике является проектирование и анализ цепей, в которых токи и напряжения непрерывно изменяются синусоидальным образом.
Когда мы работаем с этим типом цепей, мы обычно фокусируемся на амплитуде и фазе сигналов, а не на непрерывных изменениях. Мы предполагаем, что сигналы являются и всегда будут синусоидами, поскольку такие компоненты, как резисторы, конденсаторы и идеализированные усилители, не приводят к потере синусоидальной формы сигнала.
Однако эти компоненты влияют на амплитуду и фазу сигналов.
Анализ цепей с помощью векторов
Распространенным методом анализа цепей относительно амплитуды и фазы является использование векторов, представляющих собой комплексные числа, представляющие синусоидальные электрические сигналы.
Когда мы выполняем векторный анализ, мы работаем в частотной области, и выражения для тока или напряжения записываются как функции от jω, где j – мнимая единица, а ω – угловая частота. Вектора помогают нам работать со схемами, в которых используются устойчивые синусоидальные сигналы.
Затухающие и устойчивые синусоиды
Преобразование Лапласа расширяет этот подход, включая не только устойчивые, но и затухающие синусоиды. Оно преобразует функцию времени f(t) в функцию комплексной частоты. Для обозначения комплексной частоты мы используем букву s, и, таким образом, после применения преобразования Лапласа f(t) становится F(s). Комплексная частота определяется следующим образом:
\[s = \sigma + j\omega\]
где σ – это постоянная, которая влияет на то, как изменяется амплитуда синусоиды. При σ = 0 затухания нет.
Инженеры-электрики обычно работают с устойчивыми, а не с затухающими синусоидами. Это позволяет нам предполагать, что s = jω, и мы можем произвести преобразование Лапласа сигнала, просто взяв выражение F(jω) и заменив jω на s.
Преобразование Лапласа в анализе цепей переменного тока
Преобразование Лапласа широко используется при проектировании и анализе цепей и систем переменного тока. Мы можем выразить токи, напряжения и импедансы как функции от s. Например, импеданс конденсатора можно записать как
\[Z_C(s)=\frac{1}{sC}\]
Отношения между входом и выходом мы так же часто записываем как функции от s. Например, передаточная функция фильтра нижних частот может быть выражена следующим образом:
\[T(s)=\frac{a_0}{s+\omega _0}\]
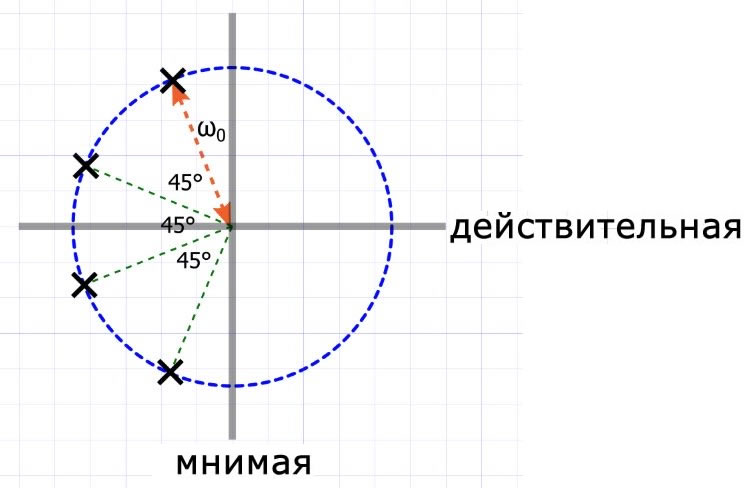
Мы также выполняем графический анализ передаточной функции, нанося ее полюсы и нули на то, что называется s-плоскостью. Следующая диаграмма представляет собой представление на s-плоскости передаточной функции фильтра Баттерворта четвертого порядка.
Материалы для дальнейшего чтения
В данной статье мы рассмотрели, как преобразование Лапласа может помочь нам расширить наш анализ цепей переменного тока с помощью векторов для включения в анализ затухающих и устойчивых синусоид. Чтобы освежить в памяти некоторые другие основы, такие как передаточные функции и сдвиг фазы в аналоговых схемах, ознакомьтесь со статьями из списка ниже.
- Понятие полюсов и нулей в передаточных функциях
- Понятие передаточных функций фильтров нижних частот
- Понятие сдвига фазы в аналоговых цепях
