Полюсы и нули фильтра Баттерворта
В данной статье рассматривается фильтр нижних частот Баттерворта, также известный как фильтр с максимально плоской характеристикой, с точки зрения его диаграммы нулей и полюсов.
Многие люди слышали термин «фильтр Баттерворта» и использовали фильтры такого типа в своих схемах. Вам, конечно, не обязательно быть экспертом в теории фильтров, чтобы успешно включать схемы фильтров в свои проекты. Однако в некоторых случаях полезно понимать некоторые вещи более подробно. Во времена SPICE, гугления и калькуляторов фильтров нам иногда нужно сделать шаг назад и подумать о теоретической и концептуальной основе, на которой строится рабочая схема.
Моя цель в данной статье – дать представление о фильтре Баттерворта, представив и обсудив аспекты его диаграммы полюсов и нулей.
Полюсы и нули
Ранее я написал статью о полюсах и нулях в теории фильтров, посмотрите ее на случай, если вам понадобится более обширная информация по этой теме. Полюсы представляют частоты, которые приводят к тому, что знаменатель передаточной функции равен нулю, и они вызывают уменьшение наклона амплитудно-частотной характеристики системы. Нули представляют частоты, которые приводят к тому, что числитель передаточной функции равен нулю, и они вызывают увеличение наклона амплитудно-частотной характеристики системы.
В данной статье мы сосредоточимся на фильтре нижних частот Баттерворта, который имеет, как минимум, два полюса и не имеет нулей. (Все фильтры нижних частот имеют, по крайней, мере один ноль при ω = бесконечность, но он не появляется на диаграмме полюсов и нулей и обычно может игнорироваться.)
Диаграмма полюсов и нулей
Информация о полюсах и нулях системы может передаваться визуально с помощью отметки их расположения в комплексной плоскости. Если вы читали мои статьи о диаграмме Найквиста или о комплексно-сопряженных полюсах, или статью доктора Серхио Франко о расщеплении полюсов, вы знакомы с концепцией диаграммы полюсов и нулей.
Следующий рисунок демонстрирует ее структуру.
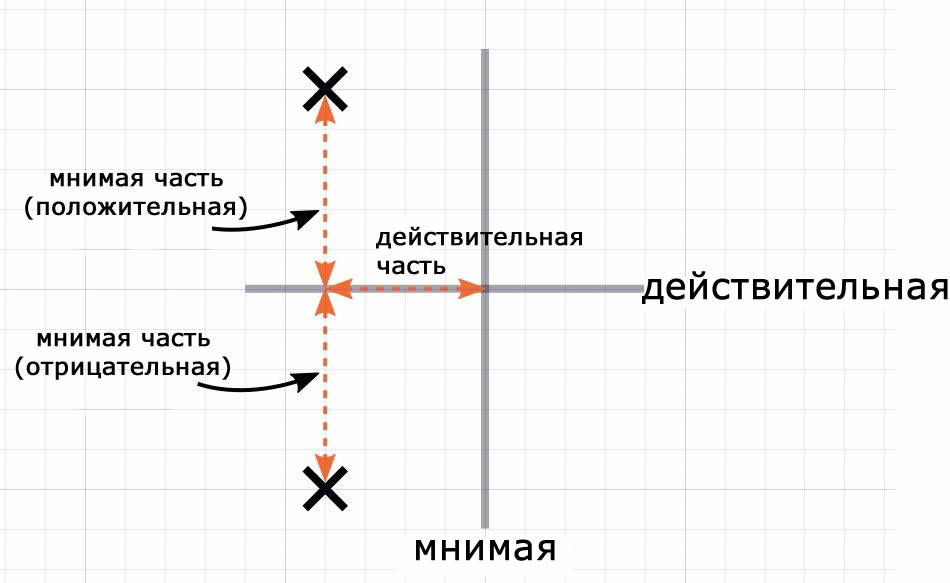
Расположение полюса или нуля определяется его действительной частью, которая откладывается по горизонтали, и его мнимой частью, которая откладывается по вертикали. Полюсы обозначаются крестиком (✕), а нули – кружком (◯). В приведенном выше примере два полюса представляют собой комплексно-сопряженную пару, поскольку их действительные части равны, а мнимые части равны по величине, но противоположны по знаку.
Диаграмма полюсов и нулей – это удобное и эффективное средство передачи важной информации о системе фильтра. Как вы можете видеть на диаграмме ниже, она показывает как частоту полюсов/нулей, так и добротность (Q):

Фильтр Баттерворта
Я использую здесь слово «фильтр», чтобы подчеркнуть тот факт, что «фильтр» Баттерворта на самом деле является классом цепей, имеющих одинаковые основные характеристики.
Как и в случае с большинством других вещей в жизни, у вас не может быть одной системы, устройства или материала, которые лучше всех остальных. Вместо этого у нас есть компромиссы: производительность против стоимости, прочность против веса, свободное время против баланса на банковском счете, и так далее.
Приоритетом фильтра Баттерворта является гладкость АЧХ в полосе пропускания, и именно это объединяет различные варианты фильтров Баттерворта: они сводят к минимуму величину изменений на амплитудно-частотной характеристике, которые происходят до частоты среза. Это контрастирует с фильтром Чебышева, который для повышения крутизны перехода от полосы пропускания к полосе задерживания допускает «пульсации» АЧХ в полосе пропускания.
Гладкость в полосе пропускания можно увидеть на следующем графике, который представляет собой амплитудно-частотную характеристику фильтра Баттерворта четвертого порядка.
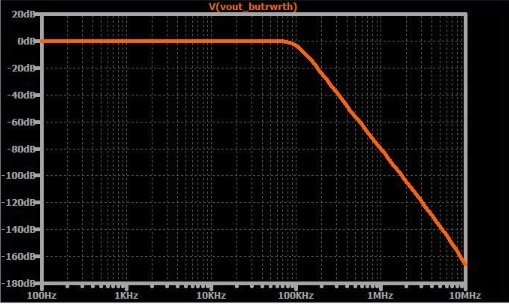
Диаграмма полюсов и нулей фильтра Баттерворта
Чтобы получить фильтр Баттерворта, пропускающий нижние частоты, нам нужно создать передаточную функцию, полюсы которой расположены следующим образом:
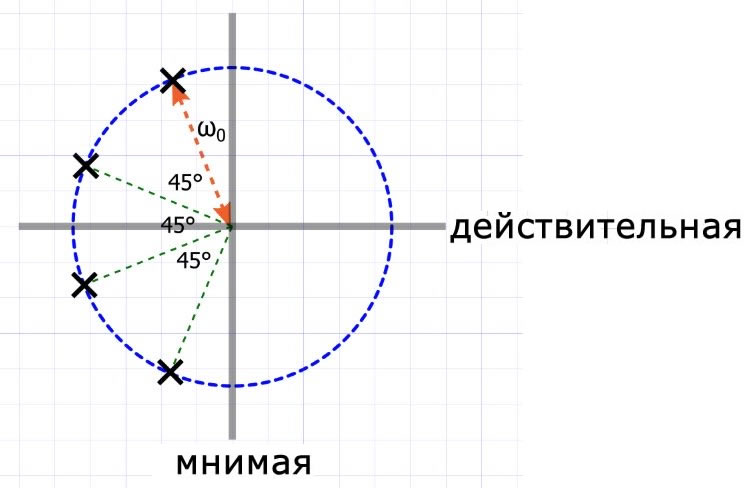
Извлечь информацию из этой диаграммы вам помогут следующие ключевые моменты:
- Основная характеристика диаграммы полюсов и нулей фильтра нижних частот Баттерворта – это то, что угловое расстояние между полюсами одинаковое, и они лежат вдоль полукруглой траектории в левой полуплоскости.
- Все точки на окружности имеют одинаковое расстояние от центра окружности. Таким образом, расстояние между началом координат и каждым полюсом одинаково, а это, в свою очередь, означает, что все полюсы имеют одинаковую частоту.
- Угол, разделяющий полюсы, равен 180°/N, где N – порядок фильтра. В приведенном выше примере N = 4, а угол между полюсами равен 180°/4=45°.
- Равное угловое расстояние между полюсами фильтра Баттерворта указывает на то, что фильтры четного порядка будут иметь только комплексно-сопряженные полюса. Фильтры нечетного порядка будут иметь комплексно-сопряженные полюсы плюс один чисто вещественный полюс, который расположен на отрицательной части действительной оси на расстоянии ω0 от начала координат.
- Все полюса имеют одинаковые ω0, но горизонтальное расстояние от начала координат у них разное. Таким образом, полюсы имеют разные значения добротности.
Заключение
Диаграмма полюсов и нулей, которую мы рассмотрели в данной статье, – это не просто способ описания фильтра нижних частот. Скорее, конфигурация полюсов является теоретической основой для создания фильтра Баттерворта. Учитывая требуемую частоту среза и порядок фильтра, мы бы выбрали компоненты так, чтобы расположение полюсов соответствовало схеме Баттерворта.
Переход от диаграммы полюсов и нулей к значениям номиналов компонентов не особенно прост; еще до появления удобных программных инструментов использовались предварительно рассчитанные таблицы, и я предполагаю, что вам никогда не придется выполнять этот процесс вручную. Тем не менее, хорошо хотя бы что-то знать о базовых концепциях, и я надеюсь, что вам был интересен этот теоретический обзор ФНЧ Баттерворта.
