Понятие полюсов и нулей в передаточных функциях

Данная статья объясняет, что такое полюсы и нули, и обсуждает, как полюсы и нули передаточной функции связаны с поведением схем аналоговых фильтров относительно амплитуды и фазы.

В предыдущей статье я представил два стандартных способа представления передаточной функции в s-области для RC фильтра нижних частот первого порядка. Давайте кратко рассмотрим некоторые важные концепции.

• Передаточная функция математически выражает поведение фильтра в частотной области при передаче сигнала от входа к выходу.
• Мы можем написать передаточную функцию относительно переменной s, которая представляет собой комплексную частоту, и мы можем заменить s на jω, когда нам нужно вычислить амплитуду и сдвиг фазы на конкретной частоте.
• Нормированная форма передаточной функции похожа на шаблон, который помогает нам быстро определять определяющие характеристики фильтра.
• Математическое манипулирование нормированной передаточной функцией первого порядка позволяет нам продемонстрировать, что частота среза фильтра – это частота, на которой амплитуда уменьшается на 3 дБ, а фаза сдвигается на –45°.

Полюсы и нули

Предположим, что у нас есть передаточная функция, в которой переменная s появляется как в числителе, так и в знаменателе. В этой ситуации, по крайней мере, одно значение s приведет к тому, что числитель будет равен нулю, и, по крайней мере, одно значение s приведет к тому, что знаменатель будет равен нулю. Значение, при котором числитель равен нулю, является нулем передаточной функции, а значение, которое приводит к нулю в знаменателе, является полюсом передаточной функции.

Давайте рассмотрим следующий пример:

\[T(s)=\frac{Ks}{s+\omega _{0}}\]

В этой системе мы имеем ноль при s = 0 и полюс при s = –ω₀.

Полюсы и нули являются определяющими характеристиками фильтра. Если вы знаете расположение полюсов и нулей, то у вас много информации о том, как система будет реагировать на сигналы с разными входными частотами.

Влияние полюсов и нулей

Диаграмма Боде (логарифмическая амплитудно-частотная характеристика, АЧХ) обеспечивает простую визуализацию взаимосвязи между полюсом или нулем и поведением системы при передаче сигнала от входа к выходу.

Частота полюса соответствует угловой частоте, при которой наклон кривой АЧХ уменьшается на 20 дБ/декада, а ноль соответствует угловой частоте, при которой наклон увеличивается на 20 дБ/декада. В следующем примере амплитудно-частотная характеристика представляет собой аппроксимацию амплитудного отклика системы, которая имеет полюс при 10² радиана в секунду (рад/с) и ноль при 10⁴ рад/с.

Влияние на фазу

В предыдущей статье мы видели, что математическим источником фазо-частотной характеристики фильтра нижних частот является функция арктангенса. Если мы используем функцию арктангенса (точнее, функцию отрицательного арктангенса), чтобы сгенерировать график зависимости фазы (в градусах) от частоты в логарифмическом масштабе, мы получим следующий график:

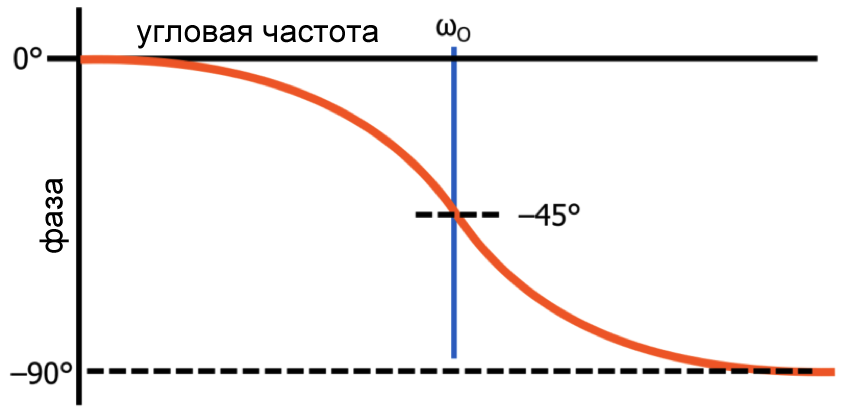
Аппроксимация логарифмической фазо-частотной характеристики для сдвига фазы, генерируемого полюсом, представляет собой прямую линию, представляющую сдвиг фазы -90°. Эта линия центрируется на частоте полюса и имеет наклон –45 градусов на декаду, что означает, что наклонная линия начинается за одну декаду до частоты полюса и заканчивается через одну декаду после частоты полюса. Влияние нуля будет таким же, за исключением того, что линия имеет положительный наклон, поэтому итоговый сдвиг фазы составляет +90°.

В следующем примере представлена система, которая имеет полюс при 10² рад/с и ноль при 10⁵ рад/с.

Скрытый ноль

Если вы читали предыдущую статью, вы знаете, что передаточная функция фильтра нижних частот может быть записана следующим образом:

\[T(s)=\frac{a_0}{s+\omega_0}\]

У этой системы есть ноль? Если мы применим определение, данное ранее в этой статье, мы сделаем вывод, что его нет – переменная s не появляется в числителе, и поэтому никакое значение s не приведет к тому, что числитель станет равным нулю.

Однако оказывается, что у нее на самом деле есть ноль, и чтобы понять почему, нам нужно рассмотреть более обобщенное определение полюсов и нулей передаточной функции: ноль (z от «zero») возникает при значении s, которое заставляет передаточную функцию уменьшаться до нуля, а полюс (p от «pole») возникает при значении s, которое заставляет передаточную функцию стремиться к бесконечности:

\[\lim_{s\rightarrow z}T(s)=0\]

\[\lim_{s\rightarrow p}T(s)=∞\]

Имеет ли фильтр нижних частот первого порядка значение s, которое приводит к T(s) → 0? Да, это так, а именно, s = ∞. Таким образом, система фильтра нижних частот первого порядка имеет полюс в точке ω₀ и ноль в точке ω = ∞.

Я попытаюсь дать физическую интерпретацию нуля при ω = ∞: это указывает на то, что фильтр не может «всегда» продолжать увеличивать ослабление (где «всегда» относится к частоте, а не ко времени). Если вам удастся создать входной сигнал, частота которого продолжает увеличиваться до тех пор, пока она не «достигнет» бесконечности рад/с, то ноль при s = ∞ заставит фильтр прекратить увеличивать ослабление, т.е. наклон амплитудно-частотной характеристики увеличится с –20 дБ/декада до 0 дБ/декада.

Заключение

Мы изучили основные теоретические и практические аспекты полюсов и нулей передаточной функции и увидели, что можем создать прямую связь между частотами полюса и нуля фильтра и его амплитудно-частотной и фазо-частотной характеристиками. В следующей статье мы рассмотрим передаточную функцию фильтра верхних частот первого порядка.

Теги