Понятие передаточных функций фильтров нижних частот
Данная статья дает некоторое представление о взаимосвязи между передаточной функцией в s-области и поведением фильтра нижних частот первого порядка.
В последнее время я довольно много пишу на тему фильтров, и хотя я сосредоточился на практических соображениях, я чувствую необходимость объяснить некоторые важные теоретические концепции в пользу тех, кто хотел бы более подробно понять и проанализировать поведение аналоговых фильтров. В настоящее время каждый имеет доступ к программным инструментам, которые делают сложное проектирование фильтров относительно безболезненным, но я не думаю, что было бы разумно полностью игнорировать математические основы просто потому, что они не являются строго необходимыми для выполнения многих реальных задач проектирования.
s-область
Отклик фильтра может быть выражен передаточной функцией в s-области; переменная s появляется из преобразования Лапласа и представляет комплексную частоту. Например:
\[T(s) = \frac{K}{1+ \left( \frac{s}{\omega_0} \right) }\]
Эта передаточная функция является математическим описанием поведения фильтра нижних частот первого порядка в частотной области. Выражение в s-области эффективно передает общие характеристики, и если мы хотим вычислить конкретную информацию об амплитуде и фазе, всё, что нам нужно сделать, это заменить s на jω, а затем вычислить выражение при заданной угловой частоте.
Вам может быть интересно, откуда берутся K и ω0 – вы, вероятно, никогда не видели принципиальной схемы, в которой значения компонентов были выражены в значениях K и ω0. Идея в том, что K и ω0 подобны частям шаблона, и в следующем разделе мы рассмотрим взаимосвязь между этим шаблоном и принципиальной схемой.
Анализ схем в s-области
RC фильтр нижних частот является частотно-зависимым делителем напряжения. При анализе в s-области импеданс резистора равен R, а импеданс конденсатора равен \(\frac{1}{sC}\).
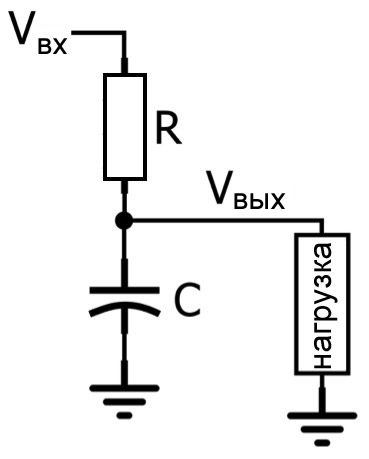
\[\frac{V_{вых}}{V_{вх}} = {\frac{1}{sC} \over \frac{1}{sC} + R} = \frac{1}{1+sRC}\]
Если мы сравним это выражение с нормированной передаточной функцией, то увидим, что K = 1 и \(\omega_0 = \frac{1}{RC}\). Удобство использования нормированной формы становится понятным, как только вы узнаете, что представляют собой K и ω0: K – это коэффициент усиления схемы при постоянном напряжении, а ω0 – это частота среза. Таким образом, сравнивая передаточную функцию схемы с нормированной передаточной функцией, вы можете сразу же сформулировать выражения для двух определяющих характеристик фильтра нижних частот первого порядка, а именно для коэффициента усиления при постоянном напряжении и частоты среза.
Другой нормированной формой передаточной функции фильтра нижних частот первого порядка является следующее:
\[T(s)=\frac{a_0}{s+\omega_0}\]
Мы можем встроить передаточную функцию схемы в этот шаблон, если разделим числитель и знаменатель на RC:
\[T(s)= \frac{1}{1+sRC} \rightarrow { \frac{1}{RC} \over s + \frac{1}{RC} } \]
Таким образом, \(a_0=\frac{1}{RC}\), и \(\omega_0 = \frac{1}{RC}\). Эта форма напрямую не дает нам коэффициент усиления по постоянному напряжению, но если мы вычислим нормированное выражение для s = 0, то получим
\[T(s=0) = \frac{a_0}{\omega_0}\]
Это означает, что коэффициент усиления по постоянному напряжению нашего RC-фильтра равен
\[\left( \frac{1}{RC} \right) / \left( \frac{1}{RC} \right) = 1\]
А коэффициент усиления по постоянному напряжению, равный единице, – это именно то, что мы ожидаем от пассивного фильтра нижних частот.
Понятие частоты среза
Мы видели, что ω0 в стандартной передаточной функции представляет частоту среза, но каково математическое основание этого факта?
Во-первых, давайте, преобразуем стандартную передаточную функцию в s-области в эквивалентную передаточную функцию jω.
\[T(s) = \frac{K}{1 + \frac{s}{\omega_0}} \rightarrow T(j\omega) = \frac{K}{1 + j\frac{\omega}{\omega_0}}\]
Теперь давайте вычислим выражение при частоте среза.
\[T(j\omega = j\omega_0) = \frac{K}{1 + j\frac{\omega_0}{\omega_0}}= \frac{K}{1+j}\]
Знаменатель является комплексным числом, поэтому модуль будет равен
\[|T(j\omega = j\omega_0)|= \frac{K}{\sqrt{1^2+1^2}} = \frac{K}{\sqrt{2}}\]
Поскольку K – это коэффициент усиления по постоянному напряжению, очень низкочастотный входной сигнал с амплитудой в один вольт приведет к выходному сигналу с амплитудой в K вольт. Если входная частота увеличивается до ω0 радиан в секунду, выходная амплитуда будет равна \(\frac{K}{\sqrt{2}}\). Коэффициент \(\frac{1}{\sqrt{2}}\) соответствует –3 дБ, и, как вы, вероятно, знаете, другое название частоты среза – это частота –3 дБ.
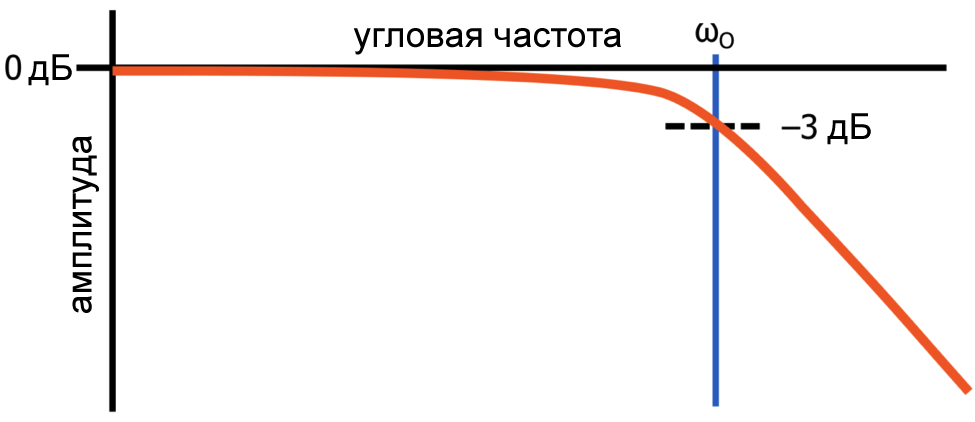
Этот простой анализ передаточной функции ясно продемонстрировал, что частота среза – это просто частота, на которой амплитудно-частотная характеристика фильтра снижается на 3 дБ относительно выходного уровня на очень низкой частоте.
Частота среза и сдвиг фазы
Частота среза фильтра нижних частот имеет особое значение также в отношении фазо-частотной характеристики схемы. Если мы напишем комплексное число в форме x + jy, мы рассчитаем фазу следующим образом:
\[\theta=\text{arctg}\left( \frac{y}{x} \right)\]
Таким образом, общая фазо-частотная характеристика нашего RC фильтра низких частот следующей:
\[\theta(\omega)= -\text{arctg}\left( \frac{\frac{\omega}{\omega_0}}{1} \right)= -\text{arctg}\left( \frac{\omega}{\omega_0} \right)\]
Если мы вычислим это выражение при ω = ω0, сдвиг фазы будет равен
\[-\text{arctg}\left( \frac{\omega_0}{\omega_0} \right) = -\text{arctg}\left( 1 \right) = -45^\circ\]

Максимальный сдвиг фазы, создаваемый фильтром нижних частот первого порядка, составляет 90°, поэтому этот анализ говорит нам, что частота среза является «центром» фазо-частотной характеристики схемы – другими словами, это частота, на которой фильтр создает половину своего максимального сдвига фазы.
Заключение
Я надеюсь, что вам понравилось это краткое введение в концепции s-области и анализ передаточных функций. Поначалу математические основы схем аналоговых фильтров могут быть немного пугающими, но я думаю, что стоит потратить некоторое время на то, чтобы получить некоторое представление об этих темах. Я продолжу исследовать эту тему в будущих статьях.
