Анализ диаграммы Найквиста в LTspice
В данной статье объясняется, как создать и настроить диаграмму Найквиста в LTspice и как добавить этот график в частотный анализ.
В предыдущих четырех статьях мы рассмотрели довольно много информации, касающейся характеристик и применений графиков Найквиста.
Познакомьтесь со статьями серии по ссылкам ниже.
Вспомогательная информация
- Как использовать диаграмму Найквиста (амплитудно-фазовую частотную характеристику) для частотного анализа
- Частота среза на диаграмме Найквиста
- Диаграммы Найквиста для фильтров второго порядка
- Как использовать диаграмму Найквиста для анализа устойчивости
Принципиальное отличие диаграммы Найквиста от логарифмических амплитудно-частотной и фазо-частотной характеристик (графиков Боде) состоит в том, что график Найквиста использует полярную систему координат, и, следовательно, график Найквиста может одновременно передавать информацию и об амплитуде, и об угле. Таким образом, график Найквиста предоставляет ясную информацию о взаимосвязи между амплитудно-частотной и фазо-частотной характеристиками схемы. Из этого следует, что этот график эффективно выражает значение амплитуды при частоте среза, поскольку местоположение частоты среза на комплексной плоскости можно будет легко определить.
Мы видели, что метод визуализации Найквиста – это простой способ получить общее представление о добротности фильтра второго порядка, и он особенно полезен, когда мы хотим быстро оценить устойчивость усилителя. Основное ограничение графика Найквиста, а именно отсутствие конкретных числовых значений частот, во многих применениях делает его плохой заменой логарифмическим амплитудно-частотной и фазо-частотной характеристикам (графикам Боде). Однако, как вы увидите позже в данной статье, это ограничение не распространяется на графики Найквиста, сгенерированные LTspice.
Диаграмма Найквиста в LTspice
На самом деле, график Найквиста очень легко создается в LTspice. Когда вы запускаете моделирование для частотного анализа и затем щелкаете по узлу, LTspice по умолчанию выдает вам графики логарифмических АЧХ и ФЧХ. Если вы щелкните правой кнопкой мыши по вертикальной оси, вы увидите окно с блоком «Representation» (представление). Используйте выпадающее меню, чтобы выбрать «Nyquist».
После нажатия «ОК» вы, вероятно, увидите что-то, что не очень похоже на диаграмму Найквиста.
Например:
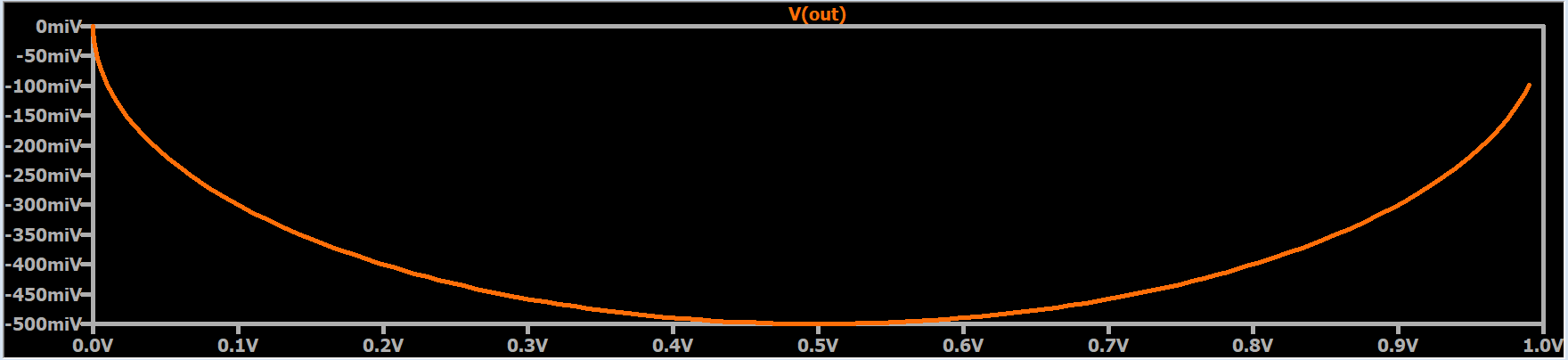
Почему мой график Найквиста выглядит неправильно?
Для этого есть две причины:
- во-первых, визуальный формат окна графика не соответствует комплексной плоскости, которая обычно представлена в виде графической области, в которой две оси имеют одинаковые отношения между числовыми значениями и линейным пространством;
- во-вторых, оси расположены вдоль левого и нижнего краев графика, как на графике в декартовой системе координат; на полярном графике мы ожидаем, что оси будут нарисованы так, чтобы они проходили через точку (0, 0).
Чтобы устранить первую проблему, измените пределы оси таким образом, чтобы обе оси имели одинаковый числовой диапазон, а затем измените размер окна графика так, чтобы оно стало квадратным. Если я хочу убедиться, что кривая является математически точным представлением передаточной функции, я помещаю добрую старую линейку рядом с экраном и корректирую окно графика, пока отображаемая длина горизонтальной оси не станет равной отображаемой длине вертикальной оси.
Для второй проблемы всё, что вам нужно сделать, это активировать курсор и перемещать его по кривой, пока он не достигнет точки (0, 0). Теперь у вас есть горизонтальные и вертикальные линии, которые делят ваш график Найквиста на четыре квадранта. Я рекомендую принудительно (если необходимо) включить обе оси для включения положительных и отрицательных значений, чтобы вы могли четко видеть все четыре квадранта.
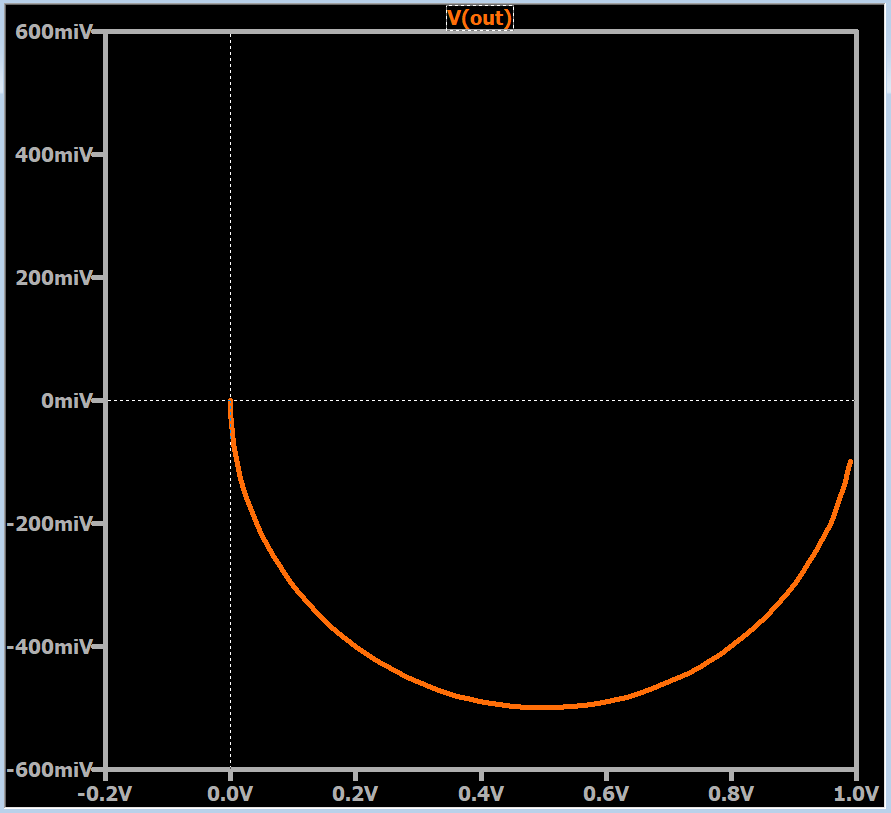
Амплитуда и фаза
Как видно из примера, обе оси имеют единицы измерения вольты, но метки на вертикальной оси включают букву «i», чтобы напомнить нам, что это мнимое измерение комплексной плоскости. Если вы активируете второй курсор, вы можете перемещать его вдоль кривой, и LTspice сообщит вам амплитуду (т.е. \(\sqrt{(Re)^2+(Im)^2}\)) и фазу сигнала.
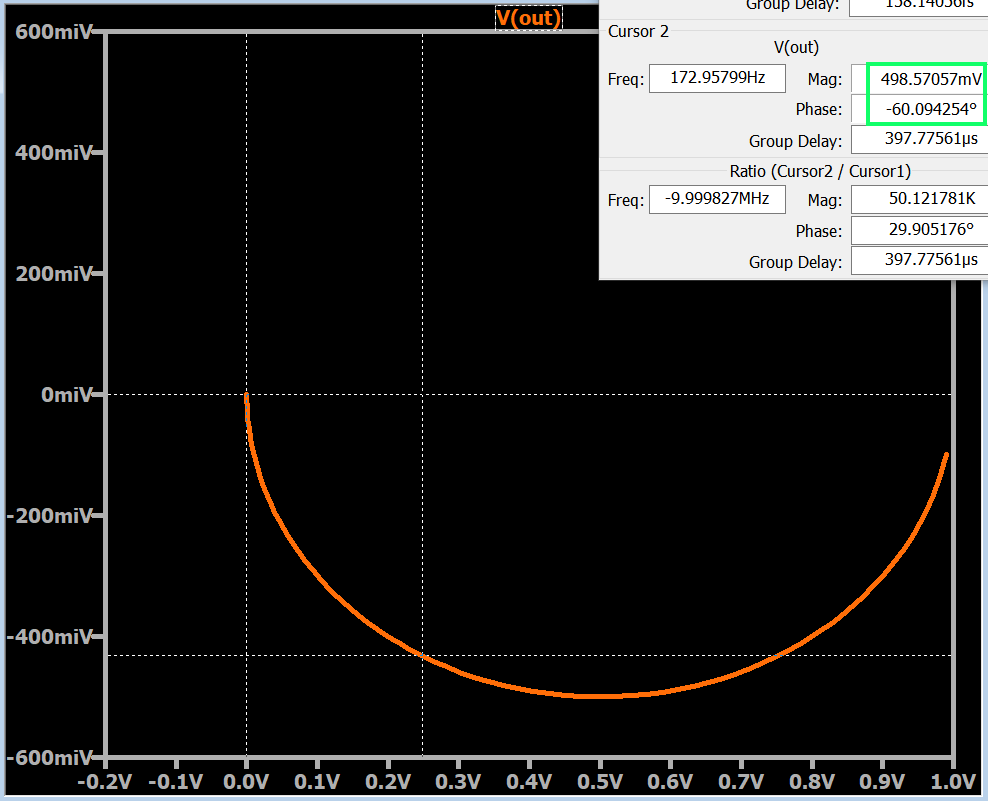
Частота на графике Найквиста в LTspice
Типовой график Найквиста не может предоставить числовую информацию о частоте, потому что он представляет бесконечный диапазон значений частоты. Всё, что делится на бесконечность, равно нулю, поэтому, если бы мы попытались проанализировать график Найквиста с точки зрения обычной пропорциональности, любое конечное числовое значение частоты (10 Гц, 1 кГц, 100 МГц и т. д.) было бы расположено в начальной точке кривой.
Однако диаграмме Найквиста в LTspice удается объединить кривую, форма которой соответствует бесконечному частотному диапазону, с числовыми значениями частот, которые можно ожидать от графиков АЧХ и ФЧХ. Это значительно повышает привлекательность методики Найквиста, потому что вы можете использовать курсоры, чтобы найти усиление и сдвиг фазы на заданной частоте или частоту, на которой схема имеет заданное усиление или сдвиг фазы.
Пример графика Найквиста в LTspice
Примеры графиков, показанные в этой статье, представляют передаточную функцию RC фильтра нижних частот первого порядка. Значения компонентов R = 160 Ом и C = 10 мкФ, что приводит к частоте среза приблизительно 100 Гц.
Те из вас, кто читал предыдущие статьи (особенно вторую статью серии о частотах среза на графиках Найквиста), знают, что точка на кривой, соответствующая частоте среза, имеет угол -45°, и именно ее мы видим на графике Найквиста в LTspice, показанном ниже.
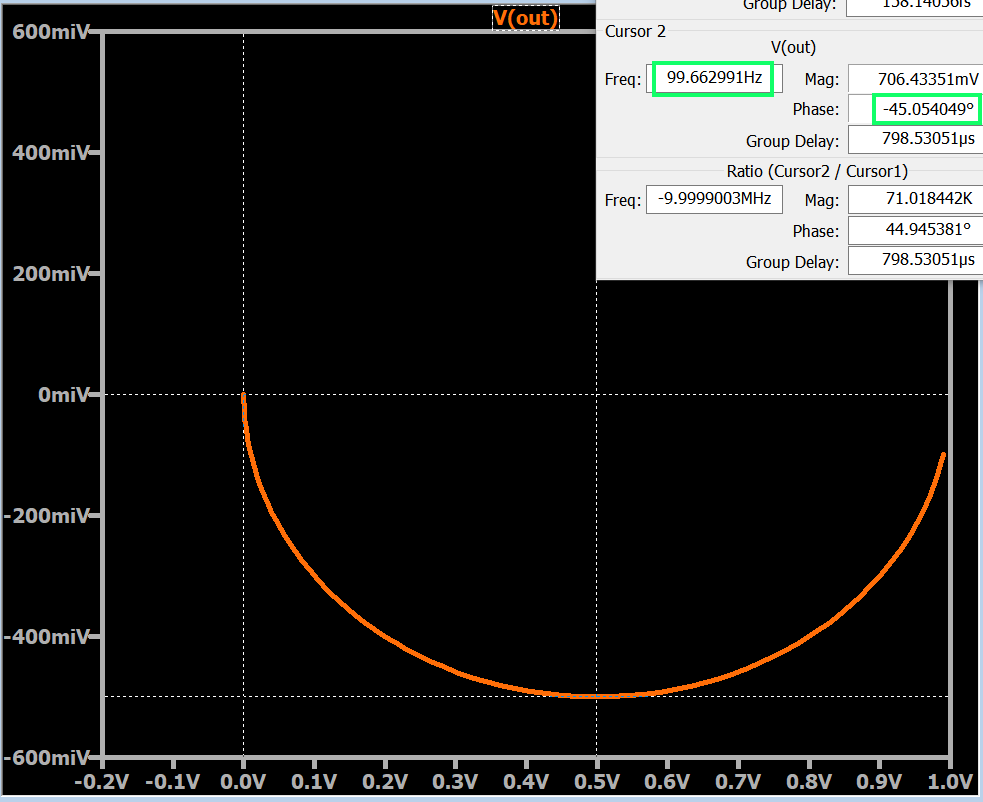
Последнее замечание: как вы могли заметить, диаграмма не содержит стрелки, указывающие направление увеличения частоты. Стрелка не нужна, потому что эта информация доступна с помощью курсоров.
Заключение
Надеюсь, что эта статья дала вам хорошее представление функциональности диаграммы Найквиста в LTspice. Если у вас есть какие-либо соответствующие советы или рекомендации, не стесняйтесь поделиться ими в разделе комментариев ниже.
В следующей статье мы будем использовать график Найквиста в LTspice для анализа устойчивости.
