Частота среза на диаграмме Найквиста
Данная статья продолжает наше исследование диаграммы Найквиста, рассматривая взаимосвязь между кривой графика и частотой среза фильтра.
В предыдущей статье мы видели, что частотная характеристика системы может быть представлена графиком в полярной системе координат, на котором кривая показывает амплитуду и фазу при изменении частоты от нуля до бесконечности. Мы называем его графиком Найквиста (или диаграммой Найквиста), и это интересная альтернатива гораздо более распространенному графику Боде (логарифмическим амплитудно-частотной и фазо-частотной характеристикам).
Следующая диаграмма была представлена в конце предыдущей статьи и дает хороший визуальный обзор основной информации, которую мы можем извлечь из графика Найквиста для фильтра первого порядка.
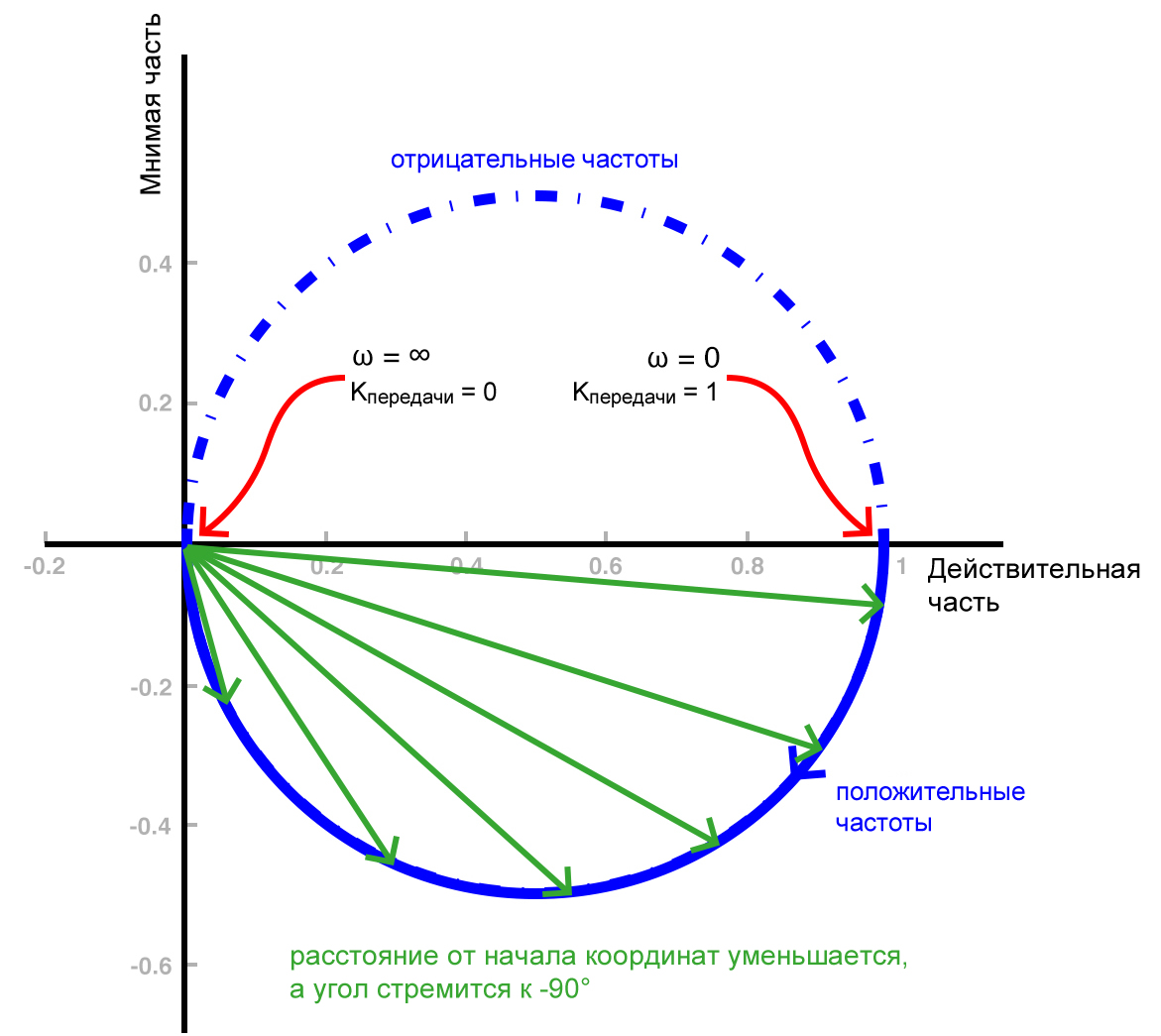
Важность частоты среза
Приведенная выше диаграмма не включает в себя одну очень важную деталь, а именно, частоту среза фильтра. Передаточная функция в s-области для фильтра нижних частот первого порядка может быть выражена следующим образом:
\[T(s)=\frac{K}{1+\left(\frac{s}{\omega _{0}}\right)}\]
Эта формула говорит нам, что единственными отличительными характеристиками данного фильтра нижних частот являются K и ω0. Параметр K – это коэффициент усиления фильтра при постоянном напряжении. Пассивные компоненты не способны усиливать сигнал, поэтому, если мы имеем дело только с RC фильтрами нижних частот первого порядка, мы можем игнорировать K, потому что он всегда будет равен 1. Оставшийся параметр ω0 – это частота среза. Таким образом, мы можем полностью описать RC фильтр нижних частот, просто указав частоту среза.
Определение частоты среза
Кривая на диаграмме Найквиста, конечно, не имеет типового спада характеристики, который мы хорошо знаем из графиков амплитудно-частотных характеристик, и фактически график Найквиста не дает нам конкретной информации о частоте среза схемы фильтра. Однако изучение взаимосвязи между частотой среза и кривой Найквиста является хорошим способом укрепить понимание концепции частоты среза в целом, а также даст нам некоторое представление об ограничениях подхода Найквиста для визуального изображения частотной характеристики.
Во-первых, нам нужно подумать о том, что на самом деле происходит на частоте среза, с точки зрения как амплитудно-частотной, так и фазо-частотной характеристики.
Частота среза относительно амплитуды
Вы, вероятно, знаете, что другое название для частоты среза – это «частота 3 дБ» (или –3 дБ), и это напоминает нам о том, что фильтр нижних частот первого порядка обеспечивает ослабление на 3 дБ (или, что эквивалентно, усилению –3 дБ), когда входная частота равна ω0. Мы не используем децибелы на графике Найквиста, поэтому вместо –3 дБ мы используем соответствующий коэффициент передачи в разах, который равен \(\frac{1}{\sqrt{2}}\)
Когда мы работаем с графиком в полярной системе координат, мы всегда должны помнить о треугольниках; например, амплитуда (модуль) комплексного числа определяется как гипотенуза прямоугольного треугольника, два катета которого являются действительной и мнимой частями; а для вычисления фазы (угла) комплексного числа мы используем тригонометрические функции. Теперь, когда вы думаете с точки зрения треугольников, коэффициент \(\frac{1}{\sqrt{2}}\) дает вам какие-нибудь идеи?
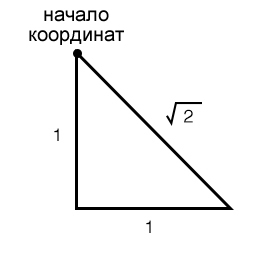
Как показано выше, коэффициент \(\sqrt{2}\) вступает в игру всякий раз, когда у прямоугольного треугольника два катета равной длины. Если уменьшить длину катетов до 0,5, длина гипотенузы будет равна \(\sqrt{2} \times 0,5\), что то же самое, что \(\frac{1}{\sqrt{2}}\).
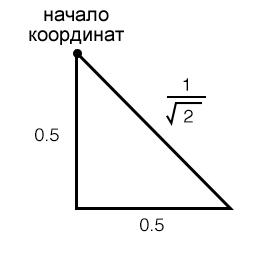
Итак, что же всё это значит? Рассмотрим следующий график Найквиста:
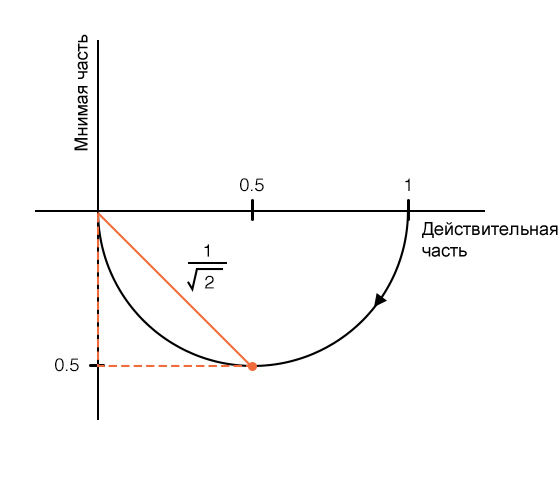
Как видите, в самой нижней точке кривой коэффициент усиления фильтра равен \(\frac{1}{\sqrt{2}}\), где абсолютное значение действительной части равно абсолютному значению мнимой части; это и есть местоположение частоты среза на графике Найквиста для фильтра нижних частот первого порядка. То же самое отношение применяется к фильтру верхних частот первого порядка, за исключением того, что в этом случае частота среза находится в самой высокой точке кривой:
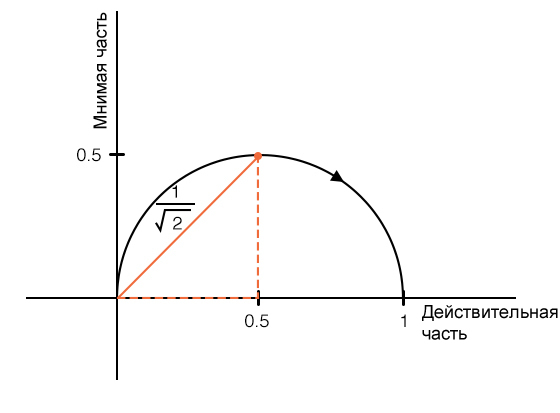
Разница заключается в том, что сдвиг фазы фильтра верхних частот с увеличением частоты изменяется от +90° до 0°, тогда как фаза фильтра нижних частот изменяется от 0° до –90°. Поскольку угол измеряется против часовой стрелки от положительной действительной оси, положительный сдвиг фазы отображается над действительной осью, а отрицательный сдвиг фазы отображается ниже действительной оси.
Также обратите внимание, что на этих двух графиках есть стрелки, указывающие в противоположных направлениях: на графике фильтра нижних частот стрелка указывает на начало координат, поскольку с увеличением частоты коэффициент усиления уменьшается; на графике фильтра верхних частот она указывает в сторону от начала координат, поскольку с увеличением частоты коэффициент усиления увеличивается.
Частота среза относительно сдвига фазы
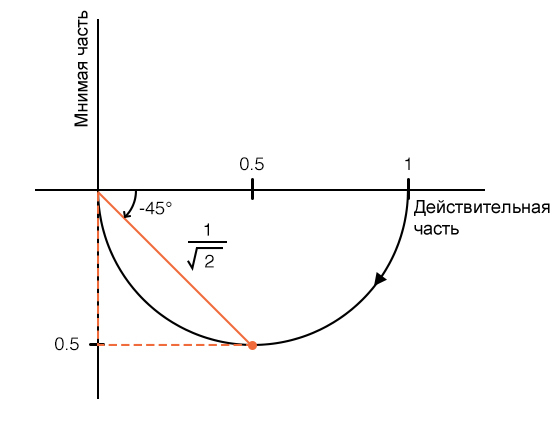
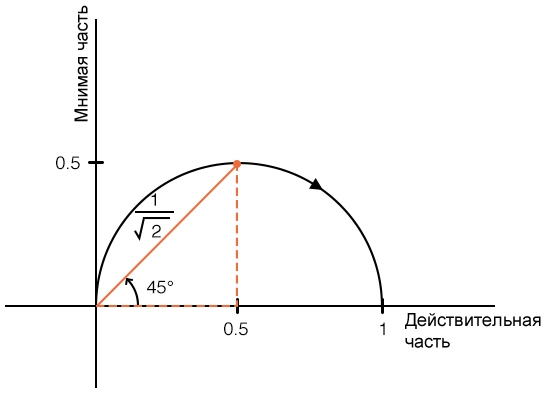
Мы также можем найти частоту среза на графике Найквиста, если вспомнить, что сдвиг фазы на 90°, создаваемый фильтром первого порядка, центрирован относительно частоты среза. Другими словами, фазовый сдвиг при ω0 составляет +45° или –45°. Вектор, нарисованный в комплексной плоскости, будет иметь угол +45° или –45°, если его действительная и мнимая части имеют одинаковые абсолютные значения, и это приводит нас к тем же геометрическим соотношениям, которые мы обнаружили при рассмотрении частоты среза с точки зрения амплитуды отклика.
Заключение
Возможно, вы заметили, что расположение частоты среза на этих графиках Найквиста является чисто геометрическим. Вы не можете прикрепить фиксированное значение частоты к этому местоположению, так как это местоположение одинаково для каждого фильтра нижних частот первого порядка или для каждого фильтра верхних частот первого порядка. Диаграмма Найквиста явно не является заменой для обычных логарифмических амплитудно-частотной и фазо-частотной характеристик. Но тем не менее, она дает более прямой способ передачи информации о передаточной функции системы, и, как мы увидим в следующей статье, это удобный инструмент для анализа устойчивости (стабильности).
