Как использовать диаграмму Найквиста (амплитудно-фазовую частотную характеристику) для частотного анализа
Данная статья познакомит вас с диаграммой Найквиста и объяснит, как интерпретировать этот альтернативный метод визуальной оценки частотной характеристики системы.
Большинство инженеров-электронщиков хорошо знакомы с графиками Боде (логарифмическими амплитудно-частотной и фазо-частотной характеристиками). Мы используем эти термины для обозначения графиков, на которых по горизонтальной оси откладывается частота в логарифмическом масштабе, а по вертикальной оси откладывается амплитуда (выраженная в децибелах) или фаза. Исходный график Боде представлял собой прямолинейную аппроксимацию реальной частотной характеристики системы, но в настоящее время мы используем этот термин и для математически точных графиков, генерируемых программным обеспечением для моделирования.
Однако существует другой метод визуального описания того, как система реагирует на разные входные частоты. Он называется графиком Найквиста (или диаграммой Найквиста) и используется в основном для анализа устойчивости. Он может быть менее интуитивно понятным, чем график Боде (логарифмические АЧХ и ФЧХ), но он более прямо указывает, будет ли усилитель устойчивым, и может одновременно передавать информацию об амплитуде и фазе.
Полярная система координат против декартовой системы координат
Диаграмма Найквиста – это график в полярной системе координат, и я думаю, что мы должны начать это обсуждение с краткого обзора концепции полярной системы координат.
Наиболее распространенный тип графика содержит независимую переменную, которая увеличивается вдоль горизонтальной оси, и зависимую переменную, которая выражается посредством изменения вертикального положения. Чтобы идентифицировать эту систему, которая передает информацию с помощью горизонтального и вертикального расстояния от двух осей, мы используем термин «декартовы координаты».
График в полярной системе координат, напротив, передает информацию, указывая амплитуду и угол. Амплитуда соответствует радиальному расстоянию от начала координат до любой точки кривой, а угол измеряется против часовой стрелки от положительной горизонтальной оси. На приведенной ниже диаграмме амплитуда обозначена как r, а угол – как θ.
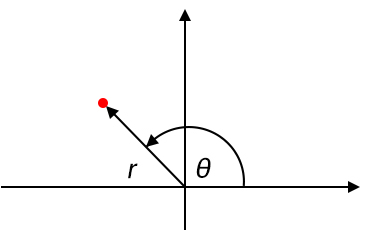
Комплексные числа
Поскольку графики в полярной системе координат по своей природе связаны с понятием пары значений, состоящей из амплитуды и угла, неудивительно, что они особенно полезны, когда мы работаем с комплексными числами. Комплексное число, выраженное в полярной форме, может быть сразу перенесено на график в полярной системе координат в виде амплитуды и угла, или мы можем использовать прямоугольную форму для определения местоположения точки, откладывая мнимую часть по вертикальной оси, а действительную часть – по горизонтальной оси.
Диаграмма Найквиста
Логарифмическая амплитудно-фазовая частотная характеристика (ЛАФЧХ, график Боде) передает значения амплитуды или фазы в зависимости от частоты. Таким образом, для описания амплитудно-частотного и фазо-частотного отклика системы вам нужны два графика (или, по крайней мере, вам нужны две кривые – вы можете включить две кривые в один график).
На диаграмме Найквиста, напротив, требуется только одна кривая. Это возможно, потому что график Найквиста является полярным: каждая точка на кривой указывает как амплитуду (через расстояние от начала координат), так и фазу (через геометрический угол), а многочисленные различные точки, которые образуют кривую, отражают реакцию системы на многочисленные различные входные частоты. Частота на графике Найквиста проходит от 0 до бесконечности, а для указания направления, в котором увеличивается частота, используется стрелка.
Я думаю, что будет намного понятнее после того, как мы рассмотрим пример. Следующая диаграмма – это график Найквиста для RC фильтра нижних частот первого порядка.
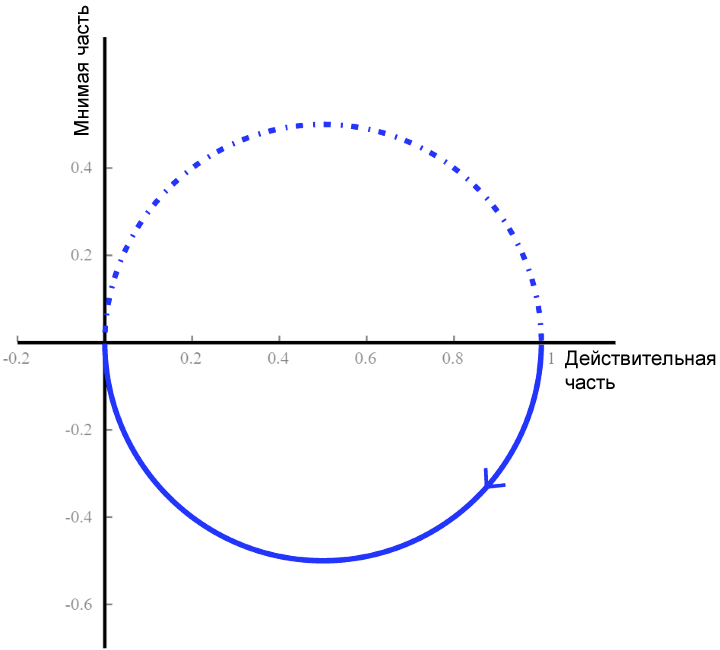
Давайте подробно рассмотрим этот график, чтобы убедиться, что мы понимаем, на что мы смотрим.
Наш пример диаграммы Найквиста
Вопрос: Прежде всего, почему на нем две кривые?
Ответ: Сплошная линия для положительных частот, а пунктирная линия для отрицательных частот. Они являются зеркальным отражением друг друга. Просто игнорируйте пунктирную линию.
Вопрос: Где находится информация о частоте?
Ответ: Помните, что кривая простирается от ω = 0 до ω = ∞, а стрелка указывает направление увеличения частоты. Таким образом, сплошная кривая начинается при ω = 0 с правой стороны графика (при значении 1 на оси действительных значений) и заканчивается в начале координат, что соответствует ω = ∞.
Вопрос: Хорошо, но как я должен интерпретировать этот полукруглый отклик по амплитуде?
Ответ: К счастью, мы уже знакомы с поведением RC фильтра нижних частот, поэтому давайте использовать эти знания, чтобы объяснить этот график Найквиста. В точке, где начинается кривая (т.е. при ω = 0), расстояние от начала координат равно 1. Другими словами, коэффициент передачи для низких частот, как и ожидалось, равен единице. По мере увеличения частоты радиальное расстояние от начала координат до кривой уменьшается – опять же, мы это ожидали, потому что меньшее радиальное расстояние соответствует большему затуханию. В точке, где кривая заканчивается (т.е. ω = ∞), расстояние от начала координат до кривой равно нулю, потому что, когда частота «достигает» бесконечности, фильтр нижних частот создает бесконечное затухание.
Вопрос: Это начинает обретать смысл. Я вижу, как изменение угла начинается от 0°, как и ожидалось, но фильтр нижних частот должен иметь конечный сдвиг фазы –90°. Как это отражено на диаграмме Найквиста? Я не могу измерить фазу точки, которая находится непосредственно над началом координат.
Ответ: Это, правда, немного сбивает с толку, но если вы сосредоточитесь на поведении кривой по мере приближения к началу координат, вы увидите, что угол стремится к –90°. Это показано на следующем графике, который также служит кратким изложением того, что мы только что рассмотрели.
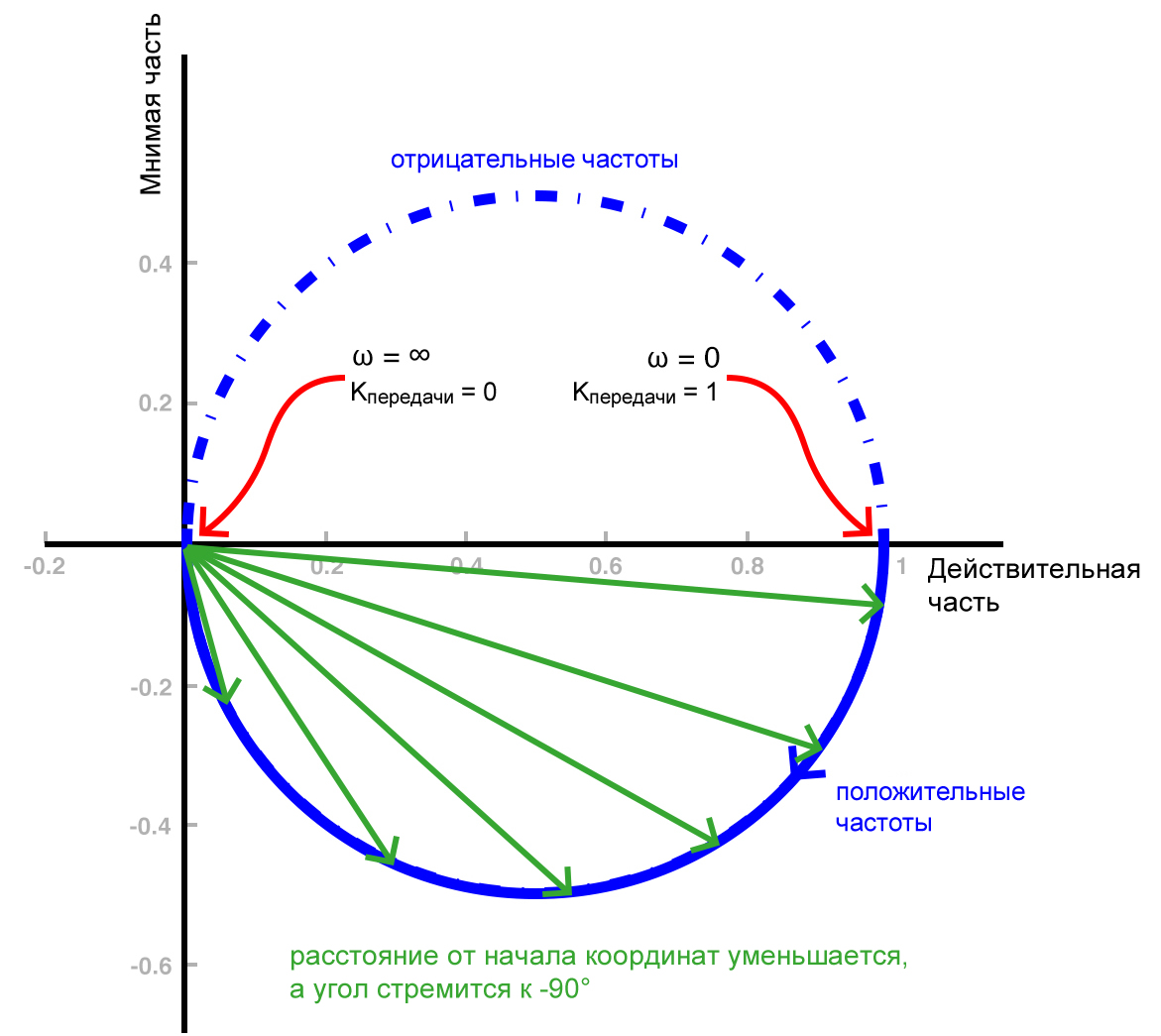
Заключение
Надеюсь, что теперь у вас есть четкое понимание самых основных характеристик диаграммы Найквиста. Мы рассмотрим эту тему подробнее в следующей статье.
