Диаграммы Найквиста для фильтров второго порядка
Данная статья продолжает серию статей о диаграммах Найквиста, объясняя графики Найквиста, которые представляют передаточную функцию двухполюсного фильтра.
В предыдущих статьях мы рассмотрели диаграмму Найквиста, а затем более детально исследовали этот тип диаграмм, изучив взаимосвязь между графиками Найквиста и частотой среза в отношении пассивных фильтров первого порядка. В этой статье мы рассмотрим графики Найквиста для фильтров второго порядка.
Обзор: Фильтры второго порядка
Когда я говорю «фильтр второго порядка», я имею в виду фильтры, которые используют для формирования истинной передаточной функции второго порядка резонанс индуктивности и конденсатора (LC) или усилитель. Вы можете получить двухполюсную частотную характеристику путем каскадного включения двух пассивных фильтров первого порядка, но результирующая схема не будет иметь комплексно-сопряженных полюсов, и, следовательно, передаточная функция не может быть оптимизирована, поскольку добротность всегда будет равна 0,5. В отличие от этого подхода, добротность фильтра второго порядка на основе резонанса или усилителя может контролироваться разработчиком таким образом, чтобы отдавать предпочтение плоской амплитудно-частотной характеристике в полосе пропускания, линейной фазовой характеристике или быстрому переходу от полосы пропускания к полосе задерживания.
Информация в этой статье относится к фильтрам второго порядка в целом, но, когда я писал статью, я имел в виду схему RLC фильтра нижних частот второго порядка, показанную ниже.
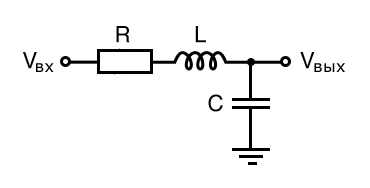
Частота среза этого фильтра определяется номиналами конденсатора и катушки индуктивности, а добротность можно корректировать, изменяя номинал резистора. Когда вы работаете с графиками Найквиста, важно помнить, что частота среза (ω0) фильтра второго порядка не обязательно равна «частоте -3 дБ». В зависимости от добротности фильтра усиление при ω0 может составлять -3 дБ, а может быть ниже -3 дБ или выше -3 дБ.
Квадранты на диаграмме Найквиста
Первое, что вы можете заметить на графике Найквиста для фильтра второго порядка, это то, что он заходит в нижний левый сектор комплексной плоскости. Например:
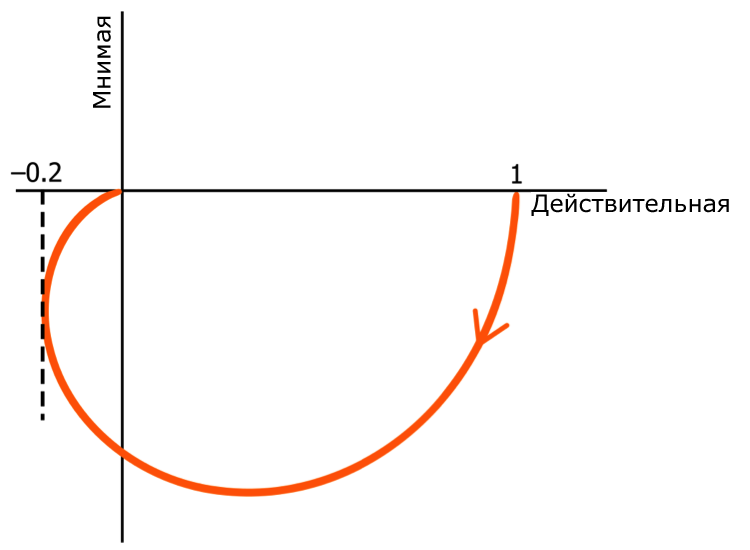
Обратите внимание, что все графики, показанные в данной статье, не включают отрицательные частоты.
Поскольку график заходит в нижний левый, а не в верхний левый квадрант, мы сразу знаем, что она представляет фильтр второго порядка. Почему? Итак, отрицательная мнимая ось соответствует сдвигу фазы -90°, и если график Найквиста пересекает эту ось и распространяется в нижний левый квадрант, фильтр должен иметь более одного полюса, потому что на каждый полюс вы получаете сдвиг фазы только -90°. У него не может быть трех полюсов, потому что угол не превышает -180° (что соответствует отрицательной действительной оси).
Вы можете видеть, что по мере приближения к началу координат кривая стремится к -180°, так же как сдвиг фазы двухполюсного фильтра стремится к -180° по мере увеличения частоты в сторону бесконечности.
Частота среза в фильтрах второго порядка
Как и в случае графиков Найквиста для фильтров первого порядка, график Найквиста для фильтра второго порядка не дает нам численное значение частоты среза. Однако в отличие от случая первого порядка, мы не можем найти обобщенное местоположение частоты среза, ища точку на кривой с откликом по амплитуде, равным \(\frac{1}{\sqrt{2}}\), потому что (как упоминалось выше) на коэффициент усиления при ω0 влияет добротность схемы.
Однако сдвиг фазы на частоте среза будет всегда составлять -90°, независимо от добротности. Таким образом, для фильтра нижних частот второго порядка частота среза соответствует точке, в которой график Найквиста пересекает отрицательную мнимую ось.
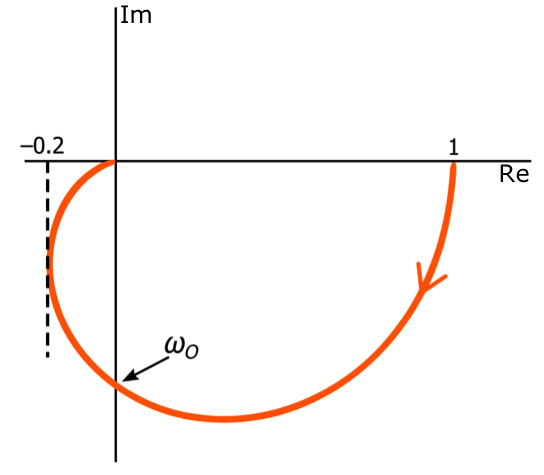
Добротность на диаграммах Найквиста для фильтров второго порядка
Даже базовые графики Найквиста, такие как показанные выше, могут дать нам важную качественную информацию о добротности фильтра второго порядка. Если мы знаем, что имеем дело с пассивным фильтром нижних частот, мы можем предположить, что коэффициент усиления на нижних частотах будет равен единице. Таким образом, график Найквиста начнется с амплитудного отклика, равного 1, и, поскольку сдвиг фазы на очень низких частотах, по сути, равен нулю, график Найквиста начинается от значения 1 на положительной части действительной оси.
Поведение графика после его ухода от действительной оси дает нам информацию об амплитудном отклике при увеличении частоты, а это, в свою очередь, дает нам информацию о добротности. Прежде всего, если расстояние от начала координат превышает исходное значение, то коэффициент усиления фильтра увеличивается по мере того, как частота входного сигнала приближается к частоте среза, и поэтому добротность должна быть достаточно высокой, чтобы вызвать появление некоторого пика.
Кроме того, вы можете сформировать общее представление о амплитудно-частотной характеристике в области частоты среза, сравнив коэффициент усиления на частоте среза с начальным коэффициентом усиления. Если усиление на частоте среза значительно выше, чем усиление на нижних частотах, вы знаете, что фильтр имеет относительно высокое значение добротности.
На следующем графике показаны два графика Найквиста для RLC фильтров с одинаковой частотой среза, но разной добротностью. Оранжевый график представляет собой фильтр с критическим затуханием (с ровной АЧХ с пологим склоном), т.е. Q = 0,5, а усиление при ω0 составляет -6 дБ. Синий график представляет фильтр не с критическим затуханием; его добротность составляет приблизительно 1,7, а усиление при ω0 составляет +4,7 дБ.
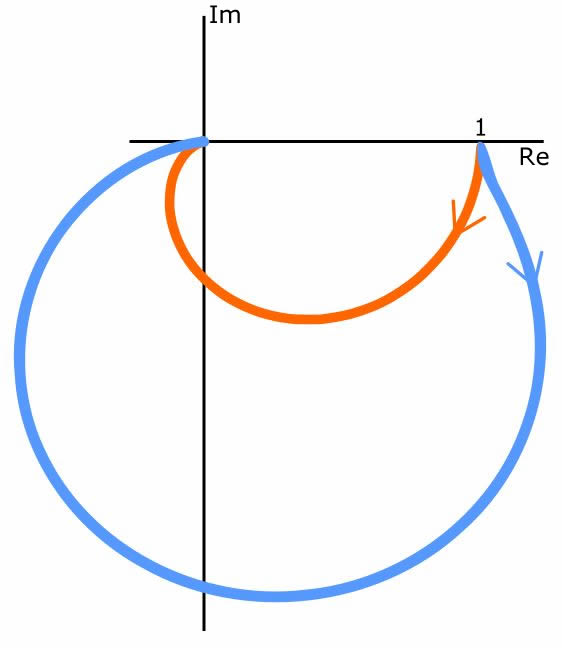
Заключение
Мы увидели, что диаграмма Найквиста для фильтра нижних частот дает нам четкую, прямую информацию о количестве полюсов в передаточной функции, и мы исследовали взаимосвязь между обобщенной формой графика Найквиста и добротностью фильтра второго порядка. В следующей статье мы продолжим наше обсуждение диаграмм Найквиста.
