Связь между временной и частотной областями представления сигналов
Электрические сигналы можно исследовать во временной области с помощью осциллографа и в частотной области с помощью анализатора спектра (рисунок 1).
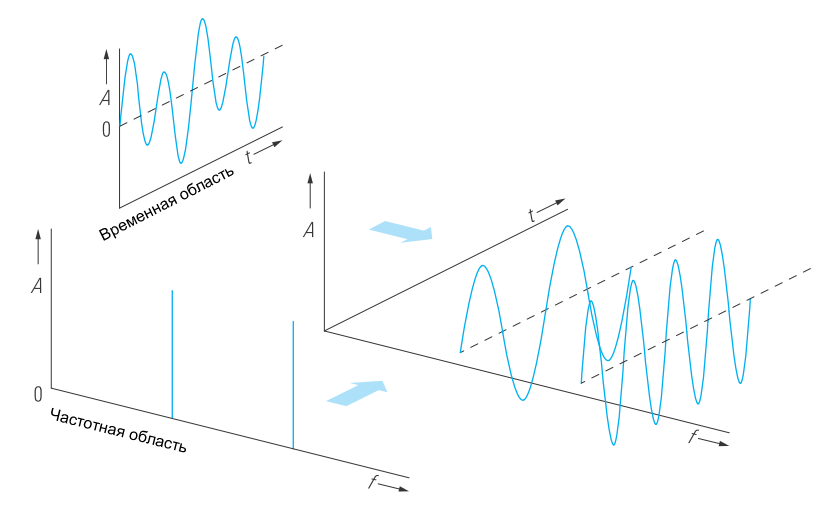
Эти два режима отображения сигналов связаны друг с другом преобразованием Фурье (обозначается как F), поэтому каждый сигнал во временной области имеет характерный частотный спектр. Таким образом, связь представлениями во временной и частотной областях будет следующей:
\[X_f (f) = F\{ x(t) \} = \int_{-\infty}^{+\infty}x(t) \cdot e^{-j2\pi ft} \ dt \qquad (1)\]
и
\[x(t) = F^{-1}\{X_f(f) \} = \int_{-\infty}^{+\infty}X_f(f) \cdot e^{j2\pi ft} \ df \qquad (2)\]
где
- \(F\{ x(t) \}\) – преобразование Фурье от \(x(t)\);
- \(F^{-1}\{X_f(f) \}\) – обратное преобразование Фурье от \(X_f (f)\);
- \(x(t)\) – сигнал во временной области;
- \(X_f (f)\) – комплексный сигнал в частотной области.
Чтобы проиллюстрировать эту взаимосвязь, сначала исследуем сигналы только с периодическим откликом во временной области.
Периодические сигналы
Согласно теореме Фурье любой сигнал, являющийся периодическим во временной области, может быть получен из суммы синусоидальных и косинусоидальных сигналов разной частоты и амплитуды. Такая сумма называется рядом Фурье. В этом случае применима следующая формула:
\[x(t) = \frac{A_0}{2} + \sum_{n=1}^{\infty} A_n \cdot \sin(n \cdot \omega_0 \cdot t) + \sum_{n=1}^{\infty} B_n \cdot \cos(n \cdot \omega_0 \cdot t) \qquad (3)\]
Коэффициенты Фурье A0, An и Bn зависят от формы сигнала x(t) и могут быть рассчитаны следующим образом:
\[A_0 = \frac{2}{T_0} \int_{0}^{T_0} x(t) \ dt \qquad (4)\]
\[A_n = \frac{2}{T_0} \int_{0}^{T_0} x(t) \cdot \sin(n \cdot \omega_0 \cdot t) \ dt \qquad (5)\]
\[B_n = \frac{2}{T_0} \int_{0}^{T_0} x(t) \cdot \cos(n \cdot \omega_0 \cdot t) \ dt \qquad (6)\]
На рисунке 2b показан прямоугольный сигнал, аппроксимированный в ряд Фурье. Отдельные компоненты этого ряда Фурье показаны на рисунке 2a. Чем больше этих компонентов, тем итоговый сигнал ближе к идеальным прямоугольным импульсам.

В случае синусоидальных или косинусоидальных сигналов для уравнения 1 можно найти решение в замкнутой форме, и для отображения комплексного спектра будут получены следующие соотношения:
\[F \{ \sin(2 \cdot \pi \cdot f_0 \cdot t) \} = \frac{1}{j} \cdot \delta (f-f_0) = -j \cdot \delta (f-f_0) \qquad (7)\]
и
\[F \{ \cos(2 \cdot \pi \cdot f_0 \cdot t) \} = \delta (f-f_0) \qquad (8)\]
где \(\delta (f-f_0)\) – функция Дирака:
\[\begin{equation*} \delta (f-f_0) = \begin{cases} \infty &\text{если } f-f_0=0 \ \text{, т.е. } f=f_0 \\\ 0 \end{cases} \end{equation*} \\ \int_{-\infty}^{+\infty} \delta (f-f_0) \ df = 1\]
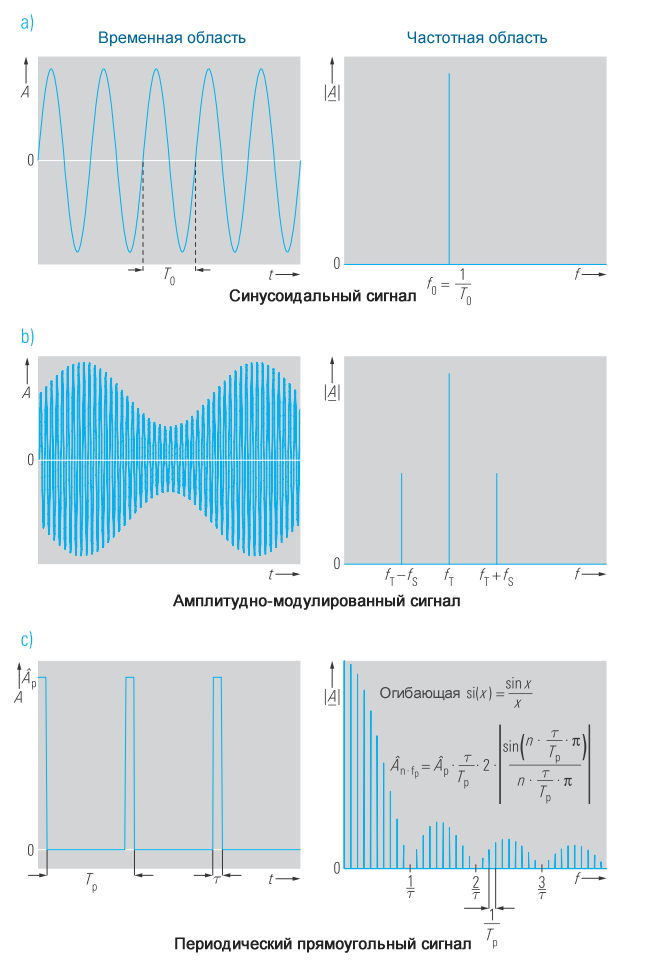
Можно видеть, что частотный спектр и синусоидального, и косинусоидального сигналов является функцией Дирака при f0 (смотрите рисунок 4a). Преобразования Фурье синусоидального и косинусоидального сигналов идентичны по величине, так что эти два сигнала демонстрируют идентичный амплитудный спектр на одной и той же частоте f0.
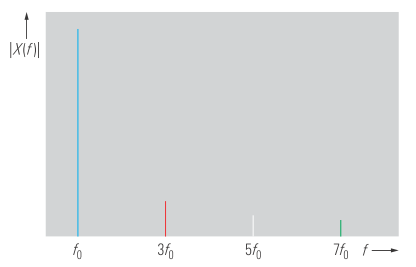
Чтобы вычислить частотный спектр периодического сигнала, временная характеристика которого описывается рядом Фурье в соответствии с уравнением 3, необходимо преобразовать каждый компонент ряда. Каждый из этих элементов приводит к функции Дирака, то есть дискретной составляющей в частотной области. Поэтому периодические сигналы всегда демонстрируют дискретные спектры, которые также называются линейчатыми спектрами. Например, спектр, показанный на рисунке 3, получен для аппроксимированного прямоугольного сигнала на рисунке 2.
На рисунке 4 показаны еще несколько примеров периодических сигналов во временной и частотной областях.
Непериодические сигналы
Сигналы с непериодическим поведением во временной области не могут быть описаны рядом Фурье. Следовательно, частотный спектр таких сигналов не может быть составлен из дискретных спектральных составляющих. Непериодические сигналы демонстрируют непрерывный частотный спектр с частотно-зависимой спектральной плотностью. Представление такого сигнала в частотной области вычисляется с помощью преобразования Фурье (уравнение 1).
Подобно синусоидальным и косинусоидальным сигналам, решение уравнения 1 в замкнутой форме может быть найдено для многих сигналов. Таблицы с такими парами преобразований можно найти в [1].
Для сигналов со случайными характеристиками во временной области, таких как шум или случайные битовые последовательности, решение в замкнутой форме встречается редко. В этом случае частотный спектр легче определить численным решением уравнения 1.
На рисунке 5 показаны некоторые непериодические сигналы во временной и частотной областях.
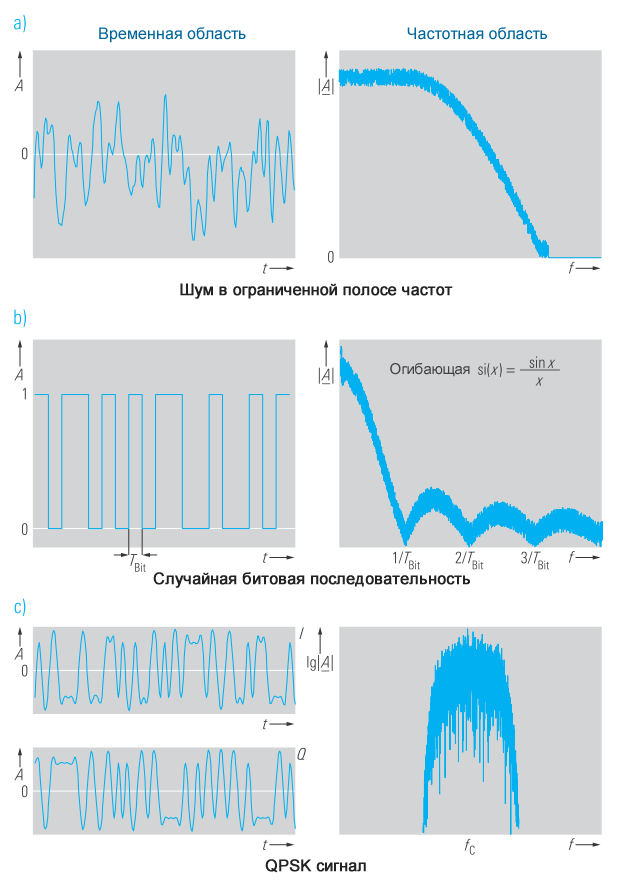
В зависимости от типа выполняемого измерения, полезными могут быть исследования либо во временной, либо в частотной области. Например, для измерения джиттера сигнала цифровой передачи данных требуется осциллограф. Для определения содержания гармоник более полезно исследовать сигнал в частотной области.
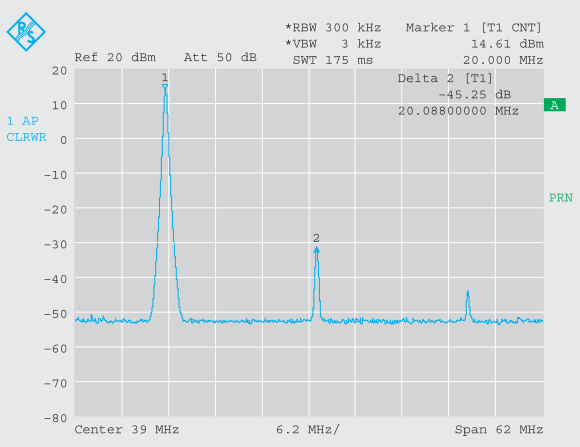
Сигнал, показанный на рисунке 6, кажется чистой синусоидой с частотой 20 МГц. Исходя из приведенных выше соображений, можно было бы ожидать, что его частотный спектр будет состоять только из одного компонента на частоте 20 МГц.
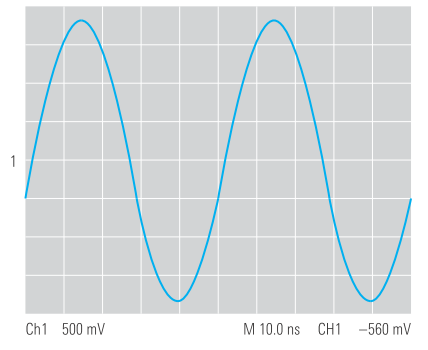
Однако при исследовании сигнала в частотной области с помощью анализатора спектра становится очевидным, что основная гармоника (гармоника 1-го порядка) накладывается на несколько гармоник более высокого порядка, то есть кратные 20 МГц (рисунок 7). Исследуя сигнал во временной области, эту информацию получить нелегко, и практическая количественная оценка высших гармоник невозможна. Кратковременную стабильность частоты и амплитуды синусоидального сигнала намного легче исследовать в частотной области, чем во временной (смотрите также раздел 6.1 «Измерение фазового шума).