Расчет электрической мощности

Формула расчета мощности

Мы видели формулу для определения мощности в электрической цепи: умножая напряжение в «вольтах» на ток в «амперах», мы получаем ответ в «ваттах». Давайте применим ее на примере схемы:

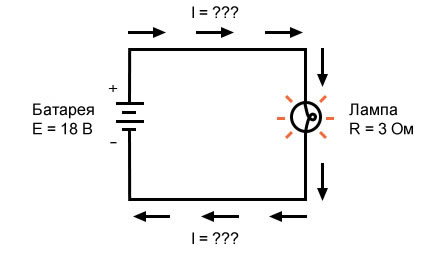
Как использовать закон Ома для определения силы тока

В приведенной выше схеме мы знаем, что у нас напряжение батареи 18 В и сопротивление лампы 3 Ом. Используя закон Ома для определения силы тока, мы получаем:

\[I = \frac{E}{R} = \frac{18 \ В}{3 \ Ом} = 6 \ А\]

Теперь, когда мы знаем силу тока, мы можем взять это значение и умножить его на напряжение, чтобы определить мощность:

\[P = IE = (6 \ А)(18\ В) = 108 \ Вт\]

Это говорит нам о том, что лампа рассеивает (выделяет) 108 Вт мощности, скорее всего, в виде света и тепла.

Увеличение напряжения батареи

Давайте попробуем взять ту же схему и увеличить напряжение батареи, чтобы посмотреть, что произойдет. Интуиция подсказывает нам, что с увеличением напряжения ток в цепи будет увеличиваться, а сопротивление лампы останется прежним. Таким же образом, увеличится и мощность:

Теперь напряжение аккумулятора составляет 36 вольт вместо 18 вольт. Лампа по-прежнему обеспечивает для прохождения тока электрическое сопротивление 3 Ом. Теперь сила тока равна:

\[I = \frac{E}{R} = \frac{36 \ В}{3 \ Ом} = 12 \ А\]

Это понятно: если I = E/R, и мы удваиваем E, а R остается прежним, сила тока тоже должна удвоиться. Так и есть: теперь у нас сила тока 12 ампер, вместо 6 А. А что насчет мощности?

\[P = IE = (12 \ А)(36\ В) = 432 \ Вт\]

Как повышение напряжения батареи влияет на мощность?

Обратите внимание, что мощность, как мы могли догадаться, увеличилась, но она увеличилась немного больше, чем ток. Почему? Поскольку мощность является функцией напряжения, умноженного на ток, а значения напряжения и силы тока увеличились в два раза по сравнению с их предыдущими значениями, мощность увеличится в 2 х 2, или в 4 раза. Вы можете проверить это, разделив 432 Вт на 108 Вт и увидев, что соотношение между ними действительно равно 4. Снова воспользовавшись алгеброй для манипуляции формулами, мы можем взять нашу исходную формулу мощности и изменить ее для случаев, где мы не знаем одновременно и напряжение, и силу тока, а знаем только напряжение (E) и сопротивление (R):

\[Если \qquad I=\frac{E}{R} \qquad и \qquad P=IE\]

\[То \qquad P=\frac{E}{R}E \qquad или \qquad P=\frac{E^2}{R}\]

Если мы знаем только ток (I) и сопротивление (R):

\[Если \qquad E=IR \qquad и \qquad P=IE\]

\[То \qquad P=I(IR) \qquad или \qquad P=I^2R\]

Закон Джоуля и закон Ома

Историческая справка: именно Джеймс Прескотт Джоуль, а не Георг Симон Ом, первым открыл математическую связь между рассеиваемой мощностью и током через сопротивление. Это открытие, опубликованное в 1841 году, имело форму последнего уравнения (P = I²R) и широко известно как закон Джоуля. Однако эти уравнения мощности настолько часто связаны с уравнениями закона Ома, связывающими напряжение, ток и сопротивление (E=IR; I=E/R и R=E/I), что их часто приписывают Ому.

\[P=IE \qquad P=\frac{E^2}{R} \qquad P=I^2R\]

Резюме

• Мощность измеряется в ваттах, которые обозначается как «Вт».
• Закон Джоуля: P = I²R; P = IE; P = E²/R

Теги