Что такое преобразование Фурье?
Данная статья даст вам важную информацию о математическом методе, который играет фундаментальную роль в проектировании систем и обработке сигналов.
Преобразование Фурье, названное в честь французского математика Жозефа Фурье, представляет собой математическую процедуру, которая позволяет нам определить частотный состав функции. Для инженеров-электронщиков преобразование Фурье обычно применяется к функциям времени, которые мы называем сигналами.
Разложение на синусоиды
График зависимости напряжения или тока от времени, который мы видим на экране осциллографа, представляет собой интуитивно понятное представление поведения сигнала. Однако это не единственное полезное представление.
Во многих случаях (например, при проектировании радиочастотных систем) нас в первую очередь интересует периодическое поведение сигналов. В частности, нас интересует понимание сигнала относительно синусоидальной периодичности, потому что синусоиды – это уникальное математическое выражение «чистой» частоты.
Преобразование Фурье выявляет элементарную периодичность сигнала, раскладывая этот сигнал на составляющие его синусоидальные частоты и определяя амплитуды и фазы этих составляющих частот.
Слово «разложение» здесь имеет решающее значение. Преобразование Фурье учит нас думать о сигнале во временной области как о сигнале, который состоит из базовых синусоидальных сигналов с различными амплитудами и фазами.
Например, прямоугольный сигнал может быть разложен на бесконечную последовательность синусоид с постоянно уменьшающимися амплитудами и постоянно увеличивающимися частотами. Точная последовательность для прямоугольного сигнала, с развязкой по постоянному току, с периодом T и амплитудой A, может быть записана следующим образом:
\[f_{прямоуг}(t)=\frac{4A}{\pi}\sum_{k\in{\{1,3,5,...\}}}\frac{1}{k}\sin\left(\frac{2\pi kt}{T}\right)\]
Мы можем преобразовать это в следующую форму, которая немного более интуитивна:
\[f_{прямоуг}(t)=\frac{4A}{\pi}\left(\sin(2\pi ft)+\frac{1}{3}\sin(6\pi ft)+\frac{1}{5}\sin(10\pi ft)+\ ...\right)\]
где f – частота прямоугольного сигнала в герцах.
На следующем графике синим цветом показан исходный прямоугольный сигнал и первые восемь синусоид в бесконечной последовательности.
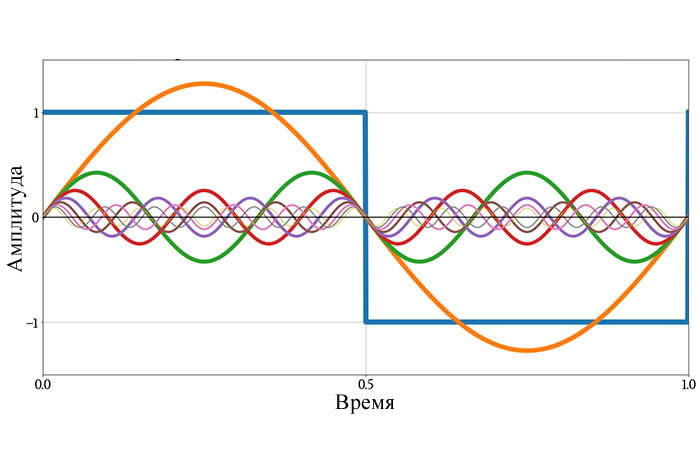
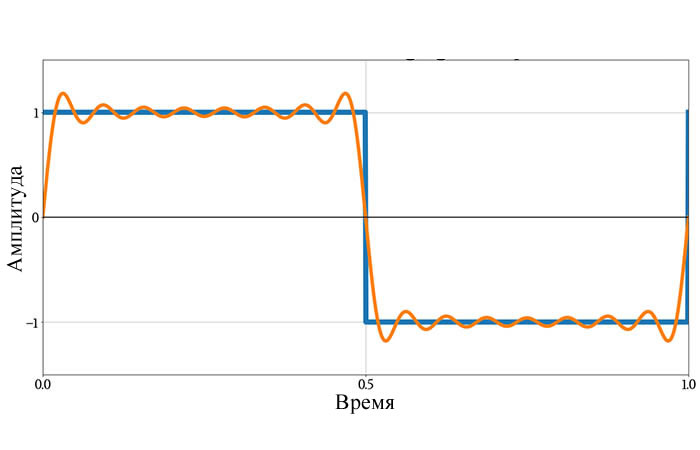
Посмотрев на этот график, вы всё еще можете немного скептически относиться к тому, что эти синусоиды можно объединить в прямоугольный сигнал. Но следующий график вас убедит. Он показывает исходный прямоугольный сигнал и форму сигнала, полученную путем сложения всех составляющих синусоид, показанных выше.
Функции времени и частоты
Когда мы вычисляем преобразование Фурье, мы начинаем с функции времени f(t), а с помощью математического разложения получаем функцию частоты F(ω) (обычно в теоретических обсуждениях преобразования Фурье мы используем угловую частоту).
Оценка функции F(ω) на некоторой определенной угловой частоте, скажем 100 рад/с, дает нам величину и фазу синусоидальной составляющей f(t), частота которой равна 100 рад/с. Если f(t) не имеет синусоидальной составляющей на 100 рад/с, то ее амплитуда будет равна нулю.
Вам может быть интересно, как одна функция F(ω) может говорить и об амплитуде, и о фазе. Преобразование Фурье создает комплексную функцию, что означает, что результат самого преобразования не является ни амплитудами частотных компонентов в f(t), ни фазами этих компонентов. Как и с любым комплексным числом, чтобы определить амплитуду или фазу, мы должны выполнить дополнительные вычисления.
Идея комплексного преобразования несколько более интуитивна, когда мы работаем с дискретным преобразованием Фурье, а не со «стандартным» преобразованием, в котором мы начинаем с символической функции времени и заканчиваем символической функцией частоты.
Дискретное преобразование Фурье работает с последовательностью числовых значений и создает последовательность коэффициентов Фурье. Эти коэффициенты – это типовые комплексные числа (т.е. они имеют форму a+jb), и обычно, при анализе частотных составляющих сигнала мы используем амплитуду этих комплексных чисел, вычисленную как \(\sqrt{a^2+b^2}\),.
Построение графика результатов преобразования Фурье
В технических описаниях, отчетах об испытаниях, учебниках и т.д. очень часто встречаются графики частотных составляющих. График зависимости амплитуды от частоты мы часто называем спектром – например, «давайте посмотрим на спектр сигнала» означает «давайте посмотрим на какое-то визуальное представление информации об амплитудах в результатах преобразования Фурье».
На следующем графике показан спектр прямоугольного сигнала, с развязкой по постоянному току, с амплитудой 1 и частотой 1 Гц.
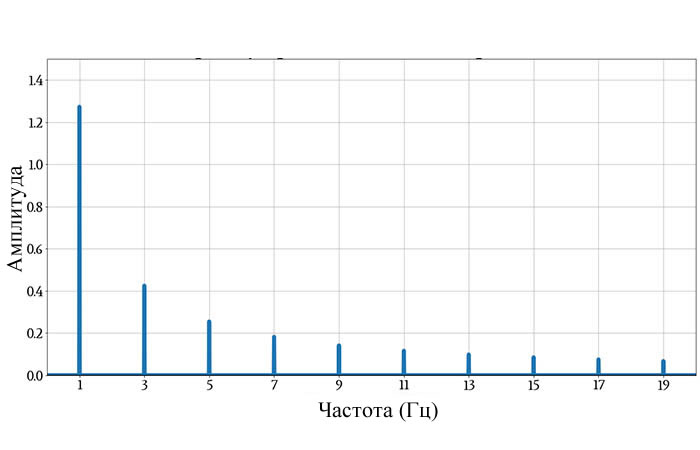
Если вы сравните нанесенные на график амплитуды частотных «всплесков» с амплитудами соответствующих синусоидальных составляющих в бесконечном ряду, описанном выше, то вы увидите, что они равны.
Вычисление преобразования Фурье
Мы почти подошли к концу этой статьи, и я все еще не рассказал вам, как мы на самом деле математически выполняем преобразование Фурье определенного сигнала.
Честно говоря, я не вижу необходимости тщательно исследовать математические подробности во вводной статье: в настоящее время в частотном анализе преобладают удобные для пользователя программные методы, а инженеры не тратят много времени на преобразование символического выражения во временной области в символическое выражение в частотной области.
Тем не менее, имея дело с чем-то важным, таким как преобразование Фурье, полезно, по крайней мере, иметь представление о математике, лежащей в его основе. Итак, без лишних слов, вот как мы преобразовываем f(t) в F(ω):
\[F(\omega ) = \int\limits_{ - \infty }^{ + \infty } {f(t){e^{ - j\omega t}}dt}\]
Заключение
Я надеюсь, что данная статья дала вам четкое, интуитивно понятное объяснение того, что такое преобразование Фурье и как оно дает нам дополнительное понимание сути сигнала.
Преобразование Фурье – это только начало обширного массива связанных тем. Если вы хотите узнать больше, ознакомьтесь со статьями, перечисленными ниже.
