Комплексно-сопряженные полюса в теории фильтров
В данном техническом обзоре объясняется важность комплексно-сопряженных полюсов и схем фильтров второго порядка относительно оптимизации производительности фильтров.
Связанная информация
Существует два способа получения частотной характеристики фильтра второго порядка (то есть двухполюсного): каскадно включить два фильтра первого порядка или использовать топологию схем второго порядка. Примером первого подхода являются два RC фильтра нижних частот, соединенных последовательно, при этом сигнал с выхода первого фильтра подается на второй фильтр через буфер из повторителя напряжения. Примерами второго подхода являются пассивные RLC фильтры и активные фильтры, такие как фильтр Саллена-Ки.
Конечно, это обсуждение также применимо к фильтрам более высокого порядка: четырехполюсная частотная характеристика может быть обеспечена четырьмя каскадами первого порядка или двумя каскадами второго порядка.
Есть привлекательная простота в подходе с каскадами первого порядка. Всё, что вам нужно для фильтра второго порядка, это немного простейшей математики, операционный усилитель, два резистора и два конденсатора (три, если вы хотите добавить блокировочный конденсатор для операционного усилителя). Почему тогда так много шума вокрух схем второго порядка? Что ж, ответ на этот вопрос приводит к важной концепции в теории фильтров: комплексно-сопряженные полюса.
Напомним, что сопряженные комплексные числа имеют действительные части, равные по величине и знаку, и мнимые части, равные по величине и противоположные по знаку. Давайте, визуализируем это с помощью s-плоскости:
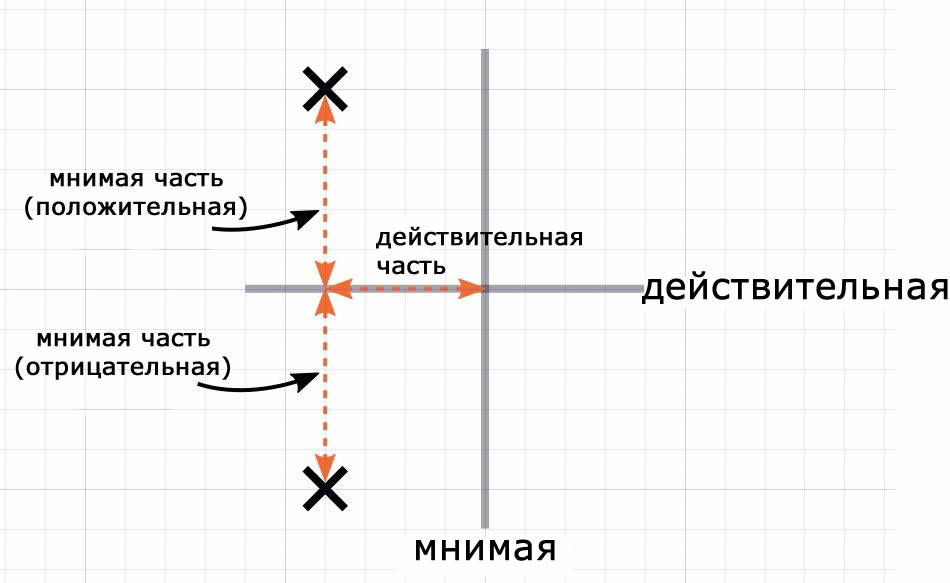
Здесь у нас комплексно-сопряженные полюса слева от мнимой оси (это там, где вы хотите, чтобы полюсы находились, если только вы не проектируете генератор вместо фильтра). Они имеют равное расстояние от действительной оси и от мнимой оси, но они являются отражениями относительно действительной оси, потому что у одного мнимая часть положительна, а у другого мнимая часть отрицательна.
Комплексно-сопряженные полюса важны, потому что они позволяют разработчику оптимизировать фильтр таким образом, чтобы он имел максимально плоскую полосу пропускания, быстрый переход от полосы пропускания к полосе задерживания или постоянную групповую задержку (то есть линейную фазовую характеристику). Проблема каскадного включения фильтров первого порядка заключается в том, что эта конфигурация не может обеспечить комплексно-сопряженные полюса.
Давайте рассмотрим этот факт на примере фильтра нижних частот с единичным усилением. Передаточная функция в s-области у него следующая:
\[H(s)=\frac{1}{s+\omega_0}\]
Каскадное включение двух таких фильтров соответствует произведению двух передаточных функций:
\[H(s)=\frac{1}{s+\omega_0}\times\frac{1}{s+\omega_0}=\frac{1}{s^2+2\omega_0 s+\omega_0^2}\]
Нас интересует 2ω0s. Знаменатель обобщенной передаточной функции второго порядка можно записать в виде
\[s^2+\frac{\omega_0}{Q} s+\omega_0^2\]
Таким образом, мы имеем
\[\frac{\omega_0}{Q}=2\omega_0 \ \Rightarrow \ Q = 0.5\]
Первое, на что следует обратить внимание, это то, что коэффициент Q не может быть подстроен так, чтобы точно настроить частотную характеристику. Два каскадно включенных фильтра первого порядка всегда будут иметь Q = 0,5 (кроме того, Q = 0,5 соответствует довольно плавному переходу от полосы пропускания к полосе задерживания и значительному затуханию в полосе пропускания).
Второе, что нужно понять, это то, что у вас не может быть комплексно-сопряженных полюсов, когда Q равен 0,5. Рассмотрим следующую диаграмму:

Расстояние от мнимой оси до полюса равно ω0/2Q, а расстояние от начала координат до полюса равно ω0 (ω0 – частота полюса). Если Q = 0,5, мы имеем ω0/(2 × 0,5) = ω0, и, таким образом, расстояние от мнимой оси будет равно расстоянию от начала координат. Отсюда следует, что полюс должен быть расположен на действительной оси, и, следовательно, нет возможности создания комплексно-сопряженной пары, поскольку местоположение полюса не имеет мнимой части.
Возможно, мы можем интуитивно сделать из схемы вывод, что каскадно включенные фильтры первого порядка не позволяют выполнить оптимизацию. Но полезно понимать, что эта жесткость связана с отсутствием комплексно-сопряженных полюсов, которые могут быть получены с использованием настоящего каскада второго порядка, и которые позволяют разработчику оптимизировать фильтр для конкретного приложения.
