Амплитудная модуляция: теория, временная и частотная области

Узнайте о самом простом способе кодирования информации в форме сигнала несущей частоты.

Мы видели, что радиочастотная модуляция представляет собой просто преднамеренную модификацию амплитуды, частоты или фазы синусоидального сигнала несущей частоты. Эта модификация выполняется в соответствии с конкретной схемой, которая реализуется передатчиком и понимается приемником. Амплитудная модуляция, которая, конечно, является источником термина «АМ радио», изменяет амплитуду несущей в соответствии с мгновенной величиной низкочастотного сигнала.

Математика

Математическое выражение амплитудной модуляции просто и интуитивно понятно: вы умножаете сигнал несущей на низкочастотный сигнал. Частота самой несущей не изменяется, но ее амплитуда будет постоянно изменяться в зависимости от величины низкочастотного сигнала. (Тем не менее, как мы увидим ниже, изменения амплитуды вводят новые частотные составляющие.) Здесь есть одна тонкая деталь – необходимость смещения низкочастотного сигнала; мы обсуждали это в предыдущей статье. Если у нас есть низкочастотный сигнал, который изменяется от -1 до +1, математическая зависимость может быть выражена следующим образом:

\[x_{ам}=x_{нес}(1+x_{нч})\]

где x_ам – амплитудно-модулированный сигнал, x_нес – сигнал несущей частоты, а x_нч – низкочастотный сигнал. Мы можем пойти дальше, если рассматривать несущую как бесконечную синусоиду с фиксированной частотой и постоянной амплитудой. Если предположить, что амплитуда несущей равна 1, мы можем заменить x_нес на sin(ω_несt).

\[x_{ам}(t)=\sin(\omega_{нес}t)(1+x_{нч}(t))\]

Пока всё хорошо, но есть одна проблема с этими связями: у вас нет контроля над «интенсивностью» модуляции. Другими словами, связь между изменением низкочастотного сигнала и изменением сигнала несущей частоты является фиксированной. Мы не можем, например, сконструировать систему таким образом, чтобы небольшое изменение в величине низкочастотного сигнала создавало значительное изменение амплитуды несущей. Чтобы устранить это ограничение, введем m, известный как индекс модуляции.

\[x_{ам}(t)=\sin(\omega_{нес}t)(1+mx_{нч}(t))\]

Теперь, изменяя m, мы можем контролировать интенсивность влияния низкочастотного сигнала на амплитуду несущей. Однако, обратите внимание, что m умножается на исходный, а не на смещенный низкочастотный сигнал. Таким образом, если x_нч изменяется от -1 до +1, любое значение m больше 1 приведет к тому, что (1 + mx_нч) будет заходить на отрицательный участок оси y, но это именно то, чего мы пытались избежать, сдвинув сперва низкочастотный сигнал вверх. Поэтому помните, что если используете индекс модуляции, сигнал должен быть смещен на максимальную амплитуду mx_нч, а не на x_нч.

Временна́я область

Мы рассмотрели формы амплитудно-модулированных сигналов во временно́й области в предыдущей статье. Последней была следующая диаграмма (низкочастотный сигнал – красный, амплитудно-модулированная несущая – синий):

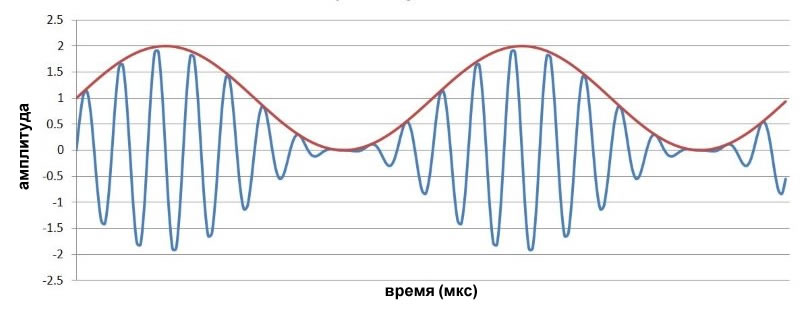
Теперь давайте посмотрим на влияние индекса модуляции. Вот аналогичный график, но на этот раз я сдвинул низкочастотный сигнал, добавив 3 вместо 1 (исходный размах всё еще составляет от -1 до +1).

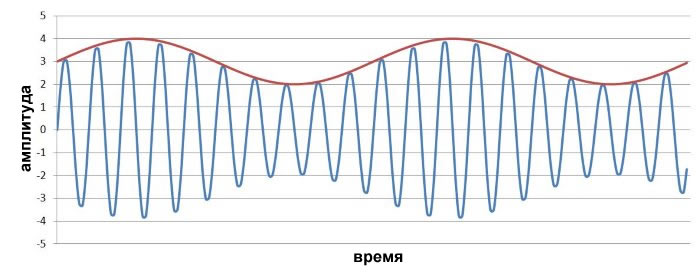
Теперь включим индекс модуляции. На следующем графике m = 3.

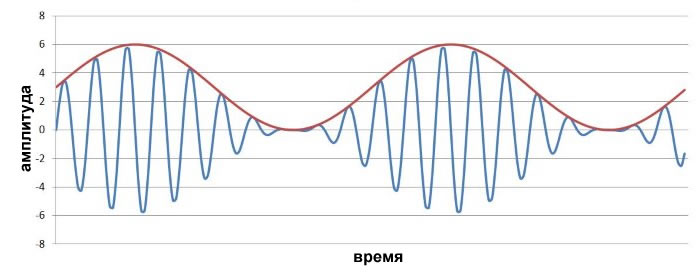
Амплитуда несущей теперь «более чувствительна» к изменению величины низкочастотного сигнала. Смещенный низкочастотный сигнал не заходит на отрицательную часть оси y, потому что я выбрал смещение по постоянному напряжению в соответствии с индексом модуляции.

Возможно, вам интересно, как выбрать правильное смещение по постоянному напряжению, не зная точных амплитудных характеристик низкочастотного сигнала? Другими словами, как мы можем гарантировать, что отрицательная волна низкочастотного сигнала доходит точно до нуля? Ответ: вам это не нужно. Предыдущие два графика являются одинаково допустимыми формами амплитудно-модулированного сигнала; низкочастотный сигнал корректно передается в обоих случаях. Любое смещение по постоянному напряжению, которое остается после демодуляции, легко удаляется с помощью последовательно включенного конденсатора (следующая глава будет посвящена демодуляции).

Частотная область

Как обсуждалось во второй статье данного миниучебника, радиочастотное проектирование широко использует анализ в частотной области. Мы может проверять и оценивать реальный модулированный сигнал, измеряя его с помощью анализатора спектра, но это означает, что нам нужно знать, как должен выглядеть спектр.

Начнем с представления сигнала несущей частоты в частотной области:

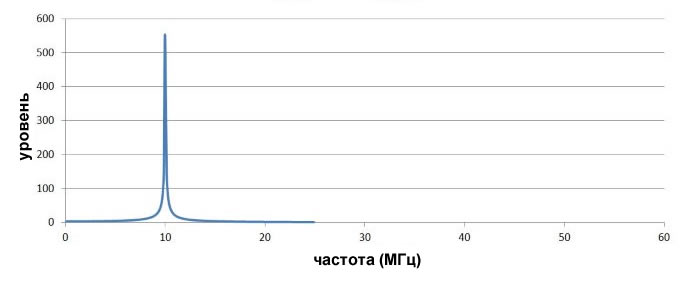
Это именно то, что мы ожидаем от немодулированной несущей: один всплеск на частоте 10 МГц. Теперь давайте посмотрим на спектр сигнала, создаваемого амплитудной модуляцией сигнала несущей частоты с помощью синусоиды с постоянной частотой 1 МГц.

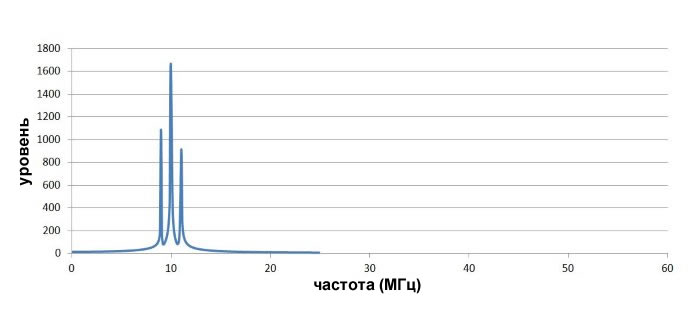
Здесь вы видите стандартные характеристики амплитудно-модулированного сигнала: низкочастотный сигнал сдвинут в соответствии с частотой несущей. Вы могли бы также подумать об этом как о «добавлении» частот низкочастотного сигнала к сигналу несущей, что мы и делаем, когда используем амплитудную модуляцию – несущая остается, как вы можете видеть на сигналах во временной области, но амплитудные изменения образовывают новые частотные составляющие, которые соответствуют спектральным характеристикам низкочастотного сигнала.

Если мы посмотрим более внимательно на спектр модулированного сигнала, то увидим, что два новых пика составляют 1 МГц (т.е. частота низкочастотного сигнала) выше и 1 МГц ниже несущей частоты:

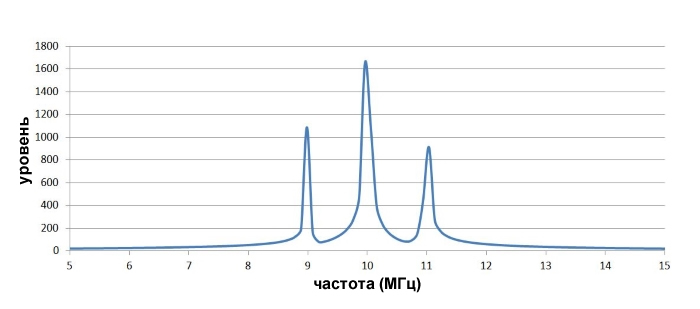
(В случае, если вам интересно, асимметрия является артефактом процесса вычисления, эти графики были созданы с использованием реальных данных и с ограниченным разрешением. Идеализированный спектр был бы симметричным.)

Отрицательные частоты

Резюмируя, амплитудная модуляция переносит спектр низкочастотного сигнала в полосу частот с центром на несущей частоте. Однако есть кое-что, что нам нужно объяснить: почему получилось два пика – один на несущей частоте плюс частота низкочастотного сигнала, а другой на несущей частоте минус частота низкочастотного сигнала? Ответ становится ясным, если мы просто вспомним, что спектр Фурье симметричен относительно оси y; хотя мы часто показывает только положительные частоты, отрицательная часть оси x содержит соответствующие отрицательные частоты. Эти отрицательные частоты легко игнорируются, когда мы имеем дело с исходным спектром, но при смещении спектра важно их учесть.

Следующая диаграмма должна прояснить эту ситуацию:

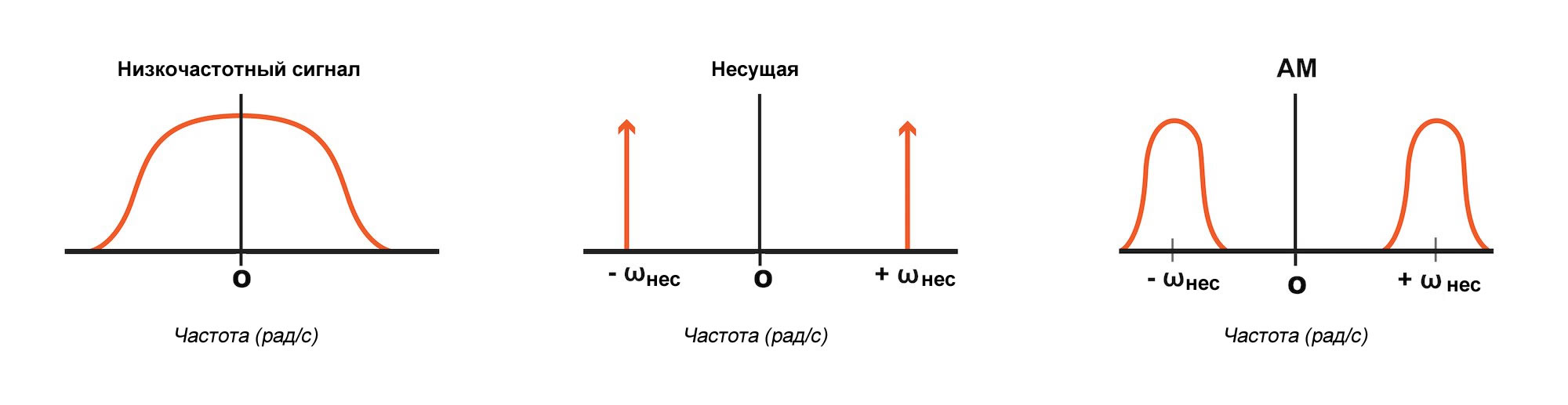
Как вы можете видеть, спектр низкочастотного сигнала и спектр несущей частоты симметричны относительно оси y. Для низкочастотного сигнала это приводит к спектру, который непрерывно продолжается от положительной части оси x до отрицательной часть, в случае несущей мы просто имеем два пика, один на +ω_нес и один на -ω_нес. И спектр амплитудно-модулированного сигнала, опять-таки, симметричный: перенесенный спектр низкочастотного сигнала появляется и в положительной, и в отрицательной частях оси x.

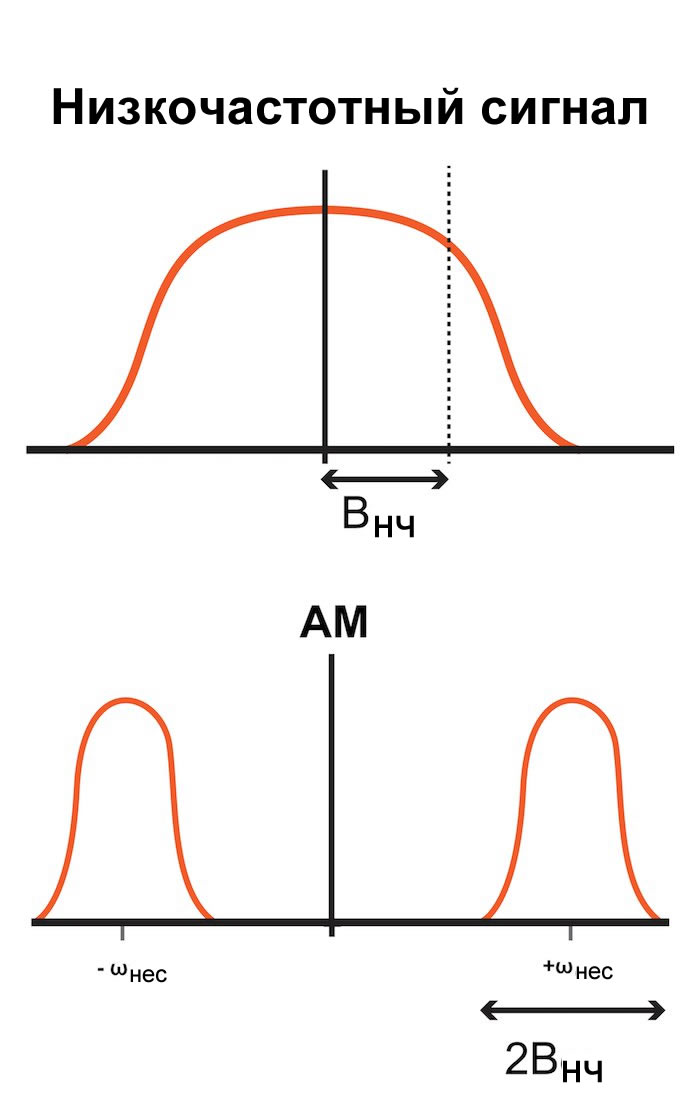
И еще одна вещь, которую следует иметь в виду: амплитудная модуляция увеличивает ширину полосы сигнала в два раза. Мы измеряем ширину полосы только для положительных частот, поэтому ширина полосы равна просто B_нч (смотрите диаграмму ниже). Но после переноса всего спектра (положительных и отрицательных частот), все исходные частоты становятся положительными, поэтому ширина полосы модулированного сигнала равна 2B_нч.

Резюме

• Амплитудная модуляция соответствует умножению сигнала несущей на смещенный низкочастотный сигнал.
• Индекс модуляции может использоваться, чтобы сделать амплитуду несущей более (или менее) чувствительной к изменениям величины низкочастотного сигнала.
• В частотной области амплитудная модуляция соответствует переносу спектра низкочастотного сигнала в полосу, окружающую несущую частоту.
• Поскольку спектр низкочастотного сигнала является симметричным относительно оси y, этот перенос частоты приводит к увеличению ширины полосы в 2 раза.

Теги