Квантовая физика
Думаю, можно сказать, что никто не понимает квантовую механику
Высказывание о том, что изобретение полупроводниковых приборов было революцией, не будет преувеличением. Это не только впечатляющее технологическое достижение, но оно также проложило путь для событий, которые навсегда изменяют современное общество. Полупроводниковые приборы применяются во всевозможных устройствах микроэлектроники, в том числе и в компьютерах, отдельных видах медицинского диагностического и лечебного оборудования, популярных телекоммуникационных устройствах.
Но за этой технологической революцией стоит даже больше, революция в общей науке: область квантовой теории. Без этого прыжка в понимании естественного мира, развитие полупроводниковых приборов (и более продвинутых разрабатываемых электронных устройств) никогда бы не удалось. Квантовая физика – это невероятно сложный раздел науки. В данной главе дается лишь краткий обзор. Когда ученые уровня Фейнмана говорят, что «никто не понимает [это]», вы можете быть уверены, что это действительно сложная тема. Без базового понимания квантовой физики или, по крайней мере, понимания научных открытий, которые привели к их разработке, невозможно понять, как и почему работают полупроводниковые электронные приборы. Большинство учебников по электронике пытаются объяснить полупроводники с точки зрения «классической физики», в результате делая их еще более запутанными для понимания.
Многие из нас видели диаграммы моделей атомов, которые похожи на рисунок ниже.
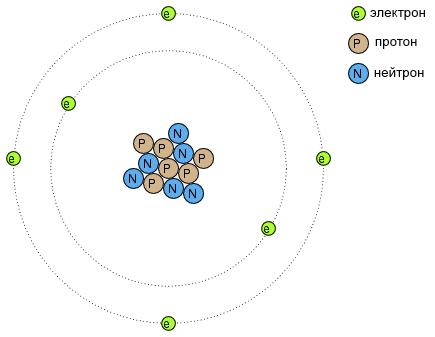
Крошечные частицы материи, называемые протонами и нейтронами, составляют центр атома; электроны вращаются как планеты вокруг звезды. Ядро несет положительный электрический заряд, благодаря наличию протонов (нейтроны не имеют никакого электрического заряда), в то время как уравновешивающий отрицательный заряд атома находится в движущихся по орбите электронах. Отрицательные электроны притягиваются к положительным протонам, как планеты притягиваются силой притяжения к Солнцу, однако орбиты стабильны, благодаря движению электронов. Мы обязаны этой популярной моделью атома работе Эрнеста Резерфорда, который примерно в 1911 году экспериментально определил, что положительные заряды атомов сосредоточены в крошечном, плотном ядре, а не равномерно распределены по диаметру, как ранее предполагал исследователь Дж. Дж. Томсон.
Эксперимент Резерфорда по рассеянию заключается в бомбардировке тонкой золотой фольги положительно заряженными альфа-частицами, как показано на рисунке ниже. Молодые аспиранты Х. Гейгер и Э. Марсден получили неожиданные результаты. Траектория движения некоторых альфа-частиц была отклонена на большой угол. Некоторые альфа-частицы были рассеяны в обратном направлении, под углом почти на 180°. Большинство частиц прошло через золотую фольгу, не изменив траекторию пути, будто фольги и не было совсем. Факт того, что несколько альфа-частиц испытывали большие отклонения в траектории движения, указывает на присутствие ядер с небольшим положительным зарядом.
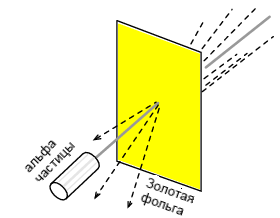
Хотя модель атома Резерфорда подтверждалась экспериментальными данными лучше, чем модель Томсона, она всё еще была неидеальна. Были предприняты дальнейшие попытки определения структуры атома, и эти усилия помогли проложить путь для странных открытий квантовой физики. Сегодня наше понимание атома немного сложнее. Тем не менее, несмотря на революцию квантовой физики и ее вклад в наше понимание строения атома, изображение солнечной системы Резерфорда в качестве структуры атом, прижилось в массовом сознании до такоей степени, что оно сохраняется в областях образования, даже если оно неуместно.
Рассмотрим это краткое описание электронов в атоме, взятое из популярного учебника по электронике:
Вращающиеся отрицательные электроны притягиваются к положительному ядру, которое приводит нас к вопросу о том, почему электроны не летят в ядро атом. Ответ в том, что вращающиеся электроны остаются на своей стабильной орбите из-за двух равных, но противоположных сил. Центробежная сила, действующая на электроны, направлена наружу, а сила притяжения зарядов пытается притянуть электроны к ядру.
В соответствии с моделью Резерфорда, автор считает электроны твердыми кусками материи, занимающими круглые орбиты, их притяжение внутрь к противоположно заряженному ядру уравновешивается их движением. Использование термина «центробежная сила» технически неверно (даже для вращающихся на орбитах планет), но это легко простить из-за популярного принятия модели: на самом деле, не существует такого понятия, как сила, отталкивающая любое вращающееся тело от центра его орбиты. Кажется, что это так потому, что инерция тела стремиться сохранить его движение по прямой линии, а так как орбита является постоянным отклонением (ускорением) от прямолинейного движения, есть постоянное инерционное противодействие к любой силе, притягивающей тело к центру орбиты (центростремительной), будь то гравитация, электростатическое притяжения, или даже натяжение механической связи.
Тем не менее, реальная проблема с этим объяснением, в первую очередь, заключается в идее электронов, движущихся по круговым орбитам. Проверенный факт, что ускоренные электрические заряды испускают электромагнитное излучение, этот факт был известен даже во времена Резерфорда. Так как вращательное движение является формой ускорения (вращающийся объект в постоянном ускорении, уводящем объект от нормального прямолинейного движения), электроны во вращающемся состоянии должны выбрасывать излучение, как грязь от буксующего колеса. Электроны, ускоренные по круговым траекториям, в ускорителях частиц, называемых синхротронами, как известно, делают это, и результат называется синхротронное излучение. Если бы электроны теряли энергию таким способом, их орбиты, в конечном счете, нарушились бы, и в результате они столкнулись бы с положительно заряженным ядром. Тем не менее, внутри атомов этого обычно не происходит. Действительно, электронные «орбиты» удивительно устойчивы в широком диапазоне условий.
Кроме того, эксперименты с «возбужденными» атомами показали, что электромагнитная энергия излучается атомом только на определенных частотах. Атомы «возбуждаются» внешними воздействиями, такими как свет, как известно, чтобы поглотить энергию и вернуть электромагнитные волны на определенных частотах, как камертон, который не звонит на определенной частоте, пока его не ударят. Когда свет, излучаемый возбужденным атомом, делится призмой на составные частоты (цвета), обнаруживаются отдельные линии цветов в спектре, картина спектральных линий является уникальной для химического элемента. Это явление обычно используется для идентификации химических элементов, и даже для измерения пропорций каждого элемента в соединении или химической смеси. Согласно солнечной системе атомной модели Резерфорда (относительно электронов, как кусков материи, свободно вращающихся на орбите с каким-то радиусом) и законам классической физики, возбужденные атомы должны вернуть энергию в практически бесконечном диапазоне частот, а не на избранных частотах. Другими словами, если модель Резерфорда была правильной, то не было бы эффекта «камертона», и цветовой спектр, излучаемый любым атомом, выглядел бы как непрерывная полоса цветов, а не как несколько отдельных линий.
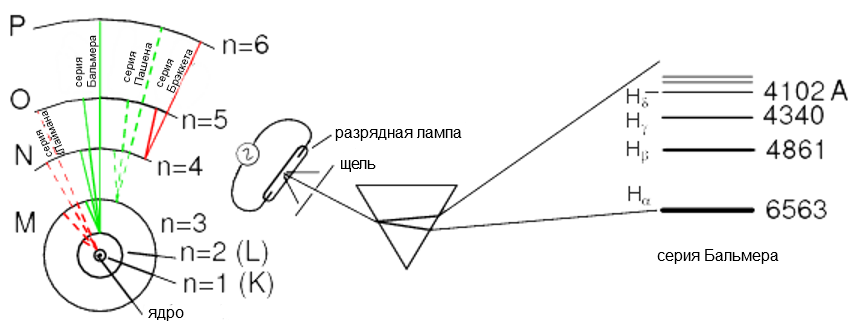
Исследователь по имени Нильс Бор попытался улучшить модель Резерфорда, после ее изучения в лаборатории Резерфорда в течение нескольких месяцев в 1912 году. Пытаясь согласовать результаты других физиков (в частности, Макса Планка и Альберта Эйнштейна), Бор предположил, что каждый электрон обладал определенным, конкретным количеством энергии, и что их орбиты распределяются таким образом, что каждый из них может занимать определенные места вокруг ядра, как шарики, зафиксированные на круговых дорожках вокруг ядра, а не как свободно двигающиеся спутники, как предполагалось ранее (рисунок выше). В знак уважения к законам электромагнетизма и ускоряющих зарядов Бор ссылался на «орбиты», как на стационарные состояния, чтобы избежать трактования, что они были подвижны.
Хотя амбициозная попытка Бора переосмысления строения атома, которое ближе согласовывалось с экспериментальными данными, и была важной вехой в физике, но не была завершена. Его математический анализ лучше предсказывал результаты экспериментов по сравнению с анализами, производимых согласно предыдущим моделям, но еще оставались без ответов вопросы о том, почему электроны должны вести себя таким странным образом. Утверждение, что электроны существовали в стационарных квантовых состояниях вокруг ядра, соотносилось с экспериментальными данными лучше, чем модель Резерфорда, но не говорило, что заставляет электроны принимать эти особые состояния. Ответ на этот вопрос должен был прийти от другого физика Луи де Бройля спустя примерно десять лет.
Де Бройль предположил, что электроны, как фотоны (частицы света), обладают и свойствами частиц, и свойствами волн. Опираясь на это предположение, он предположил, что анализ вращающихся электронов с точки зрения волн подходит лучше, чем с точки зрения частиц, и может дать больше понимания об их квантовой природе. И действительно, в понимании был совершен еще один прорыв.
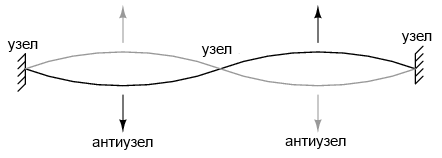
Атом, согласно де Бройлю, состоял из стоячих волн, явление, хорошо известное физикам в различных формах. Как дернутая струна музыкального инструмента (рисунок выше), вибрирующая на резонансной частоте, с «узлами» и «антиузлами» в стабильных местах вдоль своей длины. Де Бройль представил электроны вокруг атомов в виде волн, изогнутых в круг (рисунок ниже).
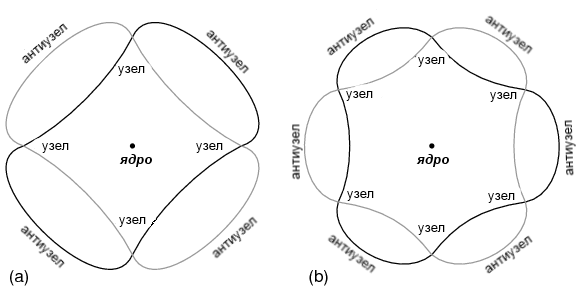
Электроны могут существовать только на определенных, конкретных «орбитах» вокруг ядра, потому что они являются единственными расстояниями, на которых концы волны совпадают. При любом другом радиусе волна будет разрушительно сталкиваться сама с собой и, таким образом, перестанет существовать.
Гипотеза де Бройля дала как математическое обеспечение, так и удобную физическую аналогию для объяснения квантовых состояний электронов внутри атома, но его модель атома была всё еще неполной. В течение нескольких лет физики Вернер Гейзенберг и Эрвин Шредингер, работая независимо друг от друга, трудились над концепцией корпускулярно-волнового дуализма де Бройля, чтобы создать более строгие математические модели субатомных частиц.
Этому теоретическому продвижению от примитивной модели стоячей волны де Бройля к моделям матрицы Гейзенберга и дифференциального уравнения Шредингера было дано название квантовая механика, она ввела довольно шокирующую характеристику в мир субатомных частиц: признак вероятности, или неопределенности. По новой квантовой теории, было невозможно определить точное положение и точный импульс частицы в один момент. Популярное объяснение этого «принципа неопределенности» заключалось в том, что существовала погрешность измерения (то есть, пытаясь точно измерить положение электрона, вы мешаете его импульсу, и, следовательно, не можете знать, что было до начала измерения положения, и наоборот). Сенсационный вывод квантовой механики заключается в том, что частицы не имеют точных положений и импульсов, и из-за связи этих двух величин их совокупная неопределенность никогда не уменьшится ниже определенного минимального значения.
Эта форма связи «неопределенности» существует и в других областях, кроме квантовой механики. Как обсуждалось в главе «Сигналы переменного тока смешанной частоты» тома 2 этой серии книг, есть взаимоисключающие связи между уверенностью в данных временной области формы сигнала и его данными в частотной области. Проще говоря, чем больше мы знаем его составляющие частоты, тем менее точно мы знаем его амплитуду во времени, и наоборот. Цитирую себя:
Сигнал бесконечной длительности (бесконечное количество циклов) может быть проанализирован с абсолютной точностью, но чем меньше циклов доступно компьютеру для анализа, тем меньше точность анализа... Чем меньше периодов сигнала, тем меньше точность его частоты. Принимая эту концепцию до ее логической крайности, короткий импульс (даже не полный период сигнала) на самом деле не имеет определенной частоты, представляет собой бесконечный диапазон частот. Данный принцип является общим для всех волновых явлений, а не только для переменных напряжений и токов.
Чтобы точно определить амплитуду изменяющегося сигнала, мы должны измерить его в очень короткий промежуток времени. Однако выполнение этого ограничивает наши знания о частоте волны (волна в квантовой механике не должна быть подобно синусоидальной волне; такое подобие является частным случаем). С другой стороны, чтобы определить частоту волны с большой точностью, мы должны измерять его в течение большого количества периодов, а значит, мы потеряем из виду его амплитуду в любой заданный момент. Таким образом, мы не можем одновременно знать мгновенную амплитуду и все частоты любой волны с неограниченной точностью. Еще одна странность, эта неопределенность гораздо больше неточности наблюдателя; она находится в самой природе волны. Это не так, хотя можно бы, учитывая соответствующие технологии, обеспечить точные измерения и мгновенной амплитуды, и частоты одновременно. В буквальном смысле, волна не может точную мгновенную амплитуду и точную частоту одновременно.
Минимальная неопределенность положения частицы и импульса, выраженная Гейзенбергом и Шредингером, не имеет ничего общего с ограничением в измерении; скорее это внутреннее свойство природы корпускулярно-волнового дуализма частицы. Следовательно, электроны на самом деле не существуют в своих «орбитах» как точно определенные частицы материи или даже как точно определенные формы волн, а скорее как «облака» – технический термин волновой функции распределения вероятности, как если бы каждый электрон был «рассеян» или «размазан» в диапазоне положений и импульсов.
Этот радикальный взгляд на электроны, как на неопределенные облака поначалу противоречит изначальному принципу квантовых состояний электронов: электроны существуют в дискретных, определенных «орбитах» вокруг ядра атома. Этот новый взгляд, в конце концов, был открытием, которое привело к образованию и объяснению квантовой теории. Как странно кажется, что теория, созданная для объяснения дискретного поведения электронов, заканчивается, объявив, что электроны существуют как «облака», а не как отдельные кусочки материи. Тем не менее, квантовое поведение электронов зависит не от электронов, имеющих определенные значения координат и импульса, а от других свойств, называемых квантовыми числами. В сущности, квантовая механика обходится без распространенных понятий абсолютного положения и абсолютного момента, а заменяет их абсолютными понятиями таких типов, у которых нет аналогов в общей практике.
Даже если электроны, как известно, существуют в бесплотных, «облачных» формах распределенной вероятности, а не в виде отдельных частей материи, эти «облака» имеют несколько другие характеристики. Любой электрон в атоме может быть описан четырьмя числовыми мерами (упомянутыми ранее квантовыми числами), которые называются главное (радиальное), орбитальное (азимутальное), магнитное и спиновое числа. Ниже представлен краткий обзор значения каждого из этих чисел:
Главное (радиальное) квантовое число: обозначается буквой n, это число описывает оболочку, на которой пребывает электрон. Электронная «оболочка» представляет собой область пространства вокруг ядра атома, на которой электроны могут существовать, соответствуя моделям стабильной «стоячей волны» де Бройля и Бора. Электроны могут «прыгать» с оболочки на оболочку, но не могут существовать между ними.
Главное квантовое число должно быть положительным целым числом (большим или равным 1). Другими словами, главное квантовое число электрона не может быть 1/2 или -3. Эти целые числа были выбраны не произвольно, а через экспериментальные доказательства светового спектра: разные частоты (цвета) света, излучаемые возбужденными атомами водорода, следуют математической зависимости, зависящей от конкретных целых значений, как показано на рисунке ниже.
Каждая оболочка обладает способностью удерживать несколько электронов. В качестве аналогии для электронных оболочек можно привести концентрические ряды сидений в амфитеатре. Так же, как человек, сидящий в амфитеатре, должен выбрать ряд, чтобы сесть (он не может сесть между рядов), электроны должны «выбрать» конкретную оболочку, чтобы «сесть». Как и ряды в амфитеатре, крайние оболочки удерживают больше электронов по сравнению с оболочками ближе к центру. Также электроны стремятся найти наименьшую доступную оболочку, как люди в амфитеатре ищут место, ближайшее к центральной сцене. Чем выше номер оболочки, тем больше энергии у электронов на ней.
Максимальное количество электронов, которое какая-либо оболочка может удерживать, описывается уравнение 2n2, где n – главное квантовое число. Таким образом, первая оболочка (n = 1) может содержать 2 электрона; вторая оболочка (n = 2) – 8 электронов; и третья оболочка (n = 3) – 18 электронов (рисунок ниже).
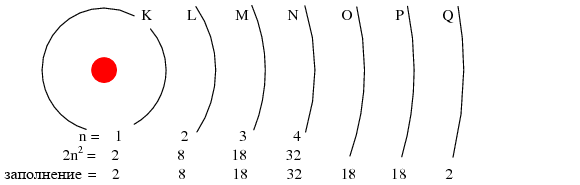
Электронные оболочки в атоме были обозначаются буквами, а не цифрами. Первая оболочка (n = 1) была обозначена K, вторая оболочка (n = 2) L, третья оболочка (n = 3) M, четвертая оболочка (n = 4) N, пятая оболочка (n = 5) O, шестая оболочка (n = 6) P, и седьмая оболочка (n = 7) B.
Орбитальное (азимутальное) квантовое число: оболочка, состоящая из подоболочек. Кому-то может быть удобнее думать о подоболочках как о простых секциях оболочек, как полосы делящие дорогу. Подоболочки гораздо более странны. Подоболочки – это области пространства, где могут существовать электронные «облака», и на самом деле различные подоболочки имеют различные формы. Первая подоболочка в форме шара (рисунок ниже (s)), который имеет смысл, когда визуализируется в виде электронного облака, окружающего ядро атома в трех измерениях.
Вторая подоболочка напоминает гантель, состоящую из двух «лепестков», соединенных в одной точке недалеко от центра атома (рисунок ниже (p)).
Третья подоболочка обычно напоминает набор из четырех «лепестков», сгруппированных вокруг ядра атома. Эти формы подоболочек напоминают графические изображения диаграмм направленности антенн с лепестками, похожими на луковицы, простирающимися от антенны в различных направлениях (рисунок ниже (d)).
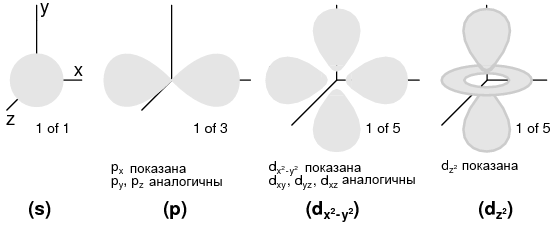
(s) трехкратная симметричность;
(p) Показана: px, одна из трех возможных ориентаций (px, py, pz), вдоль соответствующих осей;
(d) Показана: dx2-y2 похожа на dxy, dyz, dxz. Показана: dz2. Количество возможных d-орбиталей: пять.
Допустимыми значениями орбитального квантового числа являются положительные целые числа, как и для главного квантового числа, но также включают в себя ноль. Эти квантовые числа для электронов обозначаются буквой l. Количество подоболочек равно главному квантовому числу оболочки. Таким образом, первая оболочка (n = 1) имеет одну подоболочку с номером 0; вторая оболочка (n = 2) имеет две подоболочки с номерами 0 и 1; третья оболочка (n = 3) имеет три подоболочки с номерами 0, 1 и 2.
Старое соглашение описания подоболочек использовало буквы, а не цифры. А этом формате, первая подоболочка (l = 0) обозначалась s, вторая подоболочка (l = 1) обозначалась p, третья подоболочка (l = 2) обозначалась d, и четвертая подоболочка (l = 3) обозначалась f. Буквы пришли от слов: sharp, principal, diffuse и fundamental. Вы по-прежнему можете увидеть эти обозначения во многих периодических таблицах, используемые для обозначения электронной конфигурации внешних (валентных) оболочек атомов.
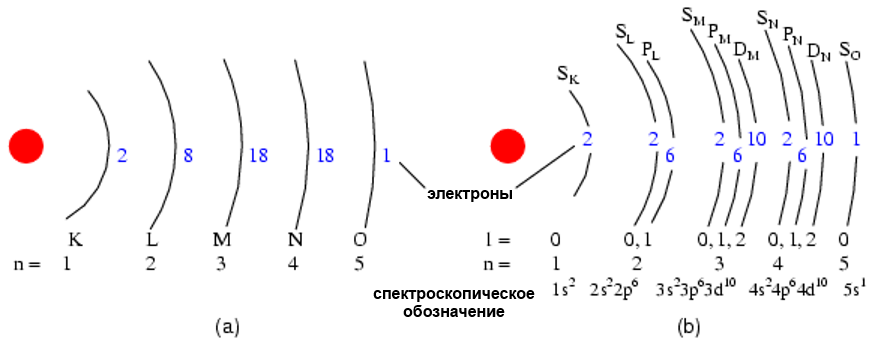
(b) орбитальное представление Ag с разделением оболочек на подоболочки (орбитальное квантовое число l).
Данная диаграмма не подразумевает ничего о фактическом положении электронов, а представляет только энергетические уровни.
Магнитное квантовое число: Магнитное квантовое число для электрона классифицирует, ориентацию фигуры подоболочки электрона. «Лепестки» подоболочек могут быть направлены в нескольких направлениях. Эти различные ориентации называются орбиталями. Для первой подоболочки (s; l = 0), которая напоминает сферу, «направление» не указывается. Для второй (p; l = 1) подоболочки в каждой оболочке, которая напоминает гантель, указывающую в трех возможных направлениях. Представьте три гантели, пересекающиеся в начале координат, каждая направлена вдоль своей оси в трехосной системе координат.
Допустимые значения для данного квантового числа состоят из целых чисел, начиная от -l до l, а обозначается данное число как ml в атомной физике и lz в ядерной физике. Чтобы рассчитать количество орбиталей в любой подоболочке, необходимо удвоить номер подоболочки и добавить 1, (2∙l + 1). Например, первая подоболочка (l = 0) в любой оболочке содержит одну орбиталь с номером 0; вторая подоболочка (l = 1) в любой оболочке содержит три орбитали с номерами -1, 0 и 1; третья подоболочка (l = 2) содержит пять орбиталей с номерами -2, -1, 0, 1 и 2; и так далее.
Как и главное квантовое число, магнитное квантовое число возникло прямо из экспериментальных данных: эффект Зеемана, разделение спектральных линий, подвергая ионизированный газ воздействию магнитного поля, отсюда и название «магнитное» квантовое число.
Спиновое квантовое число: как и магнитное квантовое число, данное свойство электронов атома было обнаружено с помощью экспериментов. Тщательное наблюдение спектральных линий показало, что каждая линия была на самом деле парой очень близко расположенных линий, было предположение, что эта так называемая тонкая структура была результатом каждого электрона, «вращающегося» вокруг своей оси, как планета. Электроны с разным «вращением» отдавали бы немного отличающиеся частоты света при возбуждении. Концепция вращающегося электрона в настоящее время устарела, будучи более подходящей для (неправильного) взгляда на электроны, как на отдельные частицы материи, а не как на «облака», но название осталось.
Спиновые квантовые числа обозначаются как ms в атомной физике и sz в ядерной физике. На каждой орбитали на каждой подоболочке в каждой оболочке может быть два электрона, один со спином +1/2, а другой со спином -1/2.
Физик Вольфганг Паули разработал принцип, объясняющий упорядоченность электронов в атоме в соответствии с этими квантовыми числами. Его принцип, называемый принципом запрета Паули, утверждает, что два электрона в одном атоме не могут занимать одинаковые квантовые состояния. То есть, каждый электрон в атоме имеет уникальный набор квантовых чисел. Это ограничивает число электронов, которые могут занимать какую-либо орбиталь, подоболочку и оболочку.
Здесь показано расположение электронов в атоме водорода:
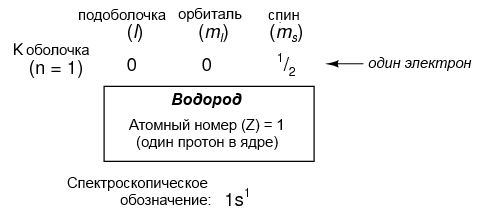
С одним протоном в ядре, атом принимает один электрон для своего электростатического баланса (положительный заряд протона в точности уравновешивается отрицательным зарядом электрона). Этот электрон находится на нижней оболочке (n = 1), первой подоболочке (l = 0), на единственной орбитали (пространственная ориентация) этой подоболочки (ml = 0), с значением спина 1/2. Общий метод описания этой структуры выполняется с помощью перечисления электронов в соответствии с их оболочками и подоболочками согласно соглашению, называемому спектроскопическим обозначением. В этом обозначении, номер оболочки показывается как целое число, подоболочка как буква (s,p,d,f), и общее количество электронов в подоболочке (все орбитали, все спины) как верхний индекс. Таким образом, водород с его единственным электроном, размещенным на базовом уровне, описывается как 1s1.
Переходя к следующему атому (по порядку атомного номера), мы получаем элемент гелий:
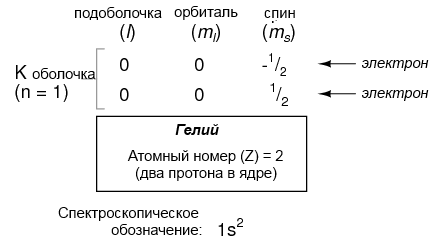
Атом гелия состоит из двух протонов в ядре, а это требует два электрона, чтобы сбалансировать двойной положительный электрический заряд. Так как два электрона – один со спином 1/2 и другой со спином -1/2 – находятся на одной орбитали, электронная структура гелия не требует дополнительных подоболочек или оболочек, чтобы удерживать второй электрон.
Тем не менее, атом, требующий три и более электрона, будет нуждаться в дополнительных подоболочках, чтобы удерживать все электроны, так как только два электрона могут находиться на нижней оболочке (n = 1). Рассмотрим следующий атом в последовательности увеличивающихся атомных номеров, литий:
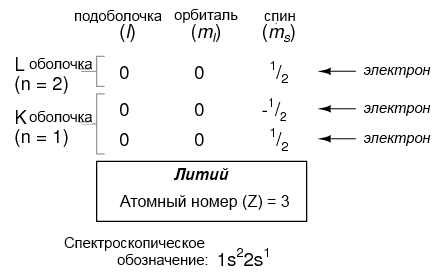
Атом лития использует часть емкости L оболочки (n = 2). Эта оболочка на самом деле имеет общую емкость величиной восемь электронов (максимальная емкость оболочки = 2n2 электронов). Если мы рассмотрим структуру атома с полностью заполненной L оболочкой, мы увидим, как все комбинации подоболочек, орбиталей и спинов заняты электронами:
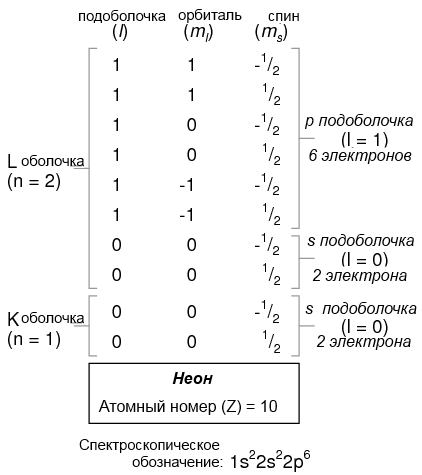
Часто, при назначении атому спектроскопического обозначения, любые полностью заполненные оболочки пропускаются, а не заполненные оболочки и заполненные оболочки высшего уровня обозначаются. Например, элемент неон (показан на рисунке выше), который имеет две полностью заполненных оболочки, может быть спектрально описан просто как 2p6, а не как 1s22s22p6. Литий с его полностью заполненной K-оболочкой и единственным электроном на L-оболочке, может быть описан просто как 2s1, а не 1s22s1.
Пропуск полностью заполненных оболочек нижнего уровня выполняется не только для удобства записи. Он также иллюстрирует основной принцип химии: химическое поведение элемента в первую очередь определяется его незаполненными оболочками. И водород, и литий обладают на своих внешних оболочках одним электроном (as1 и 2s1 соответственно), то есть, оба элемента обладают схожими свойствами. Оба обладают высокой реакционной способностью, и вступают в реакции почти одинаковыми способами (связывание с аналогичными элементами в аналогичных условиях). Не имеет большого значения, что литий имеет полностью заполненную K-оболочку под почти свободной L-оболочкой: незаполненная L-оболочка – это та оболочка, которая и определяет его химическое поведение.
Элементы, имеющие полностью заполненные внешние оболочки, классифицируются как благородные и отличаются почти полным отсутствием реакции с другими элементами. Эти элементы классифицировались как инертные, когда считалось, что они совсем не вступают в реакции, но, как известно, они образуют соединения с другими элементами при определенных условиях.
Так как элементы с одинаковыми конфигурациями электронов в своих внешних оболочках имеют сходные химические свойства, Дмитрий Менделеев соответственных образом организовал химические элементы в таблице. Данная таблица известна как периодическая таблица элементов, и современные таблицы следуют этому общему виду, показанному на рисунке ниже.
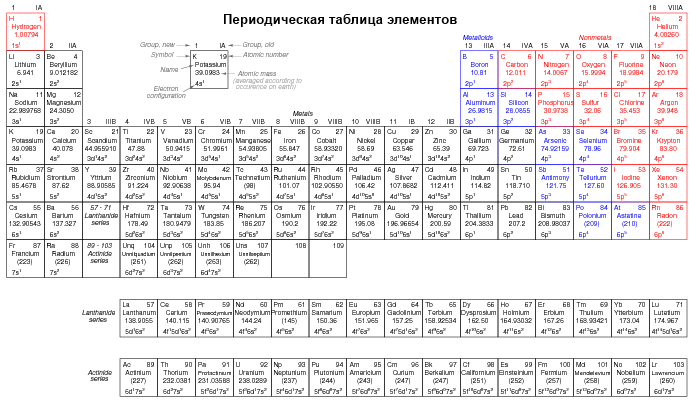
Дмитрий Менделеев, русский химик, был первым, кто разработал периодическую таблицу элементов. Несмотря на то, что Менделеев организовал свою таблицу в соответствии с атомной массой, а не атомным номером, и создал таблицу, которая была, не столь полезна, как современные периодические таблицы, его разработка выступает в качестве отличного примера научного доказательства. Увидев закономерности периодичности (аналогичные химические свойства в соответствии с атомной массой), Менделеев выдвинул гипотезу, что все элементы должны вписываться в эту упорядоченную схему. Когда он обнаружил «пустые» места в таблице, он следовал логике существующего порядка и предположил существование еще неизвестных элементов. Последующее открытие этех элементов подтвердило научную правильность гипотезы Менделеева, дальнейшие открытия привели к тому виду периодической таблицы, которую мы используем сейчас.
Вот так должна работать наука: гипотезы ведут к логическими заключениями и принимаются, изменяются или отклоняются в зависимости от согласованности экспериментальных данных с их выводами. Любой дурак может сформулировать гипотезу постфактум, чтобы объяснить имеющиеся экспериментальные данные, и многие так и делают. Что отличается научную гипотезу от спекуляции постфактум, так это предсказание будущих экспериментальных данных, которые пока не собраны, и, возможно, опровержение в результате этих данных. Смело ведите гипотезу к ее логическому заключению(-ям) и попытка предсказать результаты будущих экспериментов это не догматический прыжок веры, а скорее публичная проверка этой гипотезы, открытый вызов противникам гипотезы. Другими словами, научные гипотезы всегда «рискованны» из-за попытки предсказать результаты еще не проведенных экспериментов, и поэтому могут быть опровергнуты, если эксперименты пройдут не так, как ожидалось. Таким образом, если гипотеза правильно предсказывает результаты повторных экспериментов, ее ложность опровергнута.
Квантовая механика, сначала как гипотезы, а затем в качестве теории, оказалась чрезвычайно успешной в прогнозировании результатов экспериментов, следовательно, получила высокую степень научного доверия. У многих ученых есть основания полагать, что это неполная теория, так как ее прогнозы больше правдивы на микрофизических масштабах, а не в макроскопических размерах, но, тем не менее, это чрезвычайно полезная теория для объяснения и прогнозирования взаимодействия частиц и атомов.
Как вы уже увидели в этой главе, квантовая физика имеет важное значение при описании и прогнозировании множества различных явлений. В следующем разделе мы увидим, ее значение в электрической проводимости твердых веществ, в том числе и полупроводников. Проще говоря, ничего в химии или в физике твердого тела не имеет смысла в популярной теоретической структуре электронов, существующих как отдельные частицы материи, кружащиеся вокруг ядра атом, как миниатюрные спутники. Когда электроны рассматриваются как «волновые функции», существующие в определенных, дискретных состояниях, которые регулярны и периодичны, тогда поведение вещества может быть объяснено.
Подведем итоги
Электроны в атомах существуют в «облаках» распределенной вероятности, а не как дискретные частицы материи, вращающиеся вокруг ядра, как миниатюрные спутники, как показывают распространенные примеры.
Отдельные электроны вокруг ядра атом стремятся к уникальным «состояниям», описываемым четырьмя квантовыми числами: главное (радиальное) квантовое число, известное как оболочка; орбитальное (азимутальное) квантовое число, известное как подоболочка; магнитное квантовое число, описывающее орбиталь (ориентацию подоболочки); и спиновое квантовое число, или просто спин. Эти состояния квантовые, то есть «между ними» нет условий для существования электрона, кроме состояний, которые вписываются в схему квантовой нумерации.
Гланое (радиальное) квантовое число (n) описывает базовый уровень или оболочку, на которой находится электрон. Чем больше это число, тем больше радиус электронного облака от ядра атома, и тем больше энергия электрона. Главные квантовые числа являются целыми числами (положительными целыми)
Орбитальное (азимутальное) квантовое число (l) описывает форму электронного облака в конкретной оболочке или уровне и часто известно, как «подоболочка». В любой оболочке столько подоболочек (форм электронного облака), каково главное квантовое число оболочки. Азимутальные квантовые числа – целые положительные числа, начинающиеся с нуля и заканчивающиеся числом, меньшим главного квантового числа на единицу (n - 1).
Магнитное квантовое число (ml) описывает, какую ориентацию имеет подоболочка (фигура электронного облака). Подоболочки могут допускать столько различных ориентаций, чему равен удвоенный номер подоболочки (l) плюс 1, (2l+1) (то есть, для l=1, ml= -1, 0, 1), и каждая уникальная ориентация называется орбиталью. Эти числа – целые числа, начинающиеся от отрицательного значения номера подоболочки (l) через 0 и заканчивающиеся положительным значением номера подоболочки.
Спиновое квантовое число (ms) описывает другое свойство электрона и может принимать значения +1/2 и -1/2.
Принцип запрета Паули говорит, что два электрона в атоме не могут разделять один и тот же набор квантовых чисел. Следовательно, может быть не более двух электронов на каждой орбитали (спин=1/2 и спин=-1/2), 2l+1 орбиталей в каждой подоболочке, и n подоболочек в каждой оболочке, и не более.
Спектроскопическое обозначение – это соглашение для обозначения электронной структуры атома. Оболочки показываются как целые числа, за ними следуют буквы подоболочек (s, p, d, f) с числами в верхнем индексе, обозначающими общее количество электронов, находящихся в каждой соответствующей подоболочке.
Химическое поведение атома определяется исключительно электронами в незаполненных оболочках. Оболочки низкого уровня, которые полностью заполнены мало или совсем не влияют на химические характеристики связывания элементов.
Элементы с полностью заполненными электронными оболочками почти полностью инертны, и называются благородными элементами (ранее были известны как инертные).
