Понятие передаточной функции фильтра верхних частот первого порядка

Данная статья продолжает наше обсуждение передаточных функций в s-области и их роль в разработке и анализе аналоговых фильтров.

Если вы читали предыдущие статьи этой серии (о передаточных функциях фильтров нижних частот и полюсах и нулях), вы уже знакомы с различными важными понятиями, относящимися к анализу в s-области и к теории аналоговых фильтров. Давайте кратко пройдемся по ним:

• Мы можем создать выражение для поведения фильтра нижних частот при передаче сигнала от входа к выходу, проанализировав схему в s-области.
• Выражение V_вых/V_вх схемы является передаточной функцией фильтра, и если мы сравним это выражение с нормированной формой, мы сможем быстро определить два критических параметра, а именно частоту среза и максимальный коэффициент усиления (коэффициент передачи).
• Передаточная функция может быть записана в виде полинома числителя, деленного на полином знаменателя. Корни полинома числителя – это нули передаточной функции, а корни полинома знаменателя – полюсы передаточной функции. Другой способ сказать это: нули передаточной функции приводят к T(s) = 0, а полюсы передаточной функции приводят к T(s) → ∞.
• Полюсы приводят к тому, что наклон логарифмической амплитудно-частотной характеристики системы уменьшается на 20 дБ/декада; нули приводят к увеличению наклона на 20 дБ/декада.
• Полюсы дают сдвиг фазы -90°, а нули дают сдвиг фазы +90°.

Передаточная функция фильтра верхних частот

Схема RC фильтра верхних частот первого порядка реализована следующим образом:

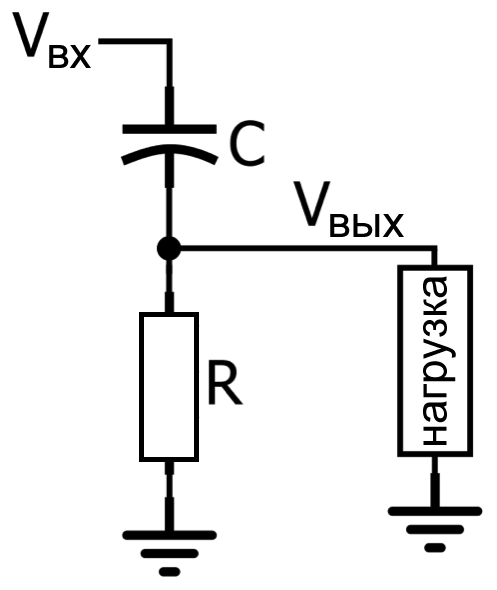
\[\frac{V_{вых}}{V_{вх}}=\frac{R}{\frac{1}{sC}+R}=\frac{sRC}{1+sRC}=\frac{s}{s+\frac{1}{RC}}\]

Поведение фильтра верхних частот первого порядка при передаче сигнала от входа к выходу можно описать с помощью следующей нормированной передаточной функции:

\[T(s)_{ФВЧ}=\frac{a_{1}s}{s+\omega _{0}}\]

Давайте сравним это с соответствующим выражением для фильтра нижних частот:

\[T(s)_{ФНЧ}=\frac{a_{0}}{s+\omega _{0}}\]

Как видите, знаменатели одинаковы. В обоих случаях мы имеем полюс при s = –ω₀, что означает, что и фильтр нижних частот, и фильтр верхних частот будут иметь следующие характеристики:

• уровень амплитудно-частотной характеристики при ω₀ будет на 3 дБ ниже максимального уровня АЧХ; для пассивного фильтра максимальный уровень АЧХ равен единице (0 дБ), а в случае при ω₀ значение составляет –3 дБ;
• абсолютное значение сдвига фазы цепи при ω₀ будет 45°.

Таким образом, выходной уровень при ω₀ в этих двух цепях очень похож. Однако на уровень АЧХ на частотах выше и ниже ω₀ влияет числитель T(s), и различие между этими двумя числителями в том, что делает фильтр нижних частот очень отличным от фильтра верхних частот.

Влияние числителя

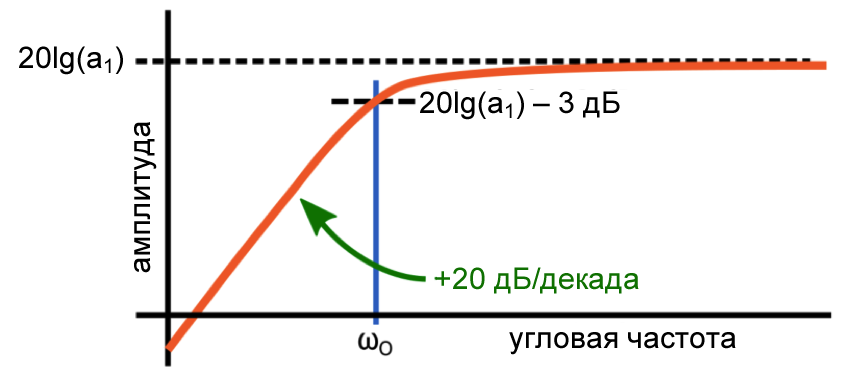
Числитель T(s) фильтра верхних частот говорит нам о двух вещах: начальный наклон АЧХ будет равен +20 дБ/декада, а максимальный уровень АЧХ будет равен a₁. Давайте подробнее рассмотрим эти две характеристики.

Начальный наклон

Поскольку теперь в числителе есть переменная s, у нас будет передаточная функция, равная нулю при любом значении s, при котором числитель будет равен нулю. В случае фильтра верхних частот первого порядка весь числитель умножается на s, поэтому ноль находится при s = 0.

Как ноль при s = 0 влияет на амплитудно-частотную и фазо-частотную характеристики реальной цепи? Во-первых, давайте рассмотрим АЧХ. Мы знаем, что ноль приведет к увеличению наклона кривой АЧХ на 20 дБ/декада. Однако это увеличение происходит при ω = 0 рад/с (или ƒ = 0 Гц), и здесь кроется ловушка: горизонтальная ось логарифмической амплитудно-частотной характеристики (диаграммы Боде) никогда не достигает 0 Гц. Это логарифмическая шкала, что означает, что частота уменьшается с 10 Гц до 1 Гц, до 0,1 Гц, до 0,01 Гц и так далее. Она никогда не достигает 0 Гц. Следовательно, мы никогда не видим угловую частоту нуля при ω = 0 рад/с.

Вместо этого кривая АЧХ просто начинается с наклона +20 дБ/декада. Выходной уровень продолжает увеличиваться до частоты полюса; полюс уменьшает наклон на 20 дБ/декада, в результате чего график АЧХ становится плоским (то есть наклон = 0 дБ/декада) и остается плоским при увеличении ω до бесконечности.

Максимальный коэффициент усиления

Всё, что нам нужно, это немного математических манипуляций, чтобы увидеть, что максимальный коэффициент усиления фильтра верхних частот будет равен a₁. Из общей формы амплитудно-частотной характеристики фильтра верхних частот мы знаем, что коэффициент усиления не может уменьшаться по мере увеличения ω до бесконечности. Таким образом, мы можем найти максимальный коэффициент усиления, определив T(s) при s → ∞. В знаменателе мы получаем s + ω₀. При добавлении чего-то к бесконечности мы получаем бесконечность, поэтому в этом случае мы можем упростить T(s) следующим образом:

\[T(s→∞)=\frac{a_{1}s}{s}\]

s в числителе и s в знаменателе сокращаются, поэтому

\[T(s→∞)=a_{1}\]

Фазо-частотная характеристика фильтра верхних частот

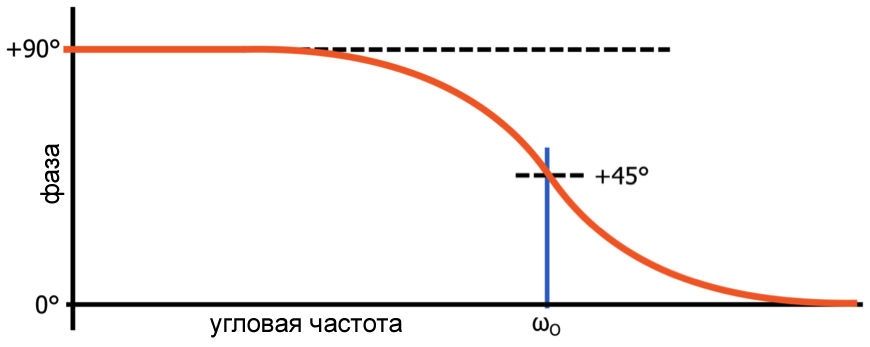
Как упоминалось ранее, ноль вносит в фазо-частотную характеристику системы сдвиг фазы +90°, при сдвиге фазы +45° на частоте нуля. Сдвиг фазы достигает +90° на частоте, которая на одну декаду выше частоты нуля, но фильтр верхних частот имеет ноль при ω = 0 рад/с, и вы не можете указать частоту, которая на одну декаду выше 0 рад/с – опять же, здесь мы имеем дело с логарифмической шкалой, которая означает, что горизонтальная ось никогда не достигнет 0 рад/с, и при этом она никогда не достигнет частоты, которая на одну декаду выше 0 рад/с (такая частота на самом деле не существует: 0 рад/с × 10 = 0 рад/с).

Результатом всего этого является то, что фазо-частотная характеристика фильтра верхних частот имеет начальное значение +90°. Другими словами, все низкочастотные входные сигналы будут смещены на +90°, а затем, по мере приближения частоты входного сигнала к частоте полюса, сдвиг фазы начинает уменьшаться:

Заключение

Мы рассмотрели стандартную передаточную функцию для фильтра верхних частот первого порядка и увидели, как эта передаточная функция приводит к амплитудно-частотной и фазо-частотной характеристикам.

В следующей статье мы увидим, что передаточную функцию фильтра нижних частот и передаточную функцию фильтра верхних частот можно объединить в общую передаточную функцию первого порядка, а также кратко рассмотрим полосовой фильтр первого порядка.

Теги