Сигналы прямоугольной формы

Было обнаружено, что любой повторяющийся несинусоидальный сигнал может быть приравнен к комбинации постоянного напряжения, синусоидальных сигналов и/или косинусоидальных сигналов (синусоидальных сигналов со сдвигом фазы на 90 градусов) с различными амплитудами и частотами. Это верно, независимо от того, насколько странной или запутанной может быть форма рассматриваемого сигнала. До тех пор, пока он регулярно повторяется с течением времени, он сводится к этой последовательности синусоидальных сигналов. В частности, было обнаружено, что прямоугольные сигналы математически эквивалентны сумме синусоидального сигнала на той же частоте плюс бесконечный ряд синусоидальных сигналов с нечетными кратными частотами и уменьшающейся амплитудой:

\[\text{повторяющийся прямоугольный сигнал 1 В (пик), 50 Гц эквивалентен:}\\ \left(\frac{4}{\pi}\right) (\text{синусоидальный сигнал 1 В (пик), 50 Гц})\\ + \left(\frac{4}{\pi}\right) (\text{синусоидальный сигнал 1/3 В (пик), 150 Гц})\\ + \left(\frac{4}{\pi}\right) (\text{синусоидальный сигнал 1/5 В (пик), 250 Гц})\\ + \left(\frac{4}{\pi}\right) (\text{синусоидальный сигнал 1/7 В (пик), 350 Гц})\\ + \left(\frac{4}{\pi}\right) (\text{синусоидальный сигнал 1/9 В (пик), 550 Гц})\\ + \text{... и далее до бесконечности ...}\]

Эта правда о сигналах на первый взгляд может показаться слишком странной, чтобы в нее поверить. Однако, если прямоугольный сигнал на самом деле представляет собой бесконечный ряд гармоник синусоидального сигнала, сложенных вместе, само собой разумеется, мы должны быть в состоянии доказать это, сложив вместе несколько гармоник синусоидального сигнала, чтобы получить близкое приближение к прямоугольному сигналу. Эти рассуждения не только просто звучат, но и легко демонстрируются с помощью SPICE.

Схема, которую мы будем моделировать, представляет собой не что иное, как несколько источников синусоидального переменного напряжения правильных амплитуд и частот, соединенных последовательно. Мы будем использовать SPICE для построения графиков колебаний напряжения между последовательными сложениями источников напряжения, например:

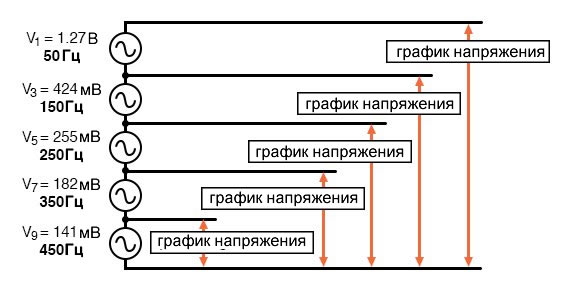
В этом конкретном моделировании SPICE я суммировал источники напряжения 1-й, 3-й, 5-й, 7-й и 9-й гармоник последовательно для всего пяти источников переменного напряжения. Основная частота составляет 50 Гц, и каждая гармоника, конечно, является целым кратным этой частоты. Значения амплитуды (напряжения) не являются случайными числами; они были получены с помощью уравнений, показанных в частотном ряду (дробь 4/π, умноженная на 1, 1/3, 1/5, 1/7 и т. д. для каждой из последующих нечетных гармоник).

building a squarewave 
v1 1 0 sin (0 1.27324 50 0 0)       1st harmonic (50 Hz)
v3 2 1 sin (0 424.413m 150 0 0)     3rd harmonic
v5 3 2 sin (0 254.648m 250 0 0)     5th harmonic
v7 4 3 sin (0 181.891m 350 0 0)     7th harmonic
v9 5 4 sin (0 141.471m 450 0 0)     9th harmonic
r1 5 0 10k      
.tran 1m 20m    
.plot tran v(1,0)    Plot 1st harmonic    
.plot tran v(2,0)    Plot 1st + 3rd harmonics
.plot tran v(3,0)    Plot 1st + 3rd + 5th harmonics
.plot tran v(4,0)    Plot 1st + 3rd + 5th + 7th harmonics
.plot tran v(5,0)    Plot 1st + . . . + 9th harmonics
.end

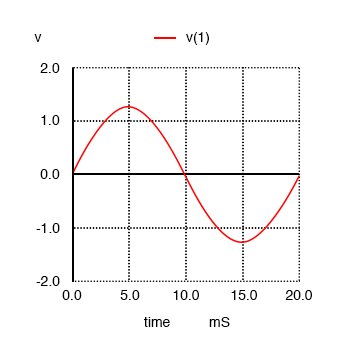
Начиная отсюда, я расскажу об этом анализе шаг за шагом, объясняя, на что мы видим. На первом графике мы видим синусоидальный сигнал основной частоты 50 Гц сам по себе. Это не что иное, как чистая форма синуса, без дополнительного гармонического содержания. Это форма сигнала, создаваемого идеальным источником переменного напряжения:

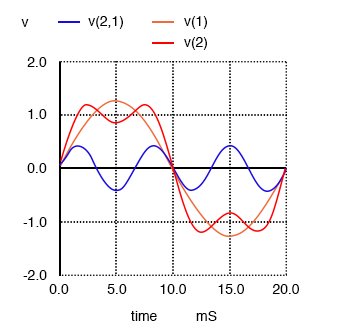
Далее мы видим, что происходит, когда этот чистый и простой сигнал объединяется с третьей гармоникой (три раза по 50 Гц или 150 Гц). Внезапно это уже не похоже на чистую синусоидальную волну:

Время нарастания и спада между положительным и отрицательным интервалами теперь намного меньше, наклон круче, а вершины сигнала ближе к тому, чтобы стать плоскими, как прямоугольный сигнал. Посмотрите, что происходит, когда мы добавляем следующую частоту нечетной гармоники:

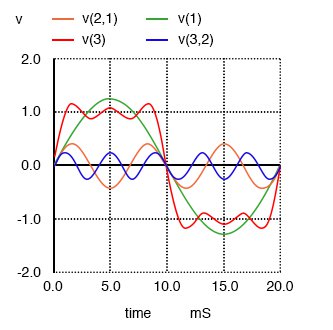
Наиболее заметным изменением здесь является то, как вершины сигнала сгладились еще больше. На каждой вершине сигнала стало больше провалов и пиков, но эти провалы и пики имеют меньшую амплитуду, чем было раньше. Посмотрите еще раз, как мы добавляем сигнал следующей нечетной гармоники:

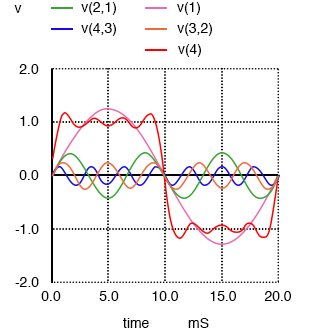
Здесь мы видим, как сигнал становится более плоским на каждой вершине. Наконец, добавив в нашу схему 9-ю гармонику, пятый источник синусоидального напряжения, мы получим следующий результат:

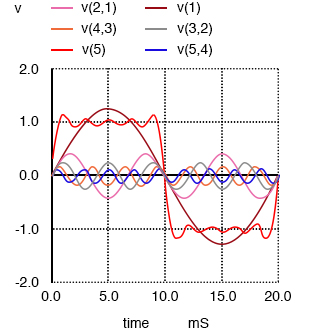
Конечный результат сложения первых пяти нечетных гармонических сигналов (естественно, с правильной амплитудой) является близким приближением к прямоугольному сигналу. Смысл этого в том, чтобы проиллюстрировать, как мы можем построить прямоугольный сигнал из множества синусоидальных сигналов с разными частотами, чтобы доказать, что чистый прямоугольный сигнал фактически эквивалентен последовательности синусоидальных сигналов. Когда напряжение прямоугольного сигнала подается на цепь с реактивными компонентами (конденсаторами и катушками индуктивности), эти компоненты реагируют так, как если бы они подвергались воздействию нескольких синусоидальных напряжений с разными частотами, что фактически так и есть.

Тот факт, что повторяющиеся несинусоидальные сигналы эквивалентны определенной сумме комбинации постоянного напряжения, синусоидальных сигналов и/или косинусоидальных сигналов, является следствием того, как работают волны: фундаментальное свойство всех связанных с волнами явлений, электрических или иных. Математический процесс разбора несинусоидальной волны на составляющие частоты называется анализом Фурье, детали которого выходят далеко за рамки этого текста. Тем не менее, были созданы компьютерные алгоритмы для выполнения этого анализа на высоких скоростях на реальных сигналах, и его применение для анализа сигналов широко распространено.

SPICE имеет возможность выборки формы волны и преобразования ее в составляющие ее синусоидальные гармоники с помощью алгоритма преобразования Фурье с выводом частотного анализа в виде таблицы значений. Давайте попробуем это на прямоугольной волне, которая, как мы уже знаем, состоит из нечетных синусоидальных гармоник:

squarewave analysis netlist
 v1 1 0 pulse (-1 1 0 .1m .1m 10m 20m) 
 r1 1 0 10k 
 .tran 1m 40m 
 .plot tran v(1,0) 
 .four 50 v(1,0) 
 .end

Опция pulse в строке списка соединений, описывающей источник напряжения v1, инструктирует SPICE моделировать «импульсный» сигнал прямоугольной формы, в данном случае симметричный (равное время для каждого полупериода) и имеющий пиковую амплитуду 1 вольт. Сначала мы построим прямоугольный сигнал, который будем анализировать:

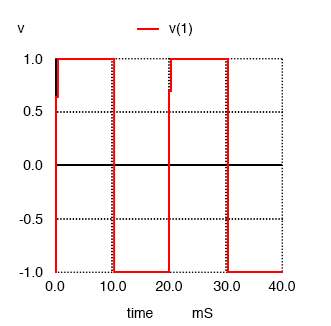
Далее мы распечатаем результаты анализа Фурье, сгенерированные SPICE для этой прямоугольной волны:

fourier components of transient response v(1)    
dc component =  -2.439E-02
harmonic  frequency   fourier     normalized   phase   normalized
no          (hz)     component    component    (deg)   phase (deg)
1         5.000E+01   1.274E+00     1.000000    -2.195       0.000
2         1.000E+02   4.892E-02     0.038415   -94.390     -92.195
3         1.500E+02   4.253E-01     0.333987    -6.585      -4.390
4         2.000E+02   4.936E-02     0.038757   -98.780     -96.585
5         2.500E+02   2.562E-01     0.201179   -10.976      -8.780
6         3.000E+02   5.010E-02     0.039337  -103.171    -100.976
7         3.500E+02   1.841E-01     0.144549   -15.366     -13.171
8         4.000E+02   5.116E-02     0.040175  -107.561    -105.366
9         4.500E+02   1.443E-01     0.113316   -19.756     -17.561
total harmonic distortion =     43.805747  percent

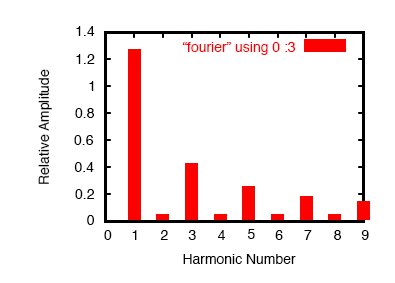
Здесь (рисунок выше) SPICE разбил форму волны на спектр из синусоидальных частот вплоть до девятой гармоники плюс небольшое постоянное напряжение, отмеченное как dc component. Я должен был сообщить SPICE основную частоту (для прямоугольной волны с периодом 20 миллисекунд эта частота равна 50 Гц), чтобы он знал, как классифицировать гармоники. Обратите внимание, насколько малы амплитуды всех четных гармоник (2-й, 4-й, 6-й, 8-й) и как уменьшаются амплитуды нечетных гармоник (1-я самая большая, 9-я самая маленькая).

Этот же метод «преобразования Фурье» часто используется в компьютеризированных системах для выборки сигнала переменного тока и определения его гармонических составляющих. Распространенным компьютерным алгоритмом (последовательность шагов программы для выполнения задачи) для этого является быстрое преобразование Фурье или функция БПФ (FFT, Fast Fourier Transform). Вам не нужно беспокоиться о том, как именно работают эти компьютерные процедуры, но нужно знать об их существовании и применении.

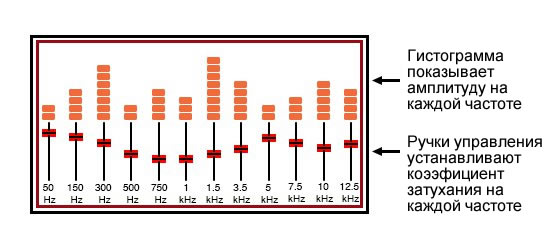
Та же математическая техника, используемая в SPICE для анализа гармонических составляющих сигналов, может быть применена к техническому анализу музыки: разбивку любого конкретного звука на составляющие его частоты синусоид. На самом деле, вы, возможно, уже видели устройство, предназначенное для этого. Графический эквалайзер - это оборудование, которое управляет (а иногда и отображает) характером гармонического состава музыки. Оснащенный несколькими регуляторами или ползунками, эквалайзер способен избирательно ослаблять (уменьшать) амплитуду определенных частот, присутствующих в музыке, чтобы «настраивать» звук для удобства слушателя. Как правило, рядом с каждым рычагом управления будет отображаться «гистограмма», отображающая амплитуду на каждой конкретной частоте.

Устройство, построенное только для отображения (не для управления) амплитуд каждого частотного диапазона сигнала смешанных частот, обычно называется анализатором спектра. Конструкция анализаторов спектра может быть как простой, как набор «фильтрующих» схем (подробности смотрите в следующей главе), предназначенных для разделения различных частот друг от друга, так и сложной, как специализированный компьютер, использующий алгоритм БПФ для математического разделения сигнала на его гармонические составляющие. Анализаторы спектра часто предназначены для анализа высокочастотных сигналов, например сигналов радиопередатчиков и компьютерного сетевого оборудования. В таком виде они часто выглядят как осциллограф:

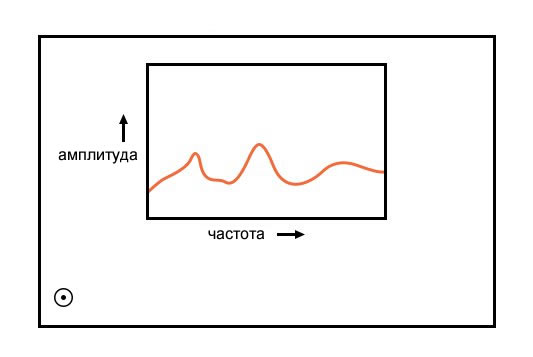
Как и осциллограф, анализатор спектра использует дисплей для отображения графика сигнала. В отличие от осциллографа, этот график представляет собой зависимость амплитуды от частоты, а не амплитуды от времени. По сути, анализатор показывает график амплитудно-частотной характеристики сигнала: то, что инженер мог бы назвать анализом в частотной области, а не анализом во временной области.

Термин «область» является математическим: усложненный вариант для описания горизонтальной оси графика. Таким образом, график осциллографа – амплитуды (по вертикали) во времени (по горизонтали) – является анализом во «временной области», тогда как график анализатора – спектра амплитуды (по вертикали) по частоте (по горизонтали) – является анализом в «частотной области». Когда мы используем SPICE для построения графика амплитуды сигнала (амплитуды напряжения или тока) в диапазоне частот, мы выполняем анализ в частотной области.

Обратите внимание на то, что анализ Фурье из последнего моделирования SPICE не является «идеальным». В идеале, амплитуды всех четных гармоник должны быть абсолютно равны нулю, как и постоянная составляющая. Опять же, это не столько причуда SPICE, сколько свойство волн в целом. Волна бесконечной продолжительности (бесконечное число циклов) может быть проанализирована с абсолютной точностью, но чем меньше циклов доступно для анализа, тем менее точен анализ. Анализ Фурье может свести форму сигнала к определенному ряду синусоидальных сигналов, только когда у нас есть уравнение, описывающее сигнал в целом. Чем меньше циклов сигнала, тем меньше его частота. Если довести эту концепцию до логического предела, короткий импульс – сигнал, который даже не завершает цикл, – фактически не имеет частоты, а скорее действует как бесконечный диапазон частот. Этот принцип является общим для всех волновых явлений, а не только для переменных напряжений и токов.

Достаточно сказать, что число циклов и достоверность частотного компонента (-ов) сигнала связаны напрямую. Мы могли бы улучшить точность нашего анализа, позволив колебаниям сигнала пройти много циклов, и в результате был бы спектральный анализ, более соответствующий идеалу. В следующем анализе для краткости я опустил график формы сигнала – это просто очень длинный прямоугольный сигнал:

square wave 
v1 1 0 pulse (-1 1 0 .1m .1m 10m 20m)   
r1 1 0 10k      
.option limpts=1001     
.tran 1m 1      
.plot tran v(1,0)       
.four 50 v(1,0) 
.end  
fourier components of transient response v(1)    
dc component =   9.999E-03
harmonic  frequency    fourier    normalized   phase   normalized
no           (hz)     component   component    (deg)   phase (deg)
1         5.000E+01   1.273E+00     1.000000    -1.800       0.000
2         1.000E+02   1.999E-02     0.015704    86.382      88.182
3         1.500E+02   4.238E-01     0.332897    -5.400      -3.600
4         2.000E+02   1.997E-02     0.015688    82.764      84.564
5         2.500E+02   2.536E-01     0.199215    -9.000      -7.200
6         3.000E+02   1.994E-02     0.015663    79.146      80.946
7         3.500E+02   1.804E-01     0.141737   -12.600     -10.800
8         4.000E+02   1.989E-02     0.015627    75.529      77.329
9         4.500E+02   1.396E-01     0.109662   -16.199     -14.399

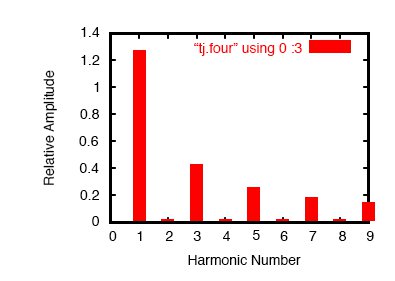
Обратите внимание, что этот анализ (рисунок выше) показывает меньшее напряжение компонента постоянного напряжения и более низкие амплитуды для каждого синусоидального сигнала четных гармоник, и все это потому, что мы позволяем компьютеру сделать выборку большего количества циклов сигнала. Опять же, неточность первого анализа – не столько недостаток SPICE, сколько фундаментальное свойство волн и анализа сигналов.

Резюме

• Прямоугольные сигналы эквивалентны синусоиде на той же (основной) частоте, добавленной к бесконечному ряду нечетно-кратных синусоидальных гармоник с уменьшающимися амплитудами.
• Существуют компьютерные алгоритмы, которые способны делать выборку формы сигналов и определять составляющие их синусоидальные компоненты. Алгоритм преобразования Фурье (в частности, быстрое преобразование Фурье, или БПФ, FFT) обычно используется в программах компьютерного моделирования схем, таких как SPICE, и в электронном измерительном оборудовании для определения характеристик сигналов.

Теги