Что такое функция sinc, и почему она важна в электротехнике?
Данная статья на этот частый технический вопрос дает краткий обзор математической функции, которая часто встречается в цифровой обработке сигналов.
Функция sinc и ее нормализованный вариант
Математическая формулировка функции sinc, также известной как функция кардинального синуса, записывается следующим образом:
\[\text{sinc}(x)=\frac{\sin(x)}{x}\]
Показанная выше функция не определена при x = 0, и, следовательно, нам нужно определить sinc(0) на основе предела, когда x стремится к 0, что равно 1. Таким образом,
\[\text{sinc}(x)=\begin{cases}1 & \text{при } x = 0\\\frac{\sin(x)}{x} & \text{при } x \neq 0\ \end{cases}\]
В контексте цифровой обработки сигналов мы часто используем альтернативную форму, в которой независимая переменная умножается на π:
\[\text{sinc}_\pi (x)\equiv\text{sinc}(\pi x)=\begin{cases}1 & \text{при } x = 0\\\frac{\sin(\pi x)}{\pi x} & \text{при } x \neq 0 \end{cases}\]
Эта вторая форма называется нормированной функцией sinc, потому что определенный интеграл данной функции по всему диапазону x равен 1:
\[\int_{-\infty}^{\infty}\text{sinc}_\pi(x)dx=1\]
Я упоминал, что нормированная версия широко используется при цифровой обработке сигналов. Когда вместо переменной, непрерывной по времени, мы имеем дело с дискретными данными, нормирование выражается следующим образом:
\[\sum_{n=-\infty}^{\infty}\text{sinc}_\pi[n]=1\]
Следующий график показывает форму функции sinc, а также передает разницу, возникающую при умножении независимой переменной на π.
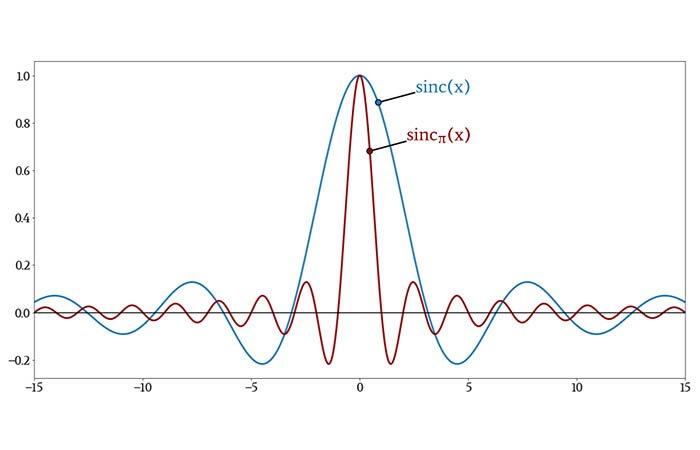
Функция sinc в обработке сигналов
Результат преобразования Фурье функции sinc представляет собой прямоугольник с центром в точке ω = 0. Это позволяет sinc(x) занимать особое место в области обработки сигналов, потому что прямоугольная форма в частотной области является идеализированным откликом идеального фильтра, называемого в англоязычной литературе «brick-wall filter» (фильтр «кирпичная стена»). Другими словами, sinc(x) – это импульсная характеристика идеального фильтра нижних частот.
Использование функции sinc в приложениях фильтрации более заметно в области цифровой обработки сигналов. Следующая диаграмма иллюстрирует сходство между импульсной характеристикой КИХ-фильтра и графиком sinc(x).
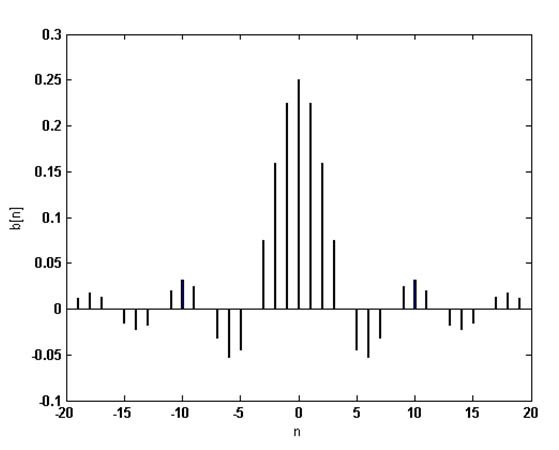
Преобразование Фурье функции sinc представляет собой прямоугольник, а результат преобразования Фурье прямоугольного импульса представляет собой функцию sinc. Если нам нужно сократить дискретный по времени сигнал для выполнения спектрального анализа, мы можем умножить его на прямоугольное окно, и эта операция эквивалентна свертке преобразования Фурье сигнала с функцией sinc.
Функция sinc также появляется при анализе цифро-аналогового преобразования. Идеализированное восстановление аналогового сигнала представляет собой последовательность импульсов, но реальные ЦАП создают «ступенчатую» форму сигнала, применяя к выходным отсчетам удержание нулевого порядка. В частотной области удержание нулевого порядка приводит к выходному спектру, который соответствует идеализированному спектру, умноженному на функцию sinc.
