Схемы делителей тока

Добавлено 15 января 2021 в 04:50

Параллельную цепь часто называют делителем тока из-за ее способности делить общий ток на дробные части.

Чтобы понять, что это означает, давайте сначала проанализируем простую параллельную цепь, определив токи ветвей через отдельные резисторы.

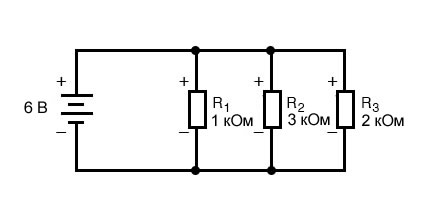
Рисунок 1 Простая параллельная схема — Рисунок 1 – Простая параллельная схема

Зная, что напряжения на всех компонентах в параллельной цепи одинаковы, мы можем заполнить верхнюю строку нашей таблицы напряжение/ток/ сопротивление значением 6 вольт:

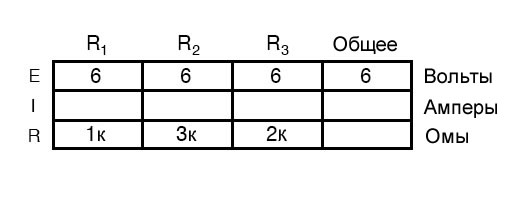
Рисунок 2 Табличный метод. Шаг 1 — Рисунок 2 – Табличный метод. Шаг 1

Используя закон Ома (I = E/R), мы можем рассчитать ток каждой ветви:

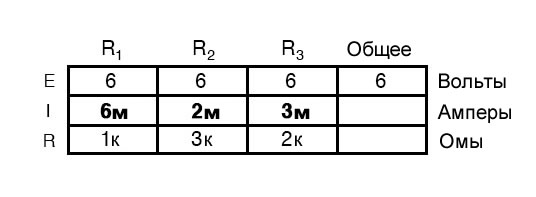
Рисунок 3 Табличный метод. Шаг 2 — Рисунок 3 – Табличный метод. Шаг 2

Зная, что токи ветвей в параллельных цепях складываются, чтобы равняться общему току, мы можем получить общий ток, суммируя 6 мА, 2 мА и 3 мА:

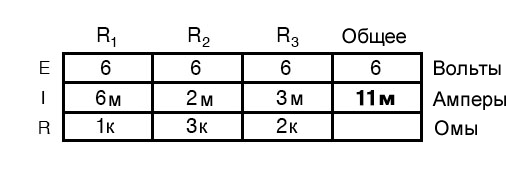
Рисунок 4 Табличный метод. Шаг 3 — Рисунок 4 – Табличный метод. Шаг 3

Последний шаг, конечно же, – это подсчитать общее сопротивление. Это можно сделать с помощью закона Ома (R = E/I) в столбце «общее» или с помощью формулы сопротивления из отдельных параллельных сопротивлений. В любом случае мы получим один и тот же ответ:

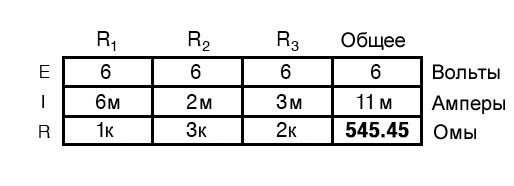
Рисунок 5 Табличный метод. Шаг 4 — Рисунок 5 – Табличный метод. Шаг 4

И снова должно быть очевидно, что ток через каждый резистор связан с его сопротивлением, учитывая, что напряжение на всех резисторах одинаково. Здесь соотношение не прямо пропорционально, а, наоборот, обратно пропорционально. Например, ток через R₁ в два раза больше, чем ток через R₃, который имеет в два раза большее сопротивление, чем R₁.

Если бы мы изменили напряжение питания этой схемы, мы обнаружили бы, что (сюрприз!) эти пропорции не меняются:

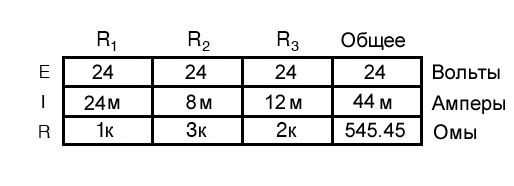
Рисунок 6 Сохранений пропорций между сопротивлениями и токами — Рисунок 6 – Сохранений пропорций между сопротивлениями и токами

Расчет коэффициентов отношений токов

Ток через R₁ по-прежнему ровно вдвое больше, чем у R₃, несмотря на то, что напряжение источника изменилось. Пропорциональность между токами разных ветвей строго зависит от сопротивлений.

О делителях напряжения напоминает тот факт, что токи ветвей представляют собой фиксированные доли общего тока. Несмотря на четырехкратное увеличение напряжения питания, соотношение между током любой ветви и полным током остается неизменным:

\[\frac{I_{R1}}{I_{общ}} = \frac{6 \ мА}{11 \ мА} = \frac{24 \ мА}{44 \ мА} = 0,54545\]

\[\frac{I_{R2}}{I_{общ}} = \frac{2 \ мА}{11 \ мА} = \frac{8 \ мА}{44 \ мА} = 0,18182\]

\[\frac{I_{R3}}{I_{общ}} = \frac{3 \ мА}{11 \ мА} = \frac{11 \ мА}{44 \ мА} = 0,27273\]

Теперь мы можем сами убедиться в том, что мы сделали в начале этой статьи: параллельную цепь часто называют делителем тока из-за ее способности делить общий ток на дробные части.

Формула делителя тока

Применив немного алгебры, мы можем вывести формулу для определения тока через параллельный резистор, не учитывая ничего кроме общего тока, отдельного сопротивления и общего сопротивления:

Ток через любой резистор:

\[I_n = \frac{E_n}{R_n}\]

Напряжение в параллельной цепи:

\[E_{общ} = E_n = I_{общ}R_{общ}\]

Подставляем I_общR_общ вместо E_n в первую формулу...

Ток через любой параллельный резистор:

\[I_n = \frac{ I_{общ}R_{общ}}{R_n}\]

или

\[\large I_n = I_{общ} \frac{ R_{общ}}{R_n}\]

Отношение полного сопротивления к отдельному сопротивлению равно отношению отдельного тока (ветви) к общему току. Эта формула известно как формула делителя тока и является сокращенным методом определения токов ветвей в параллельной цепи, когда известен полный ток.

Пример формулы делителя тока

Используя исходную параллельную схему в качестве примера, мы можем по этой формуле пересчитать токи ветвей, если мы начнем, зная общий ток и общее сопротивление:

\[I_{R1} = 11 \ мА \frac{545,45 \ Ом}{1 \ кОм} = 6 \ мА\]

\[I_{R2} = 11 \ мА \frac{545,45 \ Ом}{3 \ кОм} = 2 \ мА\]

\[I_{R3} = 11 \ мА \frac{545,45 \ Ом}{2 \ кОм} = 3 \ мА\]

Если вы потратите время на сравнение формул двух делителей, вы увидите, что они очень похожи. Однако обратите внимание, что отношение в формуле делителя напряжения – это R_n (отдельное сопротивление), деленное на R_общ, а отношение в формуле делителя тока – это R_общ, деленное на R_n:

\[\begin{matrix} \text{делитель напряжения} & \text{делитель тока} \\ E_n = I_{общ} \frac{R_n}{R_{общ}} & I_n = E_{I} \frac{R_{общ}}{R_n} \end{matrix}\]

Формула делителя тока и формула делителя напряжения

Эти две формулы довольно легко спутать, взяв обратные соотношения сопротивлений. Один из способов помочь запомнить правильную форму – это помнить, что оба отношения в формулах делителей напряжения и тока должны быть меньше единицы. В конце концов, это формулы делителей, а не формулы умножителей! Если дробь перевернута, то соотношение будет больше единицы, что неверно.

Зная, что полное сопротивление в последовательной цепи (делитель напряжения) всегда больше, чем любое из отдельных сопротивлений, мы знаем, что дробная часть для этой формулы должна быть R_n над R_общ. И наоборот, зная, что полное сопротивление в параллельной цепи (делитель тока) всегда меньше, чем любое из отдельных сопротивлений, мы знаем, что дробь для этой формулы должна быть R_общ над R_n.

Пример применения схемы делителя тока: электрическая измерительная схема

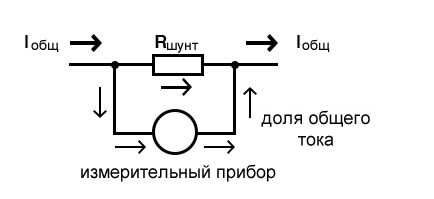
Цепи делителей тока также находят применение в измерительных схемах, где требуется, чтобы часть измеряемого тока проходила через чувствительный прибор. Используя формулу делителя тока, можно подобрать подходящий шунтирующий резистор таким образом, чтобы через измерительный прибор всегда проходила точно заданная доля общего тока:

Рисунок 7 Измерительная схема — Рисунок 7 – Измерительная схема

Резюме

Параллельные цепи делят общий ток цепи между токами отдельных ветвей, причем коэффициенты деления строго зависят от сопротивлений: I_n = I_общ(R_общ/R_n)