Понятие линейно-фазовых фильтров
Линейная фазовая характеристика, также известная как постоянное групповое время задержки, является важным свойством в некоторых применениях фильтров. Рассмотрим понятие линейной фазовой характеристики чуть подробнее.
В большинстве обсуждений фильтров акцент делается на амплитуду. Если нам требуется сглаживание для АЦП, нам нужен фильтр нижних частот, то есть схема, которая поддерживает (или увеличивает) амплитуду низкочастотных сигналов и уменьшает амплитуду высокочастотных сигналов. Если мы удаляем из аудиосигнала смещение по постоянному напряжению, мы используем фильтр верхних частот, но при этом мы должны убедиться, что частота среза достаточно низка, чтобы избежать уменьшения амплитуды сигнала на частотах, которые мы хотим услышать.
Однако важно помнить, что фильтры влияют не только на амплитуду сигнала, но и на его фазу.
Например, простейший RC-фильтр нижних частот вносит в выходной синусоидальный сигнал сдвиг фазы выходной синусоиды до 90° относительно входного синусоидального сигнала. Предлог «до» в предыдущем предложении очень важен – фактический сдвиг фазы зависит от частоты сигнала, проходящего через фильтр, как показано на следующем графике сдвига фазы в зависимости от частоты для RC-фильтра нижних частот с частотой среза 1 кГц.
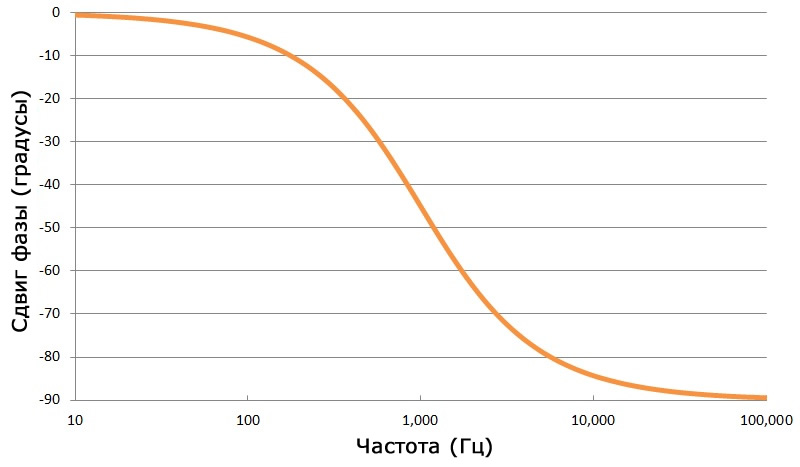
Теперь рассмотрим ситуацию, в которой на фильтр будут подаваться сигналы, состоящие из разных частот, которые работают вместе. Если эти разные частоты испытывают разные задержки, могут возникнуть проблемы. Вот два примера:
- аудио приложения: частоты, представляющие различные высоты тона, чтобы обеспечить правильное воспроизведение звука, должны оставаться синхронизированными;
- цифровая связь: частоты синусоидальных гармонических сигналов, составляющих прямоугольный сигнал, должны испытывать одинаковые задержки, чтобы избежать искажения цифрового сигнала.
На данный момент ситуация может показаться безнадежной – глядя на график выше, мы ясно видим, что фазовый сдвиг резко меняется в зависимости от частоты. Но есть критически важный момент, который меняет всё: мы должны помнить, что в зависимости от частоты изменяется и временной эквивалент, соответствующий конкретному фазовому сдвигу. Рассмотрим следующую диаграмму:
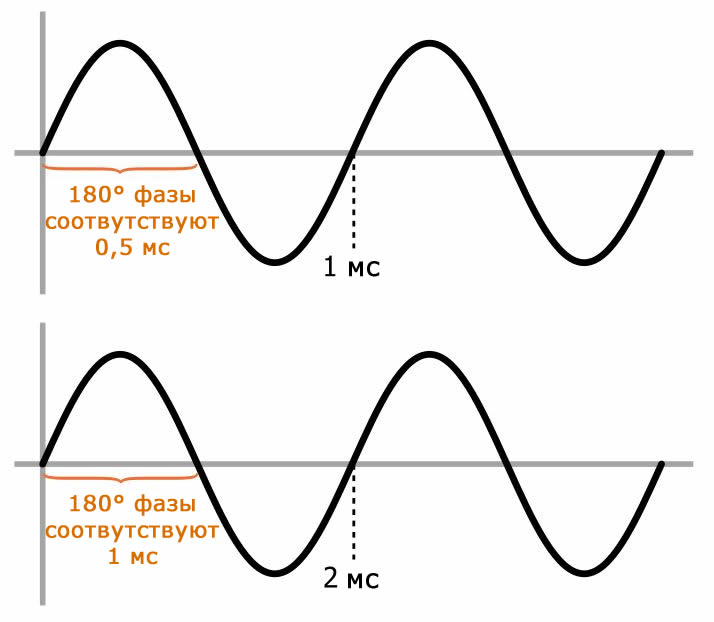
Здесь мы видим два синусоидальных сигнала, один с частотой 1 кГц (то есть период = 1 мс) и один с частотой 500 Гц (то есть период = 2 мс). Конкретный сдвиг фазы (в качестве примера на диаграмме используется 180°) для каждой частоты соответствует разному значению времени: разные частоты соответствуют разным периодам, а сдвиг фазы соответствует определенной части периода.
Из этого следует, что поддержание синхронизации между различными частотными компонентами сигнала не означает принудительного обеспечения одинакового сдвига фазы, поскольку одинаковый сдвиг фазы на разных частотах приведет к различным временным задержкам.
Чтобы добиться равных временных задержек для всех частот, нам нужно, чтобы каждая частота имела свой сдвиг фазы, а именно сдвиг фазы, который приводит на конкретной частоте к задержке, равной задержке на других частотах. Более конкретно, нам нужен сдвиг фазы, который линейно увеличивается по мере увеличения частоты. Это имеет смысл, поскольку при увеличении частоты фиксированный сдвиг фазы соответствует постепенно уменьшающемуся отрезку времени, и, таким образом, для компенсации нам нужен больший сдвиг фазы.
Таким образом, идеальный линейно-фазовый фильтр демонстрирует сдвиг фазы, который линейно увеличивается по мере увеличения частоты, и, таким образом, он обеспечивает постоянную временную задержку (это, главным образом, относится к частотам в полосе пропускания, то есть к частотам, интересующим разработчика). Групповое время задержки пропорционально производной фазо-частотной характеристики по частоте. Производная линейной функции является константой, что объясняет, почему линейная фазо-частотная характеристика также соответствует постоянному групповому времени задержки. Хорошо известной топологией схем, оптимизированной для получения линейного фазового отклика, является фильтр Бесселя.
