Доходность облигаций на все случаи жизни
Проблема расчета той или иной доходности облигации часто заставляет задуматься неискушенного в математических расчетах инвестора. В этом материале мы собрали наиболее популярные виды доходности облигаций и те формулы, которыми можно их определить.

Купонная доходность
По сути это просто величина купона. Если купон по облигации составляет 7%, то и купонная доходность будет аналогичная.
Если перед вами стоит задача вычислить купонную доходность по данным из QUIK, то можно воспользоваться следующей формулой:
\[Coupon \ Yield = { размер \ купона \times \frac{365}{длительность \ купона} \over номинал } = { годовой \ купон \over номинал }\]
Примечание: Здесь и далее полученный результат должен быть приведен к процентному виду путем умножения на 100%. Для простоты восприятия этот шаг был исключен из формул.
Текущая доходность
Текущая доходность обозначает отношение начисляемого купона к актуальной рыночной цене облигации. Она может использоваться в случаях, когда вложения рассматриваются на короткий промежуток времени. В этой ситуации изменением рыночной цены иногда можно пренебречь. Формула следующая:
\[Current \ Yield = { годовой \ купон \over цена \times номинал } = { годовой \ купон \over рыночная \ цена } \]
В данной формуле под «ценой» имеется в виду процентное значение цены, а под «рыночной ценой» — абсолютное, в денежных единицах.
Модифицированная текущая доходность
Этот показатель представляет из себя отношение годового купона к «грязной» цене облигации, включающей НКД. Этот вид доходности может использоваться в случае краткосрочных вложений, когда горизонт инвестиций находится в пределах одного купонного периода. Формула расчета:
\[MCY = { годовой \ купон \over рыночная \ цена \ + \ нкд } = { годовой \ купон \over «грязная» \ цена }\]
«Грязная» цена облигации — это общая цена покупки с учетом уплаченного НКД. Цена без НКД еще иногда называется «чистая» цена.
Если данную доходность разделить на число дней в году (365 или 366) и умножить на число дней, которое инвестор планирует удерживать облигацию, то можно получить ожидаемый процент прибыли от инвестиции. На примере ОФЗ 25083: грязная цена = 997,78 руб., годовой купон 70 руб. (7%). Удерживать будем 35 дней.
\[\frac{70}{997,78} \times 100\% \times \frac{35}{365} = 7,02\% \times 0,0959 = 0,67\%\]
Так как облигация торгуется ниже номинала, то MCY (7,02%) получилась больше купонной доходности. А доход инвестора за 35 дней, при условии сохранения рыночной цены, составит 0,67%.
Простая доходность к погашению
Простая доходность к погашению (иногда называют «простая доходность») учитывает, как купонный доход, так и прибыль/убыток из-за разницы между ценой приобретения и ценой погашения.
\[Yield = {номинал - рыночная \ цена + (все \ будущие \ купоны - НКД) \over рыночная \ цена} \times \frac{365}{дней \ до \ погашения }\]
Пример: возьмем выпуск ОФЗ 25083.

Сегодня 01.03.2019, до погашения остается 1020 дней, которые можно быстро рассчитать в excel, вычитая текущую дату из даты погашения. За этот период держатель получит 6 купонов размером 34,9 руб., в сумме 34,9*6 = 209,4 руб. Расчет простой доходности будет выглядеть следующим образом:
\[Yield = {1000 - (98,34 \times 1000) + (209,4-14,38) \over 98,34 \times 1000} \times \frac{365}{1020} \times 100\%= \frac{211,62}{983,4} \times 35,78\% = 7,7\%\]
Данная формула может применяться в том случае, когда инвестор планирует все получаемые платежи по облигации выводить и тратить на собственные нужды. Также она может быть полезна, если инвестор хочет примерно рассчитать размер налогов, которые придется уплатить с дохода. Для некоторых облигаций налог с купонного дохода и налог с разницы между ценой покупки и погашения различается. Чтобы учесть это различие, можно умножить сумму соответствующего дохода на коэффициент (1-налоговая ставка).
Примечание: формула подходит для обыкновенных купонных облигаций, а также может применяться по отношению к бумагам с переменным купоном, где процентная ставка купона зафиксирована только до даты оферты. В таком случае, доходность также следует рассчитывать не к дате погашения, а к дате оферты. Для флоатеров линкеров и других бумаг с плавающей доходностью данная формула не подходит.
Эффективная доходность к погашению
Самая популярная и самая достоверная оценка доходности облигации. Часто можно ее встретить под аббревиатурой YTM (Yield to Maturity).
По сравнению с предыдущей формулой, она учитывает реинвестирование купонов под ту же доходность на всем сроке владения облигацией. Также она позволяет адекватно учесть выгоду для инвестора от амортизации долга до погашения. Ее значение определяется путем решения следующего уравнения:
\[P = \sum^n_{t=1}\frac{C}{(1+r)^t} + \frac{F}{(1+r)^n}\]
Здесь:
- r — искомая доходность;
- P — текущая «грязная» цена облигации;
- C — получаемый платеж по облигации (купон или купон+амортизация);
- F — финальный платеж (номинал или невыплаченный остаток номинала, в случае амортизации);
- t — число периодов дисконтирования до получения платежа С;
- n — число периодов дисконтирования до получения финального платежа.
Разумеется, вручную проводить такие расчеты достаточно накладно. Но это обычно и ни к чему, так как этот параметр есть в терминале QUIK.
Тем не менее, иногда может понадобиться провести собственные расчеты. Для этого приведем пример, как можно сделать это с использованием Excel.
По умолчанию для таких целей в Excel есть специальная функция ДОХОД(), а также обратная ей функция ЦЕНА(), которая по заданной доходности ищет рыночную цену. Функции имеют следующий синтаксис:
ДОХОД (дата покупки; дата погашения; ставка купона; «грязная цена»; цена погашения; частота выплаты купона; базис)
ЦЕНА (дата покупки; дата погашения; ставка купона; доходность; цена погашения; частота выплаты купона; базис)
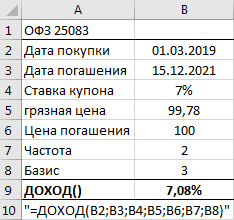
К сожалению, функции ДОХОД() и ЦЕНА() очень часто дают существенную погрешность, как в случае, приведенном на картинке (доходность к погашению в QUIK равна 7,81%). Поэтому можно предложить другой способ расчета, более трудоемкий, но более точный.
Для примера возьмем все ту же ОФЗ 25083. Для начала строим в Excel таблицу всех платежей по облигации, которые будут получены держателем начиная с момента покупки. В дату погашения не забудьте прибавить к купону размер номинала. В начале необходимо добавить дату покупки, под которой будет указана «грязная» цена облигации со знаком «минус». Далее используем функцию ЧИСТВНДОХ() следующим образом:

В данном примере получился результат 7,79%, что отличается от доходности в QUIK 7,81%, но уже гораздо ближе к действительности. Это построение может быть использовано в качестве своего карманного калькулятора доходности, а также может помочь в моделировании доходности по бумагам с плавающим купоном.
Также можно использовать функцию ЧИСТНЗ(), которая позволяет аналогичным образом по заданной доходности и потоку платежей определить рыночную цену. В ячейке B2 в таком случае должно быть нулевое значение, а первым аргументом в функции нужно добавить ставку доходности
Это может помочь при оценке чувствительности облигации к изменению процентных ставок на рынке, а также оценке стоимости продажи облигации в будущем, если инвестор не планирует держать бумагу до погашения.
Примечание: при использовании функций ЧИСТВНДОХ() и ЧИСТНЗ() не стоит слишком округлять числа. Чем больше знаков после запятой будет указано на входе, тем более точный результат получится на выходе. Можно для наглядности выбирать формат отображения с округлением, но в ячейке должно храниться максимально точное значение.
