Простой метод измерения ESR конденсаторов
Точное моделирование электронных схем, в том числе и силовых электронных преобразователей, должно учитывать последовательные сопротивления конденсаторов и катушек индуктивности. Рассмотрим, простой метод, который позволяет измерять эквивалентное последовательное сопротивление конденсатора (ESR).
Конденсаторы классифицируются по типу диэлектрика. Электролитические конденсаторы популярны в силовых электронных схемах благодаря их высокой эффективности относительно размеров и превосходному соотношению цены и качества [1]. К сожалению, с изменением рабочей частоты изменяются и их характеристики, тогда как сопротивление идеального конденсатора с ростом частоты должно уменьшаться. Но в реальном мире это не встречается. Увеличение частоты до определенной точки приводит к ожидаемому уменьшению полного сопротивления, но дальнейшее увеличение частоты вызывает увеличение импеданса, то есть конденсатор действует как резонансная схема. Для моделирования поведения реального конденсатора требуется к модели идеального конденсатора добавить дополнительные элементы. ESR – это фактически сопротивление, которое реальный конденсатор демонстрирует на границе между «поведением конденсатора» и «поведением индуктивности», то есть сопротивление на резонансной частоте.
ESR является важным параметром при моделировании динамического поведения силовых преобразователей, поскольку он предсказывает пульсации выходного сигнала преобразователя, а также предсказывает срок службы конденсатора [2]. Мощность, рассеиваемая в ESR, вызывает повышение температуры конденсатора и уменьшение его емкости и срока службы.
Простой и прямой метод измерения ESR предложен в [3], в котором ESR определяется непосредственно отношением напряжения пульсаций на конденсаторе к току пульсаций. Но реализация довольно дорогая и хлопотная. Чтобы определить ESR, используя только измерения напряжения, Чен и другие [4] предположили, что в некоторых конкретных условиях ток пульсаций индуктивности можно считать постоянным, и, следовательно, выходное напряжение пульсации определяет ESR. Однако предлагаемый способ имеет ограничения и его точность невелика.
Лабораторный метод, который можно использовать для определения величины ESR электролитических конденсаторов, был предложен в [5]. Однако способ слишком дорогостоящий для реализации.
Здесь мы представляем простой метод измерения для определения ESR конденсатора.
Предлагаемый метод
Предположим, что модель, показанная на рисунке 1, представляет собой тестируемый конденсатор (CUT, Capacitor Under Test):
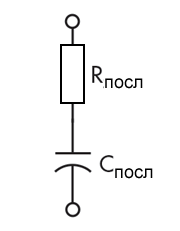
Эта модель игнорирует индуктивность выводов. Предположим, что, как показано на рисунке 2, тестируемый конденсатор подключен к генератору синусоидального сигнала с частотой Fг, внутреннее сопротивление генератора равно rг:
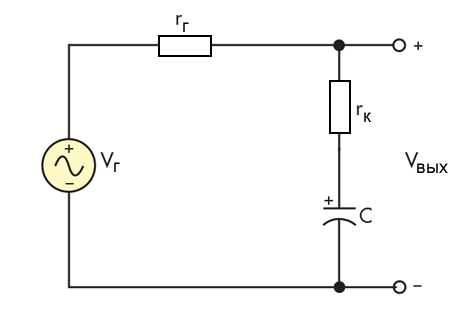
Передаточная функция этой схемы:
\[H(s) = {r_к \over r_к + r_г} \times { s + \frac{1}{r_к \times C} \over s + \frac{1}{(r_к + r_г) \times C} } \qquad (1)\]
Уравнение 1 показывает высокочастотный характер этой цепи. Поэтому мы можем аппроксимировать передаточную функцию как:
\[H(s) = {r_к \over r_к + r_г} \cong {r_к \over r_г} \qquad (2)\]
Уравнение 2 является основой для нашего измерения ESR конденсатора. Когда входная частота достаточно высока, мы можем упростить отношение входного и выходного напряжений до алгебраического уравнения 2. Для высоких частот схема действует как аттенюатор с коэффициентом ослабления:
\[\alpha = {r_к \over r_к + r_г} \qquad\]
Измерение коэффициента затухания цепи и внутреннего сопротивления генератора приводит к rк, то есть эквивалентному последовательному сопротивлению (ESR) конденсатора:
\[r_к = \alpha \times r_г \qquad (3)\]
Вместо использования синусоидального возбуждения мы можем использовать прямоугольный сигнал. Это позволяет нам использовать ряд Фурье для записи уравнения с уровнями + Vm и -Vm и периодом T:
\[\sum_{n=1,3,5,...}^{\infty} {4 \times V_m \over n \times \pi} \sin(n \times \omega_0 \times t) \qquad (4)\]
где:
\[\omega_0 = \frac{2\pi}{T} = \text{угловая частота прямоугольного сигнала}\]
Прямоугольный сигнал состоит из нечетных гармоник. Когда основная гармоника достаточно высока, конденсатор действует как короткое замыкание, а выходное напряжение примерно является ослабленной версией входного напряжения в устойчивом состоянии. Затухание цепи в установившемся режиме напрямую связано с эквивалентным последовательным сопротивлением конденсатора, rк, которое может быть получено путем измерения коэффициента затухания цепи и использования уравнения 3.
Результаты моделирования
Диаграмма Simulink показана на рисунке 3:
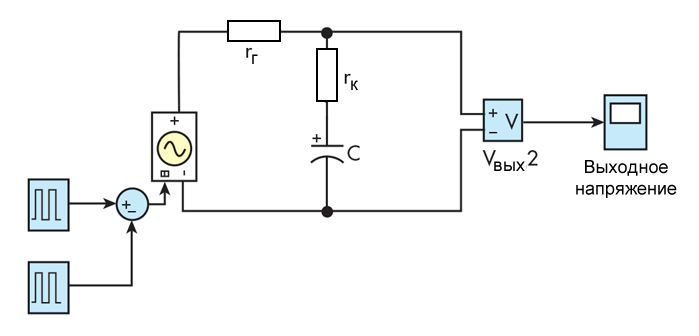
В качестве возбуждения используется прямоугольный сигнал с амплитудой +1 и -1 вольт. Выходное сопротивление генератора сигналов принимается за 50 Ом, конденсатор составляет 30 мкФ с ESR 0,8 Ом. Установившаяся форма выходного сигнала показана на рисунке 4:
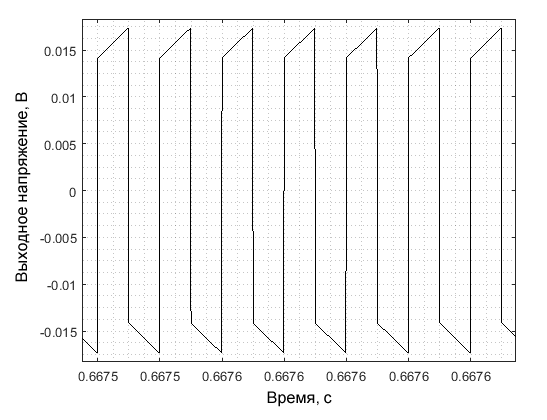
Расчетный коэффициент затухания цепи составляет:
\[\alpha = { \text{выходное напряжение пик-пик} \over \text{входное напряжение пик-пик} } = \frac{0,315}{2} = 0,0158 \qquad (5)\]
и ESR тестируемого конденсатора рассчитывается как:
\[r_к = \alpha \times r_г = 0,0158 \times 50 = 0,7875\ Ом \qquad (5)\]
Лабораторные результаты
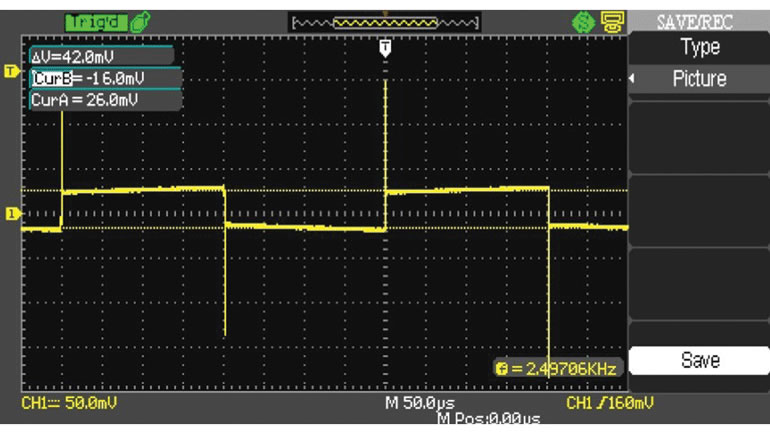
Возбуждение обеспечивает генератор сигналов с номинальным выходным сопротивлением 50 Ом. С помощью простого делителя напряжения намеряется выходное сопротивление 47,1 Ом. Выходное напряжение пик-пик в установившемся состоянии измеряется с помощью цифрового осциллографа. На рисунке 5 показан пример выходного напряжения.
Расчетные значения ESR
| Размах входного напряжения, В | Размах выходного напряжения, мВ | Емкость, мкФ | Рассчитанное значение ESR, Ом |
|---|---|---|---|
| 1,68 | 58 | 4 | 1,68 |
| 1,68 | 80 | 6,8 | 2,35 |
| 1,68 | 66 | 47 | 1,88 |
| 1,72 | 44,8 | 220 | 1,26 |
| 1,72 | 48 | 470 | 1,35 |
| 1,68 | 42 | 660 | 1,18 |
| 1,72 | 45 | 2200 | 1,26 |
Этот простой метод измерения обеспечивает точные результаты и позволяет получить более точную модель силового преобразователя.
Ссылки
- Amaral A.M.R., Cardoso A.J.M.: An experimental technique for estimating the ESR and reactance intrinsic values of aluminium electrolytic capacitors. Proc. Instrumentation and Measurement Technology Conf., IMTC 2006, April 2006, pp. 1820–1825.
- Sankaran V.A., Rees F.L., Avant C.S.: Electrolytic capacitor life testing and prediction. Proc. 32nd Annual Meeting IEEE Industry Applications Society, October 1997, vol. 2, pp. 1058–1065
- Venet P., Perisse F., El-Husseini M.H., Rojat G.: Realization of a smart electrolytic capacitor circuit, IEEE Ind. Appl. Mag., 2002, 8, (1), pp. 16–20
- Chen Y.-M., Chou M.-W., Wu H.-C.: Electrolytic capacitor failure prediction of LC filter for switching-mode power converters. Proc. 40th Annual Meeting IEEE Industry Applications Society, October 2005, vol. 2, pp. 1464–1469.
- Amaral A.M.R., Cardoso A.J.M.: An ESR meter for high frequencies. Proc. Int. Conf. on Power Electronics and Drives Systems, PEDS, 2005, pp. 1628–163
- D.W. Hart, "Power electronics," Mc Graw Hill, 2010.
- N. Mohan,T. M. Undeland , W. P. Robbins, "Power Electronics: Converters, Applications and Design," John Wiley and Sons, 2002.
- R.W. Ericson, D. Maksimovic, "Fundamental of power electronics," Springer, 2001.
- A.M.R. Amaral, A.J.M Cardoso: "An ESR meter for high frequencies". Proc. Int. Conf. on Power Electronics and Drives Systems, PEDS, 2005, pp. 1628–1633.
- R. Chen, J.D.V. Wyk, S. Wang, W.G. Odendaal: Improving the characteristics of integrated EMI filters by embedded conductive layers. IEEE Trans. Power Electron., 2005, pp. 611–619.
- A.M.R. Amaral, A.J.M Cardoso: An experimental technique for estimating the ESR and reactance intrinsic values of aluminium electrolytic capacitors. Proc. Instrumentation and Measurement Technology Conf., IMTC 2006, April 2006, pp. 1820–1825.
