Циклический избыточный код (CRC): обнаружение (и даже исправление) ошибок в цифровых данных
В данной статье кратко объясняется, что такое CRC, и как вы можете использовать его, чтобы сделать вашу цифровую связь более надежной.
Мир сейчас полностью зависит от хранения и передачи цифровых данных. Самолеты, фондовые рынки, системы безопасности, скороварки – современная жизнь быстро обрушится в хаос, если мы не сможем обеспечить точность в постоянно текущем и необъятно огромном потоке из единиц и нулей.
Есть две основные задачи, связанные с поддержанием целостности наших цифровых данных. Первое – это избегать в первую очередь ошибок; эта цель включает в себя множество инженерных практик, которые способствуют надежной передаче и приему цифровых данных. Но, несмотря на все наши усилия, ошибки возможны, и это приводит нас ко второй задаче: обнаружение ошибок. Если система может обнаруживать ошибки, она также может компенсировать эти ошибки, просто отбросив сомнительные данные или запросив повторную передачу.
Выбор метода обнаружения ошибок
Если вы знакомы с битом четности, который иногда используется в связи через UART, вы что-то знаете об обнаружении ошибок. Но бит четности является довольно жалким механизмом обнаружения ошибок; на самом деле, насколько я могу судить, большинство методов обнаружения ошибок более или менее жалки по сравнению с циклическим избыточным кодом (CRC, cyclic redundancy check), который явно стал доминирующим подходом – некоторые крупные имена в цифровой связи (включая CAN, USB и Ethernet) используют CRC как часть своего протокола передачи данных.
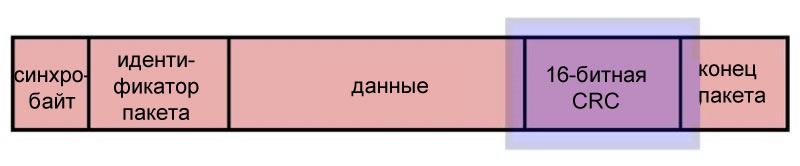
Эффективный, но не простой
Эта короткая статья не является местом для изучения подробностей вычислений и производительности CRC. Суть в том, что двоичный «многочлен» применяется к потоку данных таким образом, чтобы генерировать контрольную сумму, которая, скорее всего, изменится, если один или несколько битов сообщении были изменены.
Этот «многочлен» представляет собой просто математически удобный способ обращения к определенной последовательности битов. Например:
\(x^{16}+x^{12}+x^5+1=0001\ 0000\ 0010\ 0001\)
Это широко используемый полином «CCITT». Это полином 16-го порядка, что означает, что соответствующее двоичное число имеет ширину 16 бит, и что итоговая контрольная сумма CRC будет иметь ширину 16 бит. (Обратите внимание, что коэффициент для члена высшего порядка считается равным 1 и опускается в двоичной версии.) Члены, которые не отображаются в математическом выражении, имеют в качестве коэффициента двоичный 0.
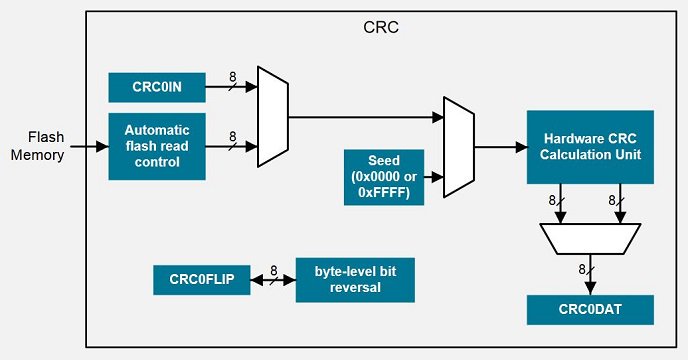
Два CRC, не один
Создание CRC только для исходного сообщения вам не поможет. Ключом к реализации обнаружения ошибок CRC является обеспечение того, чтобы и передатчик, и приемник генерировали контрольную сумму одним и тем же способом.
Передатчик генерирует контрольную сумму для передаваемых данных и включает ее в исходное сообщение, а приемник генерирует собственную контрольную сумму с использованием полученных данных. Если сообщение приемника не совпадает с сообщением передатчика, весьма вероятно, что контрольные суммы будут отличаться; таким образом, приемник считает данные ошибочными, если контрольные суммы CRC не совпадают.
Куда двигаться дальше
Вы должны знать, что обработка CRC может использоваться фактически для исправления ошибок, а не просто для их обнаружения. Здесь мы имеем дело с двоичными данными, поэтому, если CRC позволяет нам идентифицировать ошибочный бит, мы можем восстановить исходную информацию, просто переключив этот бит.
В следующих статьях мы рассмотрим подробности исправления ошибок на базе CRC.
