Математика проектирования I2C: емкость и сопротивление

Добавлено 7 ноября 2018 в 02:39

Рассмотрим шину I²C и некоторые проблемы проектирования, которые с ней приходят, включая пороги логических уровней, факторы, которые могут влиять на емкость, и минимальные и максимальные значения номиналов подтягивающих резисторов.

В данной статье рассматривается, какие переменные влияют на емкость вашей шины. В ней также рассматриваются математические расчеты, используемые для определения номиналов подтягивающих резисторов и определения максимальной длины трасс схемы. Начнем с обсуждения того, что такое I²C.

Связанная информация

О шине I²C

I2C – это последовательный интерфейс, допускающий наличие на шине нескольких ведущих устройств (master) и нескольких ведомых устройств (slave) и позволяющий микрочипам взаимодействовать друг с другом на стандартных скоростях 100 кГц (Standard Mode), 400 кГц (Fast Mode), 1 МГц (Fast Mode Plus) и 3,4 МГц (High-Speed Mode).

Одна из наших предыдущих статей, «Шина I2C. Подробности аппаратной реализации», подробно объясняет механизм работы шины I2C. Спецификацию шины можно найти на сайте NXP.

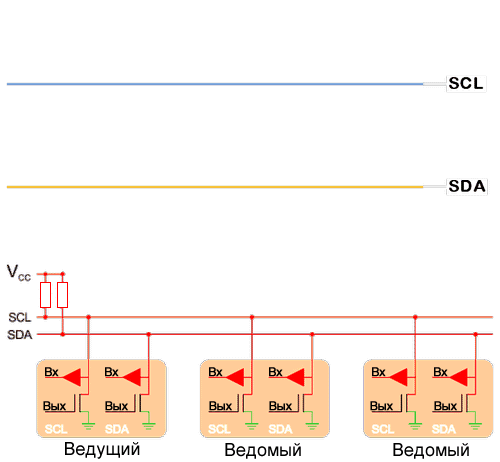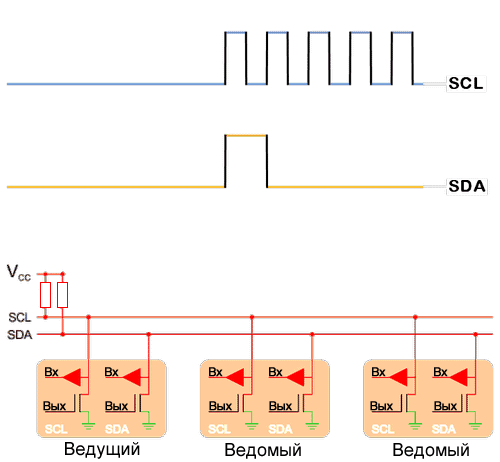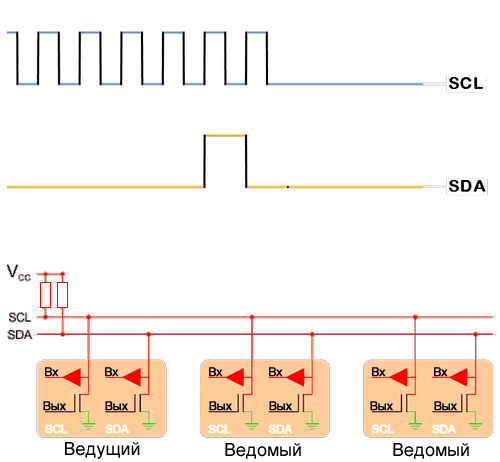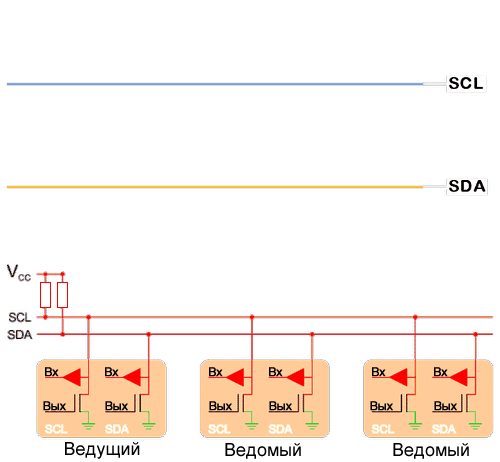
Аппаратная конфигурация I2C и упрощенные формы сигналов (тактового и данных)

Реальные передачи по I2C – это не прямоугольные импульсы, обычно изображаемые на рисунках. Схемы имеют собственный импеданс из-за наличия паразитной емкости и использования подтягивающих резисторов.

Переходы с высокого логического уровня на низкий связаны с током разряда через низкоимпедансный канал NMOS транзистора – эти переходы быстрые. Переходы с низкого логического уровня на высокий включают в себя ток, который должен протекать через относительно большой подтягивающий резистор. Более низкое сопротивление подтягивающих резисторов приводит к более быстрым переходам, но и к более высокому потреблению тока (когда сигнал находится в низком логическом состоянии); более высокое сопротивление подтягивающих резисторов приводит к более медленным переходам и меньшему потреблению тока. Выбор номинала резистора становится более важным на более высоких частотах.

Положительные переходы кажутся скругленными из-за подтягивающих резисторов в пути протекания тока при переходе с низкого логического уровня к высокому логическому уровню

Любое увеличение емкости шины или сопротивления увеличит время перехода к высокому логическому уровню. В какой-то момент разность потенциалов даже не достигнет порога высокого логического уровня, или она не будет оставаться на этом уровне достаточно долго, прежде чем начнется переход обратно к низкому логическому уровню.

На приведенном выше графике постоянная времени RC цепи слишком велика, и напряжение не достигает порога высокого логического уровня

Разные I2C устройства могут иметь разные пороги логических уровней. На предыдущих графиках предполагаются пороги \(V_{лог.низ.} = 0,3 \cdot 3,3В = 1В\) и \(V_{лог.выс.} = 0,7 \cdot 3,3В = 2,3В\), но это не всегда так. Например, ADP5062 имеет пороговые значения \(V_{лог.низ.} = 0,5В\) и \(V_{лог.выс.} = 1,2В\).

На одной и той же шине могут использоваться микросхемы с различными пороговыми напряжениями; когда это происходит, расчеты должны выполняться с использованием наивысшего порогового напряжения высокого логического уровня и наименьшего порогового напряжения низкого логического уровня.

Данный график показывает гипотетическое пороговое напряжение низкого логического уровня 0,7В и гипотетическое пороговое напряжение высокого логического уровня 1,3В. Эти низкие значения увеличивают время, проведенное в состоянии высокого логического уровня, без значительного изменения времени, проведенного в состоянии низкогологического уровня. Данная конфигурация позволяет работать с более высокой частотой. — Данный график показывает гипотетическое пороговое напряжение низкого логического уровня 0,7В и гипотетическое пороговое напряжение высокого логического уровня 1,3В. Эти низкие значения увеличивают время, проведенное в состоянии высокого логического уровня, без значительного изменения времени, проведенного в состоянии низкого логического уровня. Данная конфигурация позволяет работать с более высокой частотой.

Емкость

В спецификации NXP указано, что максимальная общая емкость шины составляет 400 пФ для устройств режимов Standard Mode и Fast Mode и 550 пФ для устройств режима Fast Mode Plus. Вы не должны добавлять конденсаторы на линии I2C, чтобы достичь этих верхних пределов емкости – чем емкость шины меньше, тем лучше.

Диэлектрики

На общую емкость вашей шины может повлиять основной материал вашей печатной платы. Диэлектрическая постоянная для большинства базовых материалов печатных плат находится в диапазоне 2,5≲ε≲5 (ε зависит от частоты).

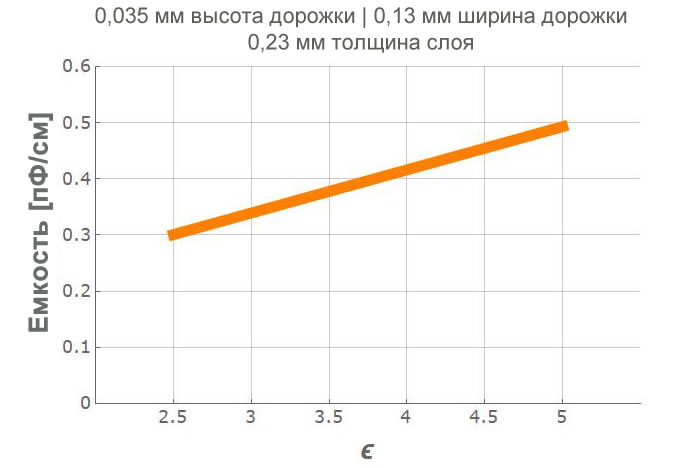
Данный график показывает влияние относительной диэлектрической проницаемости на емкость микрополосковой линии

Более дорогие базовые материалы имеют тенденцию к снижению общей диэлектрической проницаемости, что снижает общую емкость ваших дорожек на печатной плате, что и является целью. Можно уменьшить общую емкость дорожки на 45%, выбрав TLT (ε=2,5) вместо Policlad 370HR (ε_FR4=4,5).

Источники увеличения емкости шины

Источники емкости шины включают в себя микросхемы на шине, микрополосковые трассы и близлежащие сигнальные трассы и силовые полигоны. Кроме того, нельзя игнорировать емкостные эффекты краев, если в случае маленькой печатной платы дорожки микросхемы находятся близко к краю платы.

Любой метал или диэлектрик вблизи линий I2C может увеличить общую емкость, но во многих случаях этот эффект пренебрежимо мал.

Незначительные источники емкости

Паразитная связь и емкость корпусов – это не то, что вы можете контролировать. К счастью, это всего лишь 1-2 пФ на сигнальную линию. Другими словами, это не будет существенным фактором в вашей общей схеме. Эта емкость 1-2 пФ включена в оценку в следующем параграфе.

Источники существенной емкости

Микросхемы, используемые в схеме

Спецификация NXP указывает «максимальную емкость для каждого вывода ввода/вывода» 10 пФ. Каждая добавленная вами микросхема увеличит общую емкость шины примерно на 10 пФ (смотрите техническое описание для конкретной микросхемы), затем вы также должны рассмотреть емкость, связанную с дорожками, которые соединяют эту микросхему с шиной.

Емкость медной дорожки

Когда мы здесь говорим о «емкости медной дорожки», то имеем в виду одиночную дорожку над диэлектриком над полигоном земли на печатной плате. Емкостная связь между сигнальными линиями I2C и плоскостью земли может быть существенной, если микросхемы находятся далеко друг от друга, или если на шине I2C находятся несколько микросхем. Для длинных расстояний отделяйте линии I2C друг от друга расстоянием, равным нескольким ширинам дорожек (или размещайте между сигнальными трассами трассы V_dd и земли), чтобы уменьшить емкостные эффекты связи между двумя сигнальными линиями.

Чтобы вычислить емкостную связь между сигнальной трассой и плоскостью земли (или плоскостью питания) используйте следующую формулу, которая учитывает эффекты краев.

\[C[пФ] \approx \frac{0.264\tfrac{[пФ]}{[см]}(\epsilon_r+1.41)}{\ln\left(\frac{0.598\tfrac{1}{[мм]}\cdot \text{высота_слоя}} {0.08\tfrac{1}{[мм]} \cdot \text{ширина_дорожки}+0.1\tfrac{1}{[мм]}\cdot \text{толщина_дорожки}}\right)}\]

Формула модифицирована из «High Speed Digital Design» Джонсона и Грэхема.

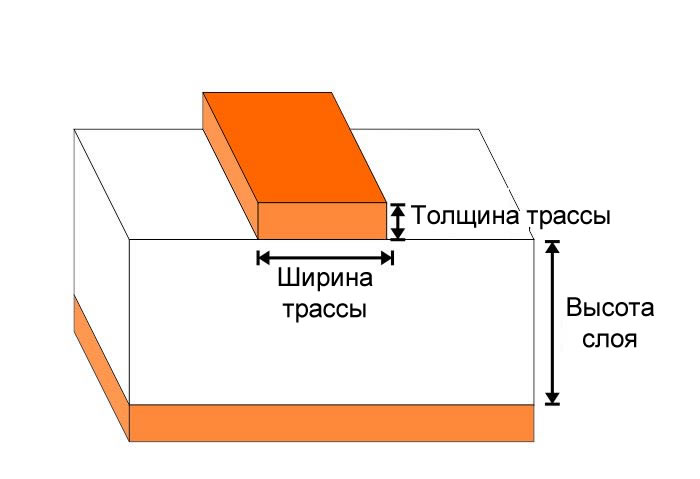
Ниже приведен расчет для смежных слоев четырехслойного стека со следующими реалистичными параметрами: ε_FR4 = 4,5, ширина дорожки = 0,13 мм, высота слоя = 0,23 мм, толщина дорожки = 0,035 мм.

\[C[пФ] \approx \frac{0.264\tfrac{[пФ]}{[см]}(4.5+1.41)}{\ln\left(\frac{0.598\tfrac{1}{[мм]}\cdot 0.23\text{[мм]}} {0.08\tfrac{1}{[мм]} \cdot 0.13\text{[мм]}+0.1\tfrac{1}{[мм]}\cdot 0.035\text{[мм]}}\right)}=0.68\tfrac{пФ}{см}\]

Влияние апертур на емкость микрополосковой линии

Можно уменьшить емкость, увеличив расстояние до плоскости земли – это достигается путем помещения сигнальных трасс на слои, которые отделены от слоя земли одним или несколькими слоями. Также можно удалять медь из слоев металлизации, чтобы создать медную пустоту под дорожкой. Эта пустота называется апертурой.

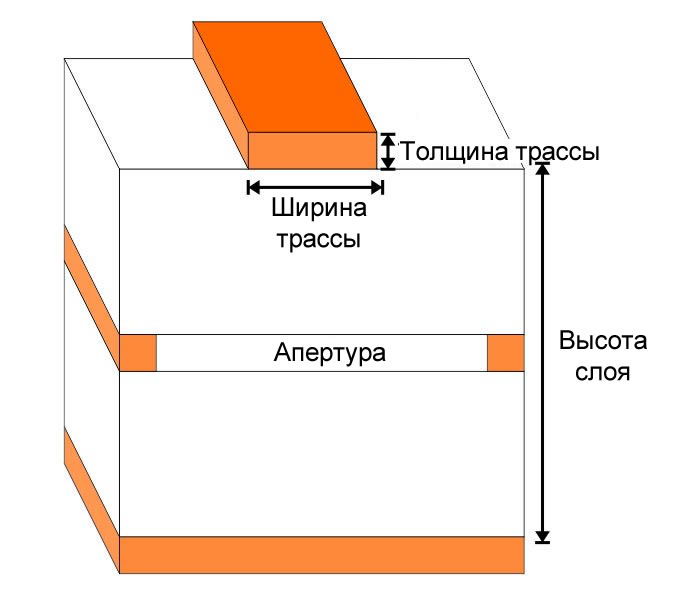
Итак, какое влияние это оказывает на общую емкость? Если мы используем те же параметры, что и в предыдущем расчете, но добавим 0,965 мм между сигнальной дорожкой и плоскостью земли, мы достигнем уменьшения емкости на ~40%. Если слой на вашей печатной плате позволяет иметь достаточно большой проем непосредственно под сигнальной дорожкой, это может быть целесообразным улучшением в проектах с очень длинными трассами.

\[C[пФ] \approx \frac{0.264\tfrac{[пФ]}{[см]}(4.5+1.41)}{\ln\left(\frac{0.598\tfrac{1}{[мм]}\left (0.23\text{[мм]}+0.035 \text{[мм]}+0.93\text{[мм]}\right )} {0.08\tfrac{1}{[мм]} \cdot 0.13\text{[мм]}+0.1\tfrac{1}{[мм]}\cdot 0.035\text{[мм]}}\right)}=0.40\tfrac{пФ}{см}\]

Резисторы

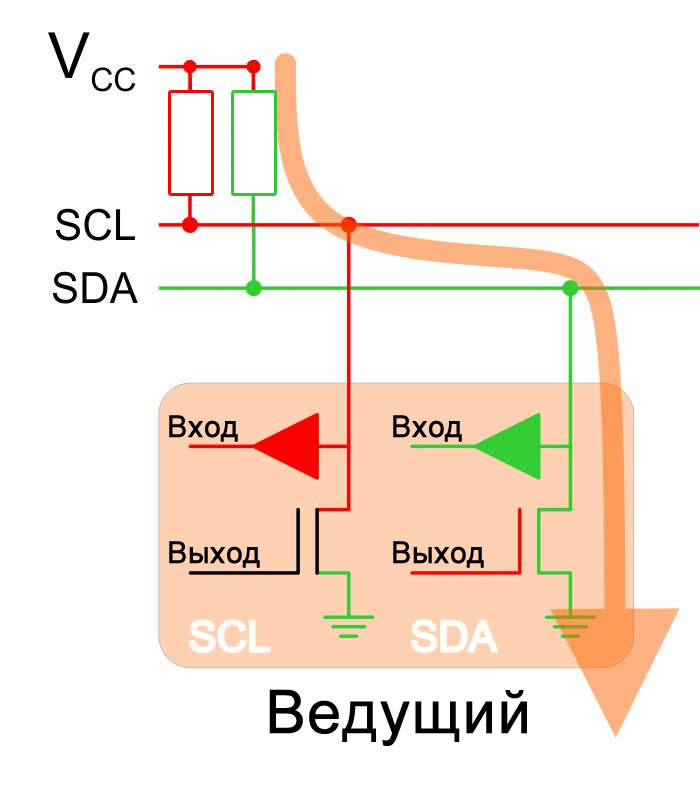
Минимальное сопротивление подтягивающего резистора определяют два требования. Во-первых, подтягивающий резистор должен ограничивать ток до уровня, который не превышает максимальный ток стока выходного транзистора. Во-вторых, резистор должен предотвращать чрезмерное потребление тока, когда сигналы SDA и SCL находятся в низком логическом состоянии. На практике потребление тока является доминирующим фактором, поскольку обычно нет необходимости использовать сопротивление, которое достаточно мало, чтобы подвергнуть выходной транзистор опасности.

В качестве примера предположим, что у нас есть шина с напряжением 3,3 В, и мы хотим ограничить ток до 3 мА.

\[R_{min}=\frac{V_{\text{шины}}}{I_{\text{max}}}=\frac{3.3\text[В]}{3\text{[мА]}}=1.1 кОм\]

Если предположить, что сигналы на тактовой и сигнальной линиях имеют коэффициент заполнения 50%, потребляемая мощность будет равна:

\[P=0.5\cdot2\cdot\frac{V^2}{R}=\frac{(3.3 [В])^2}{1100[Ом]}\approx 10\text[мВт]\]

Подтягивающие резисторы с низкими номиналами обеспечивают более быстрые переходы и «более прямоугольный» сигнал, но также приводят к более высокой рассеиваемой мощности

Расчет максимального значения подтягивающих резисторов

Чтобы обеспечить надлежащую работу, разработчик должен убедиться в том, что выполнены временны́е требования I2C устройства

На приведенном выше графике показаны сегменты переходов I2C, которые соответствуют времени нарастания, времени спада, времени, проведенному в состоянии низкого логического уровня, и времени, проведенному в состоянии высокого логического уровня. Соответствующие значения для этих временных параметров обычно указаны в техническом описании устройства. График не в масштабе.

Подтягивающие резисторы с высокими номиналами увеличат время перехода к пороговому уровню высокого логического состояния, что может помешать правильной работе микросхемы.

Время нарастания до высокого логического уровня слишком велико, и напряжение не доходит порогового уровня высокого логического состояния. Следовательно, устройства на этой шине не смогут общаться.

Вычисление максимального значения подтягивающего резистора требует знания требований к времени нарастания. Затем используются экспоненциальные функции для моделирования кривой и нахождения времени, необходимого для достижения порогового напряжения высокого логического состояния после прохождения порогового напряжения низкого логического состояния.

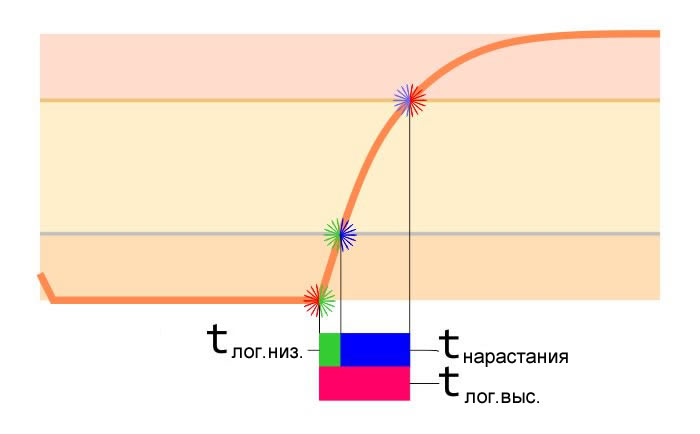
Кривая нарастания задается показанной ниже экспоненциальной функцией. Чтобы определиться со временем нарастания, вычтите время, необходимое для достижения порога высокого логического уровня из времени, необходимого для достижения порога низкого логического уровня. Формула показывает, как значения на вертикальной оси (напряжение) зависят от значений на горизонтальной оси (время). Перед определением разницы во времени необходимо выразить из этой формулы время.

\[V_{\text{лог.выс.}}=V_{\text{cc}}\left (1−e^{\left ( \frac{−t_{\text{лог.выс.}}}{R_{\text{подтяг.}}\cdot C_{\text{шины}}}\right )} \right)\]

\[t_{\text{лог.выс.}}=C_{\text{шины}}\cdot R_{\text{подтяг.}}\cdot \ln\left ( \frac{V_{\text{CC}}}{V_{\text{CC}}−V_{\text{лог.выс.}}}\right )\]

Из начальной формулы выражено время, необходимое для достижения порогового напряжения высокого логического состояния.

\[V_{\text{лог.низ.}}=V_{\text{cc}}\left (1−e^{\left ( \frac{−t_{\text{лог.низ.}}}{R_{\text{подтяг.}}\cdot C_{\text{шины}}}\right )} \right)\]

\[t_{\text{лог.низ.}}=C_{\text{шины}}\cdot R_{\text{подтяг.}}\cdot \ln\left ( \frac{V_{\text{CC}}}{V_{\text{CC}}−V_{\text{лог.низ.}}}\right )\]

Из начальной формулы выражено время, необходимое для достижения порогового напряжения низкого логического состояния.

Выразим R_{подтяг.} и получим:

\[R_{\text{подтяг. max}}=\frac{t_{\text{нарастания}}}{\ln\left ( \frac{V_{\text{cc}}−V_{\text{лог.низ.}}}{V_{\text{cc}}−V_{\text{лог.выс.}}} \right )\cdot C_{\text{шины}}}\]

Это окончательная формула, используемая в расчетах для максимального сопротивления подтягивающего резистора; t_{нарастания}, V_{лог.низ.} и V_{лог.выс.} приведены в техническом описании, а C_шины оценивается на основе характеристик вашей схемы. Выбрав произвольные значения t_{нарастания} = 150 нс, V_{лог.низ.} = 0,5 В и V_{лог.выс.} = 1,2 В, и предположив, что емкость шины составляет 150 пФ, мы получим следующее:

\[R_{\text{подтяг. max}}=\frac{150\cdot10^{-9}[с]}{\ln \left ( \frac{3.3 [В]-0.5[В]}{3.3 [В]-1.2 [В]}\right ) \cdot150\cdot 10^{-12}[Ф]}\approx 3500[Ом]\]

Резюме

Величина подтягивающего резистора I2C должна быть достаточно большой, чтобы уменьшить ненужное потребление тока, и достаточно маленькой, чтобы обеспечить приемлемое время нарастания. Расчеты, представленные в данной статье, могут помочь вам найти подходящее значение, но если вы хотите действительно оптимизировать свою шину I2C , вам, вероятно, потребуется измерить сигналы с помощью осциллографа (если возможно, используйте пробник с низкой емкостью) и отрегулировать подтягивающее сопротивление до тех пор, пока не достигнете желаемых характеристик времени.