Калькулятор волнового сопротивления микрополосковой линии (формула Хаммерстада-Дженсена)
Данный калькулятор поможет вам рассчитать волновое сопротивление (импеданс) микрополосковой линии.
Расчет
Входные данные:
Результаты:
Обзор
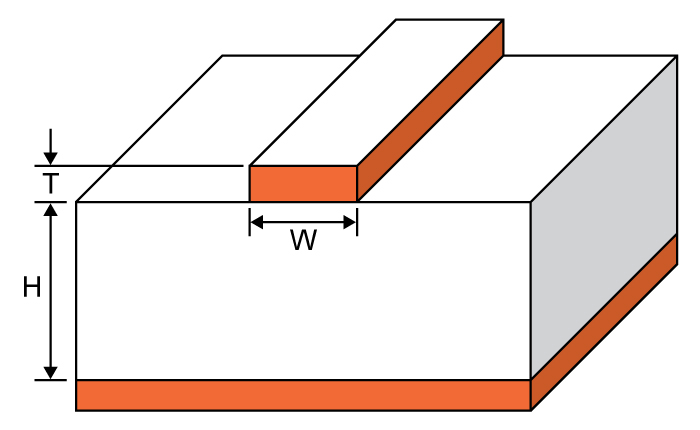
Данный калькулятор предназначен для расчета волнового сопротивления (импеданса) микрополосковой линии – плоского проводника, находящегося над полигоном земли с диэлектриком между ними (смотрите рисунок ниже). Хотя эта конструкция обычно изготавливается на базе печатных плат, она также может быть построена с использованием других материалов, если имеется проводник, отделенный от полигона земли некоторым диэлектрическим материалом.
Просто введите указанные значения толщины и ширины проводника (дорожки), высоты диэлектрической подложки и относительную диэлектрическую постоянную материала диэлектрика и нажмите кнопку «Расчет».
Данный калькулятор основан на уравнениях Э.Хаммерстада и О.Дженсена импеданса микрополосковой линии в однородной среде и эффективной диэлектрической проницаемости микрополосковой линии. Полученная точность расчетов дает ошибки, по меньшей мере, меньшие, чем ошибки, вызванные физическими отклонениями, и лучше 0,01% для W/H ≤ 1 и 0,03% для W/H ≤ 1000.
Формулы
Импеданс микрополосковой линии
\[Z_L (W,H,T,\varepsilon_r) = { Z_{L1}(W_r,H) \over \sqrt{\varepsilon_{r\_эфф}(W_r,H,\varepsilon_r)} }\]
Волновое сопротивление микрополосковой линии в однородной среде
\[Z_{L1}(W_r,H)= \frac{Z_0}{2\pi} \cdot \ln \left( f_u \frac{H}{W_r} + \sqrt{1 + \left( \frac{2H}{W_r}\right)^2} \right)\]
\[f_u = 6 + (2\pi - 6) \cdot \exp \left( - \left( 30,666 \cdot \frac{H}{W_r} \right)^{0,7528} \right)\]
Эффективная относительная диэлектрическая проницаемость изолирующего материала подложки
\[\varepsilon_{r\_эфф}(W_r,H,\varepsilon_r)= \frac{\varepsilon_r + 1}{2} + \frac{\varepsilon_r - 1}{2} \cdot \left( 1 + 10 \frac{H}{W_r} \right)^{-ab}\]
\[a(u) = 1 + \frac{1}{49} \ln\left( {u^4 + (u/52)^2 \over u^4 + 0,432} \right) + \frac{1}{18,7} \ln \left( 1+ \left( \frac{u}{18,1}\right)^3 \right)\]
\[b(\varepsilon_r) = 0,564 \cdot \left( {\varepsilon_r - 0,9 \over \varepsilon_r + 3} \right)^{0,053}\]
\[u = \frac{W}{H}\]
Эффективная ширина микрополосковой линии
\[W_r = W +\Delta W_r\]
\[\Delta W_r = \frac{1}{2} \Delta W_1 (1 + \text{sch} \sqrt{\varepsilon_r-1})\]
\[\Delta W_1 = \frac{T}{H \cdot \pi} \ln \left( 1 + {4e \over \frac{T}{H} \cdot \text{cth}^2\sqrt{6,517W} } \right)\]
где
- ZL – волновое сопротивление микрополосковой линии в омах (Ом);
- ZL1 – волновое сопротивление микрополосковой линии в однородной среде в омах (Ом)
- Z0 – волновое сопротивление вакуума, \(120\pi\) Ом;
- εr – относительная диэлектрическая проницаемость изолирующего материала подложки;
- H – высота подложки в миллиметрах (мм);
- W – ширина микрополосковой линии в миллиметрах (мм);
- T – высота микрополосковой линии в миллиметрах (мм);
- Wr – эффективная ширина микрополосковой линии, которая равна фактической ширине линии плюс поправка для учета не нулевой толщины металлизации, в миллиметрах (мм);
- εr_'эфф – эффективная относительная диэлектрическая проницаемость изолирующего материала подложки;
Применение
С помощью микрополосковых линий могут создаваться СВЧ антенны и ответвители, а также некоторые фильтры. Поскольку микрополосковые линии представляют собой просто фигуры металлизации на подложке, они намного дешевле традиционных волноводов, а также более компактны и легче. Тем не менее, микрополосковые линии не могут обрабатывать такие высокие уровни мощности, как волноводы. Микрополосковые линии также имеют проблемы с потерями мощности, перекрестными помехами и непреднамеренным излучением, поскольку они не заключены в экран, как волновод.
Помимо применения в СВЧ, микрополосковые линии также можно найти в конструкциях высокоскоростных цифровых печатных плат. Такое применение влечет за собой перемещение сигнала с минимальными искажениями и отсутствием перекрестных помех и/или излучения – области, где микрополосковые лини отличаются превосходством, пока не обрабатываются очень высокие частоты.
