Daily bit(e) C++. Обход в порядке столбцов

Добавлено 25 сентября 2023 в 09:54

Daily bit(e) C++ #14, распространенный вопрос на собеседованиях: обход в порядке столбцов.

Сегодня мы рассмотрим еще один распространенный вопрос на собеседованиях – обход двоичного дерева по столбцам.

Дано двоичное дерево, реализуйте обход дерева в порядке столбцов. Узлы следует проходить в порядке их столбца, где столбец дочернего элемента равен -1 (для левого дочернего элемента) или +1 (для правого дочернего элемента) от его родителя. Узлы в одном столбце следует обходить в порядке по их расстоянию от корневого узла или по значению узла, если они находятся на одинаковом расстоянии от корня.

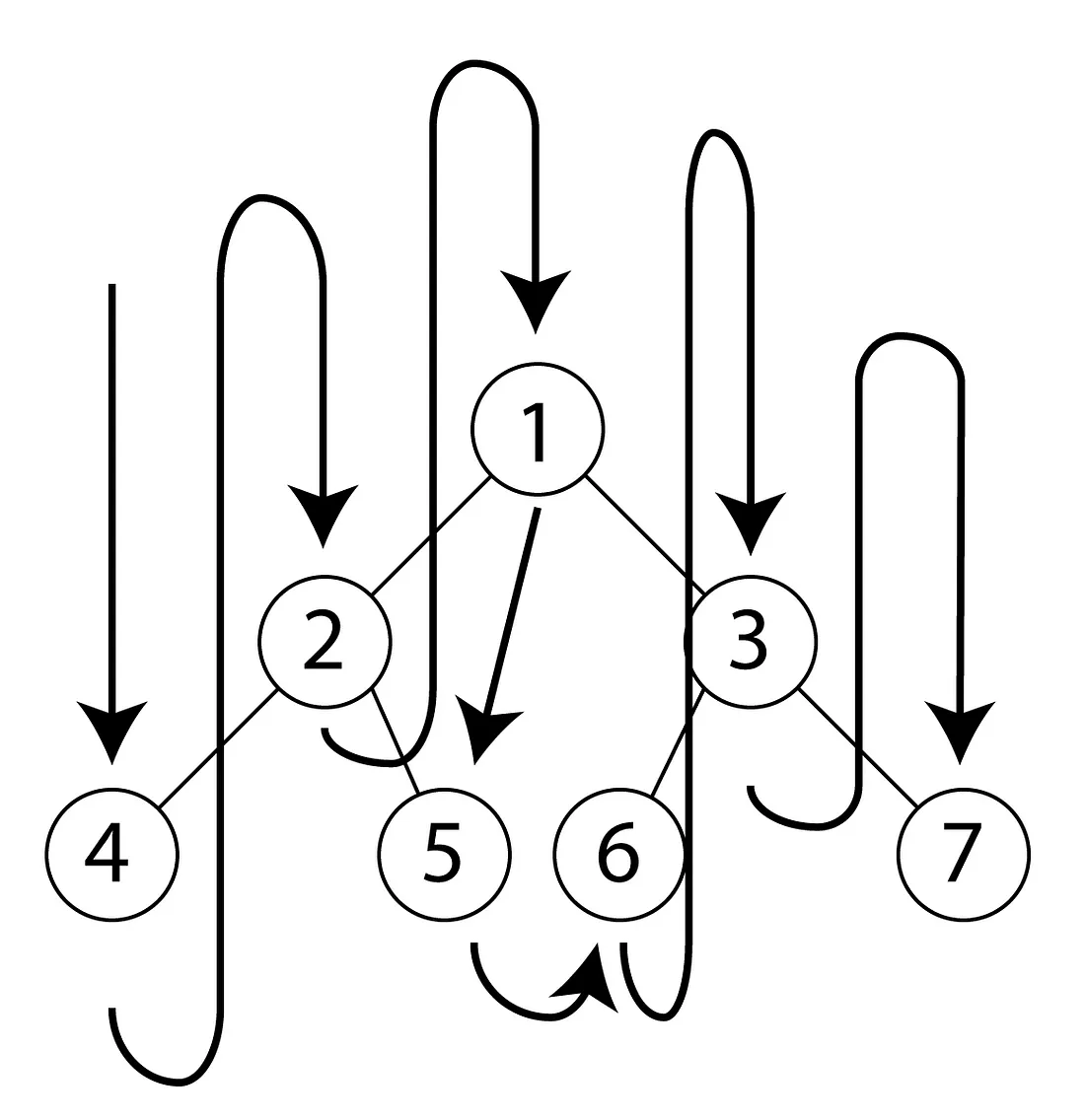
Например, порядок обхода по столбцам для этого дерева будет таким: {4, 2, 1, 5, 6, 3, 7}.

Прежде чем прочитать решение, попробуйте решить задачу самостоятельно. Вот ссылка на Compiler Explorer с парой тестовых случаев: https://compiler-explorer.com/z/zEGMnx3jn.

Решение

Основная сложность, с которой мы сталкиваемся, – это то, что независимо от того, на каком этапе обхода мы находимся, у нас должна быть возможность добраться до любого столбца.

Это фактически заставляет нас сортировать узлы (каким-то образом).

Самый простой подход к сортировке узлов – использовать упорядоченную структуру данных (например, std::set или std::priority_queue). Каждая вставка в упорядоченную структуру данных равна O(logn), а поскольку мы будем вставлять каждый узел, конечная сложность составит O(n*logn).

После заполнения этой нашей структуры данных мы можем пройти по ней за линейное время, посещая каждый узел.

#include <vector>
#include <functional>
#include <set>

// Информация об узле используется для хранения
// узлов в порядку столбцов
struct NodeInfo 
{
    int column;
    int row;
    Node* node;
    friend auto operator<=>(const NodeInfo& l, const NodeInfo& r) 
    {
        auto c1 = l.column <=> r.column;
        if (!std::is_eq(c1)) return c1;
        auto c2 = l.row <=> r.row;
        if (!std::is_eq(c2)) return c2;
        return l.node->value <=> r.node->value;
    }
};

// Обход дерева, сохраняем каждый узел в set
void fill(Node* node, std::set<NodeInfo>& ordered, int column, int row) 
{
    if (node == nullptr) return;
    ordered.insert({column, row, node});
    // Левый потомок находится в column-1 и
    // на расстоянии на единицу больше от корня
    fill(node->left, ordered, column-1, row+1);
    // Правый потомок находится в column+1 и
    // на расстоянии на единицу больше от корня
    fill(node->right, ordered, column+1, row+1);
}

void column_order(const Tree& tree, std::function<void(Node*)> visitor) 
{
    std::set<NodeInfo> ordered;
    // Заполняем структуру данных, каждая вставка - это log(n) -> O(n*logn)
    fill(tree.root, ordered, 0, 0);
    // Обход структуры данных O(n)
    for (auto &v : ordered) 
    {
        visitor(v.node); // посещаем узел, обрабатывая его
    }
}

Открыть решение на Compiler Explorer.

Решение

Теги