Daily bit(e) C++. Поиск всех узлов на расстоянии K в двоичном дереве

Добавлено 24 сентября 2023 в 05:40

Daily bit(e) C++ #226, распространенная задача на собеседованиях: найти все узлы на расстоянии K в двоичном дереве.

Сегодня мы рассмотрим распространенную задачу на собеседованиях по C++: найти все узлы на расстоянии K в двоичном дереве.

Дано двоичное дерево, содержащее уникальные целочисленные значения, верните все узлы, находящиеся на расстоянии K от заданного узла N.

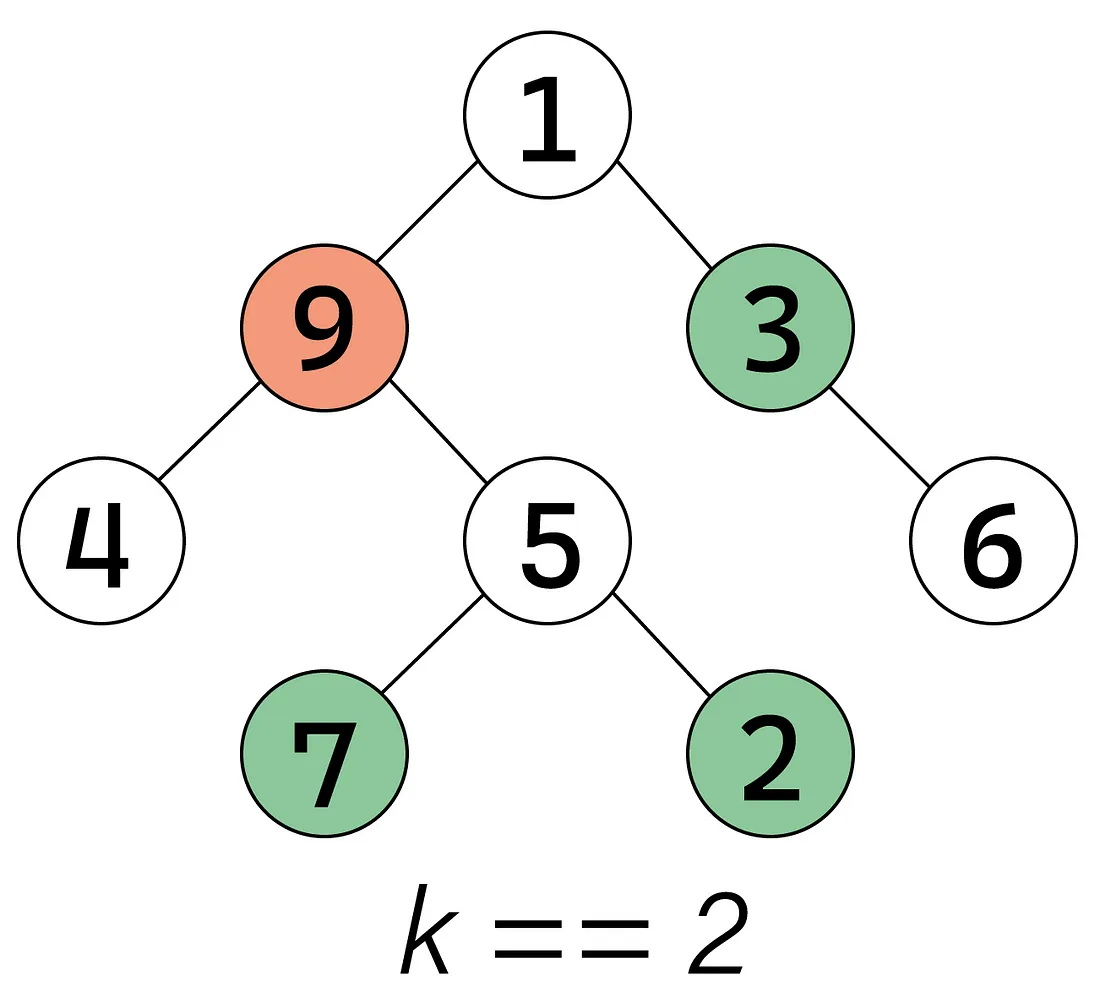
Например, в приведенном выше дереве три узла находятся на расстоянии два от узла девять: {2,3,7}.

Прежде чем прочитать решение, советую попытаться решить задачу самостоятельно. Вот ссылка на Compiler Explorer с парой тестовых случаев: https://compiler-explorer.com/z/8recYWq9r.

Решение

Один из вариантов – преобразовать двоичное дерево, по сути, ориентированный граф, в неориентированный граф, в котором мы можем легко найти узлы на расстоянии k, применив поиск в ширину.

Однако у нас есть более простой вариант, основанный на следующем наблюдении. Рассмотрим узел с одним из его дочерних элементов. Если дочерний узел не лежит на пути между узлом и нашей целью, его расстояние до цели просто на единицу больше, чем расстояние родительского узла. Если он лежит на пути между узлом и целью, его расстояние на единицу меньше.

Если мы исследуем граф, используя прямой (pre-order) обход, у нас также будет вторая гарантия того, что узел находится на пути только в том случае, если он также находится на пути между корнем и целевым узлом.

Используя эти наблюдения, мы можем построить двухпроходное решение.

Сначала мы находим нашу цель и инициализируем расстояния для всех узлов на пути между целью и корнем дерева.

На втором проходе, если у нас есть заранее вычисленное значение для узла, мы знаем, что он находится на пути, что позволяет нам различать две ситуации. Кроме того, когда мы встречаем узел на соответствующем расстоянии, мы запоминаем его.

// Поиск цели и построение расстояний до корня
int distance_search(Node* root, Node* target, 
                    std::unordered_map<int,int>& distances) 
{
    if (root == nullptr)
        return -1;
    if (root == target) 
    {
        distances[root->value] = 0;
        return 0;
    }
    // Цель в левом поддереве
    if (int left = distance_search(root->left, target, distances);
        left >= 0) 
    {
        distances[root->value] = left + 1;
        return left + 1;
    }
    // Цель в правом поддереве
    if (int right = distance_search(root->right, target, distances);
        right >= 0) 
    {
        distances[root->value] = right + 1;
        return right + 1;
    }
    // Цель не в этом поддереве
    return -1;
}

// Второй проход. 
void dfs(Node* root, Node* target, int k, int dist,
         std::unordered_map<int,int>& distances,
         std::vector<int>& result) 
{
    if (root == nullptr) return;
    // Проверка, лежит ли этот узел на пути к цели.
    auto it = distances.find(root->value);
    // Узел лежит на пути к цели, обновить расстояние.
    if (it != distances.end())
        dist = it->second;
    // Этот узел лежит на расстоянии k от цели.
    if (dist == k)
        result.push_back(root->value);

    // Расстояния до детей на единицу больше, если только
    // они не находятся на пути, обработанном выше.
    dfs(root->left, target, k, dist + 1, distances, result);
    dfs(root->right, target, k, dist + 1, distances, result);
}

std::vector<int> find_distance_k_nodes(
  Node* root, Node* target, int k) 
{
    // Первый проход
    std::unordered_map<int,int> distances;
    distance_search(root, target, distances);
    // Второй проход
    std::vector<int> result;
    dfs(root, target, k, distances[root->value], distances, result);
    return result;
}

Открыть решение на Compiler Explorer.

Решение

Теги