Daily bit(e) C++. Самый большой прямоугольник на гистограмме

Daily bit(e) C++ #217, распространенная задача на собеседованиях: самый большой прямоугольник на гистограмме.

Сегодня мы рассмотрим распространенную задачу на собеседованиях по C++: самый большой прямоугольник на гистограмме.

Дана гистограмма в виде std::vector<int>, где каждый элемент представляет высоту столбца с индексом i.

Определите размер самого большого прямоугольника, который можно нарисовать внутри этой гистограммы.

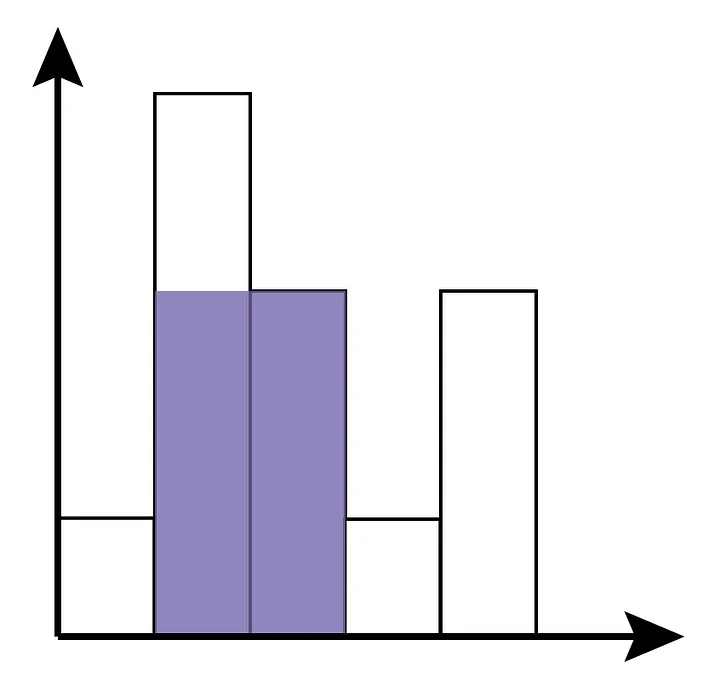
Например, для входных данных {1, 5, 4, 1, 4} максимальный прямоугольник имеет размер восемь и охватывает элементы {5, 4}.

Прежде чем прочесть решение, советую попытаться решить задачу самостоятельно. Вот ссылка на Compiler Explorer с парой тестовых случаев: https://compiler-explorer.com/z/jf31TGj5E.

Решение

Давайте сначала рассмотрим простой сценарий, когда значения на гистограмме строго возрастают. В таком случае у нас есть n потенциальных прямоугольников, по одному на каждую уникальную высоту. Каждый из прямоугольников ограничен элементом слева и концом гистограммы справа.

Если мы добавим одинаковые значения, сделав гистограмму монотонной, мы всё равно сможем применить ту же логику; однако теперь мы хотим рассматривать только последний элемент с каждым уникальным значением (потому что этот элемент создаст левую границу для следующего более высокого значения).

Наконец, давайте рассмотрим случай, когда у нас есть три последовательных элемента со значениями A, B и C, где A < B && B > C. В этом случае прямоугольник высотой B ограничен позициями элементов A и C.

Это очень убедительно указывает на монотонную структуру данных стека. Мы можем сканировать гистограмму слева направо, применяя следующую логику:

• Если текущий элемент имеет то же значение, что и вершина стека, удалите вершину. Добавьте текущий элемент в стек в качестве новой левой границы для следующего более высокого значения.
• Если текущий элемент ниже вершины стека, он создает правую границу для некоторых элементов стека. Мы должны обработать все такие элементы, чтобы вернуть стек в строго возрастающее состояние.
• Если текущий элемент выше вершины стека, мы добавляем его в стек.

В итоге у нас остается строго возрастающая последовательность элементов в нашем стеке, или, точнее, с точки зрения удаления элементов из стека, строго убывающая последовательность. Затем мы можем обработать элементы; каждый ограничен следующим элементом в стеке и правой границей гистограммы.

int max_rectangle(const std::vector<int>& heights) 
{
    std::stack<int64_t> stack;

    // Вместо неявной левой границы гистограммы,
    // мы можем сделать левую границу явной.
    stack.push(-1);
    int max_area = 0;

    // Обрабатываем все элементы
    for (int64_t i = 0; i < std::ssize(heights); ++i) 
    {
        while (stack.top() != -1 && 
               heights[stack.top()] >= heights[i]) 
        {
            int height = heights[stack.top()];
            stack.pop();
            // Ограничен текущим элементом справа и
            // следующим элементом в стеке слева.
            int width = i - stack.top() - 1;
            max_area = std::max(max_area, height*width);
        }
        stack.push(i);
    }
  
    // Здесь мы имеем строго возрастающую последовательность
    while (stack.top() != -1) 
    {
        int height = heights[stack.top()];
        stack.pop();
        // Ограничен концом гистограммы справа и
        // следующим элементом в стеке слева.
        int width = heights.size() - stack.top() - 1;
        max_area = std::max(max_area, height*width);
    }
    return max_area;
}

Открыть решение на Compiler Explorer.

Поскольку каждый элемент добавляется и удаляется из стека только один раз, мы получаем временную и пространственную сложность O(n).

Теги