Daily bit(e) C++. Количество переупорядочиваний сериализованного двоичного дерева поиска

Daily bit(e) C++ #212, распространенная задача на собеседованиях: количество переупорядочиваний сериализованного двоичного дерева поиска (binary search tree, BST).

Сегодня мы рассмотрим распространенную задачу на собеседованиях по C++: количество переупорядочиваний сериализованного двоичного дерева поиска (BST).

Задана перестановка 1..N как std::vector<int>, необходимо вернуть количество других перестановок, которые представляют то же BST. BST создается путем вставки элементов в порядке их индексов (то есть слева направо).

Поскольку количество перестановок может быть большим, возвращайте результат по модулю 10⁹+7 (остаток при делении на число 10⁹+7).

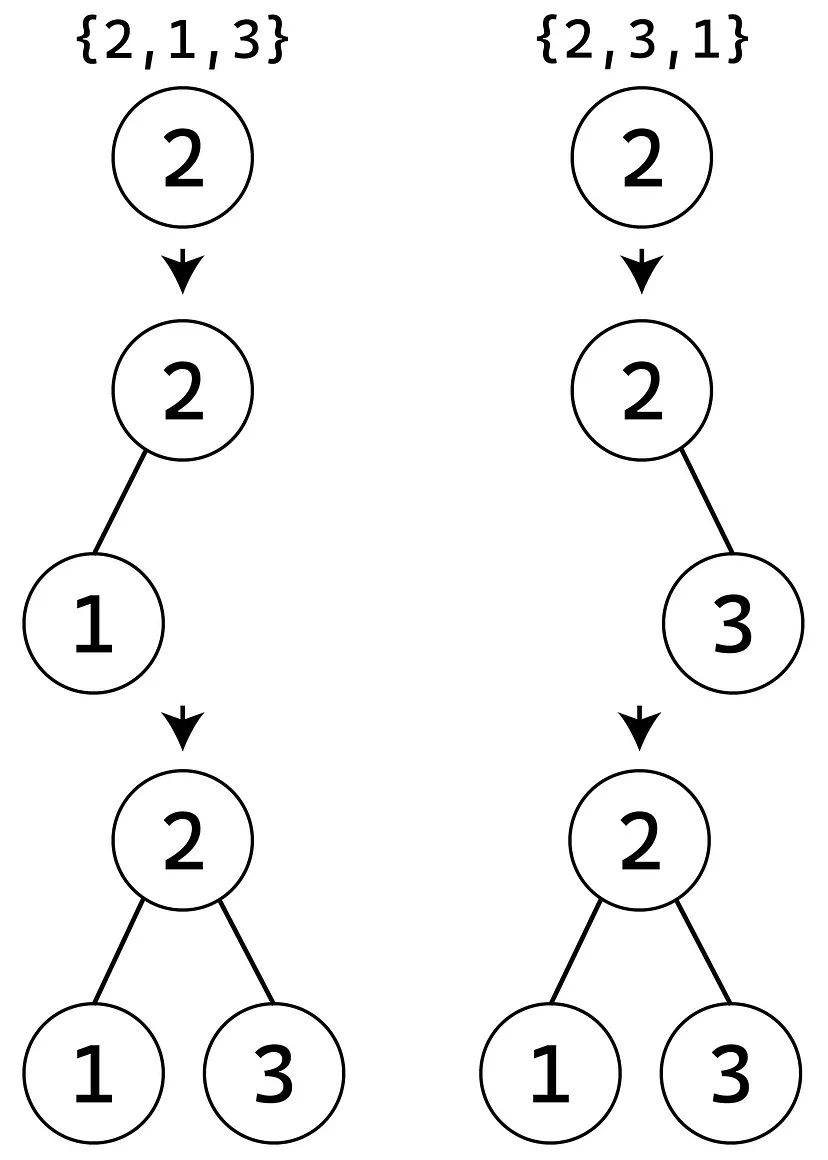
Например, для перестановки {2,1,3} есть еще одна перестановка, которая дает то же BST: {2,3,1}.

Прежде чем прочесть решение, рекомендую попробовать решить задачу самостоятельно. Вот ссылка Compiler Explorer с несколькими тестовыми случаями: https://compiler-explorer.com/z/aPjrnoafP.

Решение

Во-первых, давайте напомним себе, как работают деревья бинарного поиска. Для каждого узла все узлы левого поддерева ниже значения этого узла, а все узлы правого поддерева выше значения этого узла.

Это позволяет нам обеспечить сложность поиска любого узла с определенным значением в log(n).

Определение количества переупорядочиваний, приводящих к одному и тому же BST, гораздо менее очевидно. Однако первое довольно простое наблюдение заключается в том, что первый узел всегда будет корневым узлом, и он создает разделение других узлов (на левое и правое поддеревья).

Это указывает на то, что первая часть влияет на общее количество переупорядочений. Любое переупорядочивание элементов, создающее один и тот же стабильный раздел, приведет к одному и тому же BST.

Рассмотрим перестановку {3,1,2,4,5}. Изменение порядка элементов в каждом разделе (например, {1,2}, {4,5}) приведет к созданию разных разделов; однако мы можем свободно чередовать эти разделы без изменения результата. Более формально, мы ищем количество способов выбрать позиции для левого (или правого) раздела из всех позиций, то есть C(n-1,k) (биномиальный коэффициент), где n – общее количество элементов в перестановке, а k – количество элементов в левом разделе.

Второй момент, который мы не рассмотрели, – это количество переупорядочений в двух поддеревьях, которое мы можем вычислить рекурсивно.

Это приводит к общей формуле: reorderings(left) * reorderings(right) * coeff(n-1, left.size()).

Это означает, что нам придется предварительно вычислить биномиальные коэффициенты, что мы можем сделать, используя треугольник Паскаля.

Наконец, нам нужно применить запрошенную операцию по модулю, где это уместно.

#include <vector>
#include <span>
#include <algorithm>

constexpr inline int32_t mod = 1e9+7;

int32_t count(std::span<int> nums, 
              std::vector<std::vector<int>>& coef) 
{
    if (nums.size() < 3) return 1;

    // Разделить на левого и правого потомка
    auto rng = std::ranges::stable_partition(nums, 
        [pivot = nums[0]](int v) { return v < pivot; });
    auto left = std::span(nums.begin(), rng.begin());
    // Пропустить первый элемент, так как
    // он является родительским узлом
    auto right = std::span(rng.begin()+1, nums.end());

    // Вычислить количество переупорядочиваний для обоих поддеревьев
    int64_t left_cnt = count(left, coef) % mod;
    int64_t right_cnt = count(right, coef) % mod;
    // Примечание: здесь нам нужно 64 бита,
    // потому что нам нужно поместить 32 бит * 32 бит
    // в приведенный ниже расчет.
  
    // The result is:
    // left * right * number of ways to pick positions
    // for left.size() elements in nums.size()-1 positions.
    // Результат:
    // количество переупорядочиваний слева * 
    //     количество переупорядочиваний справа *
    //     количество способов выбора позиций для
    //     элементов left.size() в позиции nums.size()-1.
    return ((left_cnt*right_cnt) % mod)
      *coef[nums.size()-1][left.size()] % mod;
}

int32_t number_of_reorders(std::span<int> nums) 
{
    // Предварительно вычислить биномиальные коэффициенты
    // до nums.size()-1
    std::vector<std::vector<int>> binomial_coefficients;
    binomial_coefficients.resize(nums.size());
    for (int64_t i = 0; i < std::ssize(nums); ++i) 
    {
        binomial_coefficients[i].resize(i+1, 1);
        for (int64_t j = 1; j < i; ++j)
        {
            // треугольник Паскаля
            binomial_coefficients[i][j] = 
                (binomial_coefficients[i-1][j-1] + 
                 binomial_coefficients[i-1][j]) % mod;
        {
    }

    return (count(nums, binomial_coefficients)-1) % mod;
}

Открыть решение на Compiler Explorer.

Теги