Daily bit(e) C++. Самый короткий путь ко всем ключам

Daily bit(e) C++ #210, распространенная задача на собеседованиях: кратчайший путь ко всем ключам.

Сегодня мы рассмотрим распространенную задачу на интервью по C++: кратчайший путь ко всем ключам.

Задана карта, представленная как std::vector<std::vector<char>>, где:

• # – непроходимые стены;
• @ – это вход в лабиринт;
• первые k строчных букв – это ключи;
• соответствующие заглавные буквы – запертые двери.

Предполагая, что k <= 6, определите длину кратчайшего пути, который собирает все ключи, либо верните -1, если таковых путей не существует.

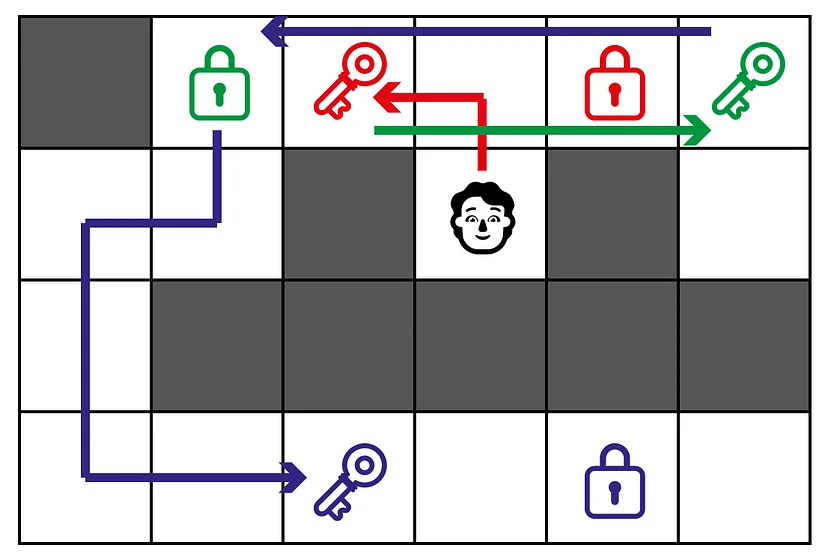
Например, на приведенной выше карте мы сначала должны взять красный ключ (2 шага), затем зеленый ключ (3 шага) и, наконец, синий ключ (10 шагов).

Прежде чем прочесть решение, рекомендую попробовать решить задачу самостоятельно. Вот ссылка на Compiler Explorer с несколькими тестовыми случаями: https://godbolt.org/z/9dW6Gzrer.

Решение

Определение кратчайшего пути – это из сферы поиска в ширину. Однако ключи вносят усложнение.

Мы могли бы попытаться разобраться с ключами; однако у нас есть очень консервативная оценка количества ключей (шесть).

Поэтому мы можем применить многомерный прием для поиска в ширину. Когда мы попадаем на клетку с ключом, мы можем перейти на этаж лабиринта, в котором никогда не было соответствующей двери. Есть 2^k уникальных этажей, что для нашей верхней границы дает максимум 64 этажа.

С этим трехмерным лабиринтом мы можем применить стандартный поиск в ширину, что приводит к временной и пространственной сложности O(m*n*2^k).

struct Coord 
{
    int64_t row;
    int64_t col;
};

struct Pos
{
    int64_t row;
    int64_t col;
    std::bitset<6> keys;
    int64_t dist;
};

int64_t shortest_path(const std::vector<std::vector<char>>& grid) 
{
    // Сканируем карту, чтобы определить количество ключей
    // и положение стартовой позиции.
    int k = 0;
    Coord start;
    for (int64_t i = 0; i < std::ssize(grid); ++i) 
    {
        for (int64_t j = 0; j < std::ssize(grid[i]); ++j) 
        {
            if (std::islower(grid[i][j]))
                k = std::max(k, grid[i][j]-'a'+1);
            if (grid[i][j] == '@')
                start = {i,j};
        }
    }

    // Отслеживание посещенных клеток
    std::vector<std::vector<std::vector<bool>>> visited(
        grid.size(), std::vector<std::vector<bool>>(
            grid[0].size(), std::vector<bool>(64, false)
        ));

    // алгоритм поиска в ширину
    std::queue<Pos> bfs;
    // Начинаем в точке start с нулем ключей
    bfs.push({start.row, start.col, 0, 0});
    
    while (!bfs.empty()) 
    {
        auto curr = bfs.front();
        bfs.pop();

        // Мы собрали все ключи, с первого раза делаем,
        // знаем, что это кратчайший путь.
        if (curr.keys.count() == uint64_t{k})
            return curr.dist;

        // Вспомогательная лямбда для проверки,
        // можем ли мы шагнуть на заданную клетку
        auto can_step = [&](int64_t row, int64_t col, 
                            std::bitset<6> keys) {
            // нет, выходим за границы
            if (row < 0 || col < 0 || 
                row >= std::ssize(grid) || 
                col >= std::ssize(grid[row]))
                return false;
            // нет, стена
            if (grid[row][col] == '#') return false;
            // нет, уже посещали
            if (visited[row][col][keys.to_ulong()]) return false;
            // нет, это дверь, от которой у нас нет ключа
            if (std::isupper(grid[row][col]) && 
                !keys[grid[row][col]-'A']) return false;
            return true;
        };

        auto with_key = [&](int64_t row, int64_t col, 
                            std::bitset<6> keys, int64_t dist) {
            // Если на этой клетке ключ, добавляем его себе в связку.
            if (std::islower(grid[row][col]))
                keys[grid[row][col]-'a'] = true;
            return Pos{row, col, keys, dist};
        };

        // Для каждого направления
        for (auto offset : {Coord{-1,0}, Coord{1,0}, 
                            Coord{0,-1}, Coord{0,1}}) 
        {
            // Если мы можем шагнуть на эту клетку
            if (!can_step(curr.row+offset.row, 
                          curr.col+offset.col, 
                          curr.keys)) continue;
            
            auto next = with_key(curr.row+offset.row,
                                 curr.col+offset.col, 
                                 curr.keys,
                                 curr.dist+1);

            // Отмечаем клетку как посещенную; обратите внимание,
            // что если это клетка с ключом, мы технически перемещаемся
            // в две клетки: одна, где у нас еще нет ключа, а вторая,
            // когда он у нас есть.
            visited[next.row][next.col][curr.keys.to_ulong()] = true;
            visited[next.row][next.col][next.keys.to_ulong()] = true;
            // Добавляем в очередь.
            bfs.push(next); 
        }
    }
    return -1;
}

Открыть решение на Compiler Explorer.

Теги