Daily bit(e) C++. Прыгающий мяч

Добавлено 6 августа 2023 в 19:41

Daily bit(e) C++ #7, распространенные вопросы на собеседованиях: прыгающий мяч.

Сегодня мы рассмотрим распространенную задачу на собеседованиях – «прыгающий мяч».

Задан список целей, выстроенных в линию, определите, может ли прыгающий мяч достичь конечной цели. Мяч может только отскакивать от целей, и если он достигнет цели с горизонтальной скоростью 'i', он отскочит с горизонтальной скоростью 'i-1', 'i' или 'i+1'.

Мяч никогда полностью не потеряет горизонтальной скорости вперед (то есть не отскочит назад).

Начальный бросок имеет горизонтальную скорость 1.

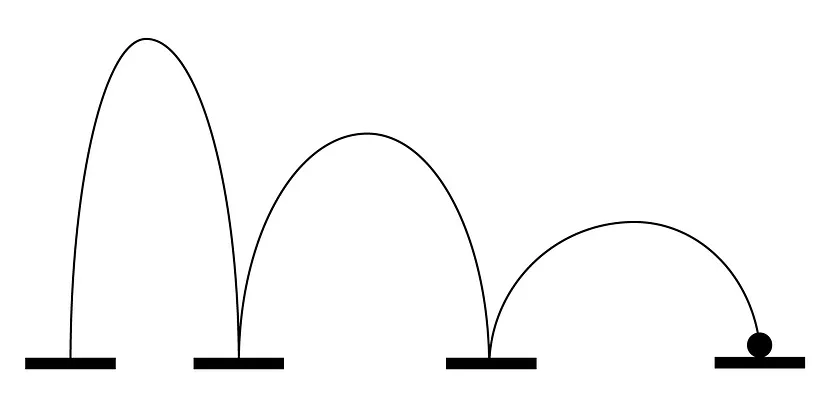
Например, для входных данных {0,1,3,4,6,9,13} мяч может достичь конечной цели следующим образом:

отскок от цели 1 со скоростью 2;
отскок от цели 3 со скоростью 1;
отскок от цели 4 со скоростью 2;
отскок от цели 6 со скоростью 3;
и, наконец, отскок от цели 9 со скоростью 4 и приземление на последнюю цель.

Для входных данных {0,1,3,7,10,14} мяч не может достичь конечной цели, так как скачок между 3 и 7 слишком велик.

Прежде чем прочитать решение, попробуйте решить задачу самостоятельно. Вот ссылка на Compiler Explorer с несколькими тестовыми случаями: https://godbolt.org/z/9x6PsheEW.

Решение

Основная сложность в этой задаче в том, что цель может быть достигнута из нескольких других целей с разной скоростью, что также приводит к разным скоростям выхода.

Однако если бы у нас был список скоростей, на которых достижима конкретная цель, построение множества достижимых целей из этой задачи тривиально.

Это уже указывает нам на решение для динамического программирования. Вначале мы знаем только, что из нашей исходной позиции достижима цель на расстоянии '1'.

Однако, поскольку мяч не может отскочить назад, мы можем выполнить итерацию по целям один раз и, используя эту информацию, когда мы достигаем каждой цели, создать базу данных скоростей, с которыми можно достичь каждую цель.

bool canReach(const std::vector<int>& targets) 
{
  // Цель -> Список скоростей, при которых она достижима
  std::unordered_map<int,std::unordered_set<int>> speeds;
  // В начале достижима только вторая цель при скорости 1.
  for (auto distance : targets | std::views::drop(1))
    speeds[distance] = {};
  speeds[1] = {1};

  // Обработка каждой цели
  for (auto distance : targets | std::views::drop(1)) 
  {
    // Для каждой скорости, на которой эта цель достижима
    for (auto speed : speeds[distance]) 
    {
      // Для каждого изменения скорости
      for (auto diff : {-1, 0, 1}) {
        if (speed + diff <= 0)
          continue;
        // Если есть цель, достижимая с этой скоростью,
        // добавляем эту скорость в список скоростей.
        if (speeds.contains(distance + speed + diff))
          speeds[distance + speed + diff].insert(speed + diff);
      }
    }
  }
  // Возвращаем, смогли ли мы достичь конечной цели.
  return !speeds[targets.back()].empty();
}

Открыть решение на Compiler Explorer.

Сложность этого решения может быть неочевидной. Наш внешний цикл выполняет итерацию по всем целям один раз, но внутренний цикл выполняет итерацию со всеми возможными скоростями. Поскольку существует только одна скорость, с которой соединяются не более двух конкретных целей, внутренний цикл будет иметь ту же сложность, что и внешний цикл.

Это приводит нас к сложности по времени O(n*n). Поскольку наши циклы напрямую отображаются на хранящихся данных, то сложность относительно памяти также получаем O(n*n).

Решение

Теги