Daily bit(e) C++. Разделение шариков

Добавлено 1 августа 2023 в 01:11

Daily bit(e) C++ # 205, Распространенная задача на собеседованиях: разделение шариков.

Сегодня мы рассмотрим распространенную задачу интервью по C++: разделение шариков.

Дан ряд шариков с разными значениями, представленный как std::vector<int64_t>, разделите эти шарики на k смежных секций.

Необходимо вернуть разницу между максимальным и минимальным значениями секций, которые можно получить, учитывая, что секция i..j имеет значение values[i]+values[j].

Учитывая, что достижима сложность O(n), необходимо предоставить решение как минимум с O(n*logn).

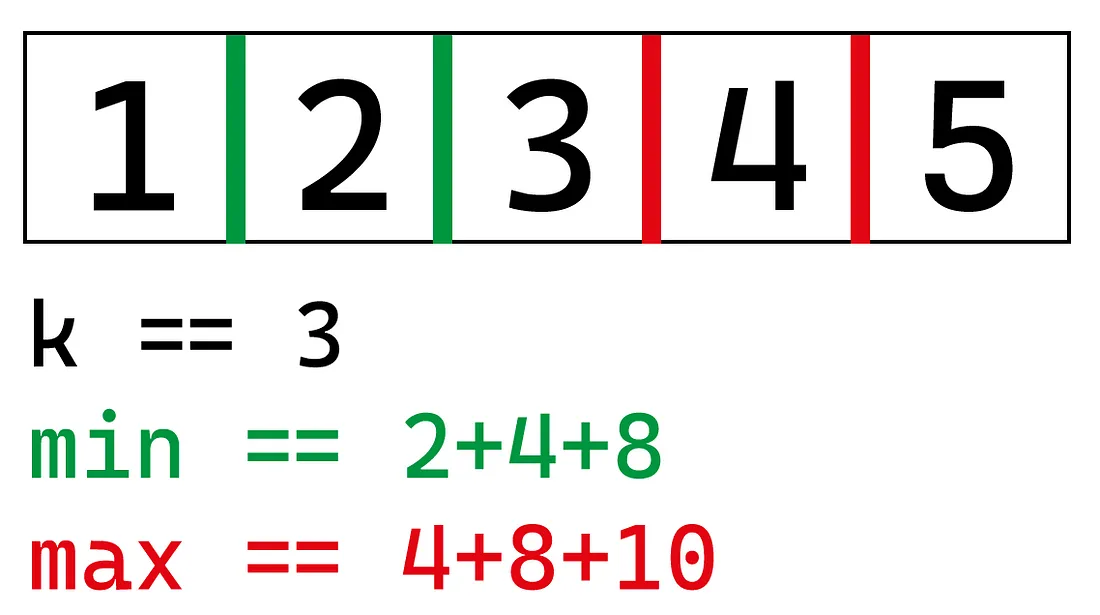
Например, для последовательности шариков со значениями {1,2,3,4,5} и количества секций k = 3 минимальное значение, которое мы можем получить, равно 14 с секциями {1}, {2}, {3,4,5}, а максимальное значение, которое мы можем получить, равно 22 с секциями {1,2,3}, {4}, {5}.

Прежде прочесть решение, я рекомендую вам попробовать решить задачу самостоятельно. Вот ссылка Compiler Explorer с несколькими тестовыми случаями: https://compiler-explorer.com/z/a8s6YPh7M.

Решение

Эта задача требует переосмысления. Что нас просят сделать?

Давайте рассмотрим общую сумму, которую мы пытаемся минимизировать и максимизировать. Это будут последовательности значений, которые всегда будут содержать values[0] и values[values.size()-1], с остальными элементами образующими смежные пары.

Поскольку перед нами стоит задача вернуть разницу, мы можем спокойно игнорировать граничные значения и сосредоточиться на смежных парах. У нас будет k-1 таких пар, и для минимума это будут k-1 пар с минимальными суммами, а для максимума это будут k-1 пар с максимальными суммами.

При этом мы можем переформулировать задачу: вернуть разницу между суммой k-1 наименьших смежных сумм и суммой k-1 наибольших смежных сумм. Это достижимо за O(n).

int64_t split_marbles(const std::vector<int64_t>& weights, int64_t k) {
    if (weights.size() < 2 || k < 2) return 0;

    // Генерируем суммы смежных элементов
    auto sums_view = weights | 
      std::views::pairwise_transform(std::plus<>{});
    std::vector<int64_t> sums(sums_view.begin(), sums_view.end());

    // Разделим sums так, чтобы следующий поддиапазон
    // представлял k-1 наименьших элементов. 
    std::ranges::nth_element(sums,
                             sums.begin()+(k-2));
    auto min_k = std::ranges::subrange(sums.begin(), 
                                       sums.begin()+(k-2)+1);
    // Минимальная сумма - это сумма этих элементов
    int64_t min = std::ranges::fold_left(min_k, int64_t{0},
                                         std::plus<>{});

    // Разделим sums так, чтобы следующий поддиапазон
    // представлял k-1 наибольших элементов. 
    std::ranges::nth_element(sums, 
                             sums.end()-(k-1));
    auto max_k = std::ranges::subrange(sums.end()-(k-1), 
                                       sums.end());
    // Максимальное значение - это сумма этих элементов
    int64_t max = std::ranges::fold_left(max_k, int64_t{0},
                                         std::plus<>{});

    // Обратите внимание, что технически фактические min и max больше,
    // оба также содержат weights[0] и weights[weight.size()-1].
    // Поскольку мы берем разницу, это не имеет значения.
    return max-min;
}

Открыть пример на Compiler Explorer.

Решение

Теги