Daily bit(e) C++. Самый длинный цикл в графе

Daily bit(e) C++ #203. Распространенная задача на собеседованиях: самый длинный цикл в графе.

Сегодня мы рассмотрим распространенную задачу на интервью по C++: самый длинный цикл в графе.

Задан ориентированный граф в виде std::vector<int>, где значение с индексом i представляет пункт назначения исходящего ребра из i (-1 используется для обозначения отсутствия исходящих ребер), необходимо определить размер самого длинного цикла в графе.

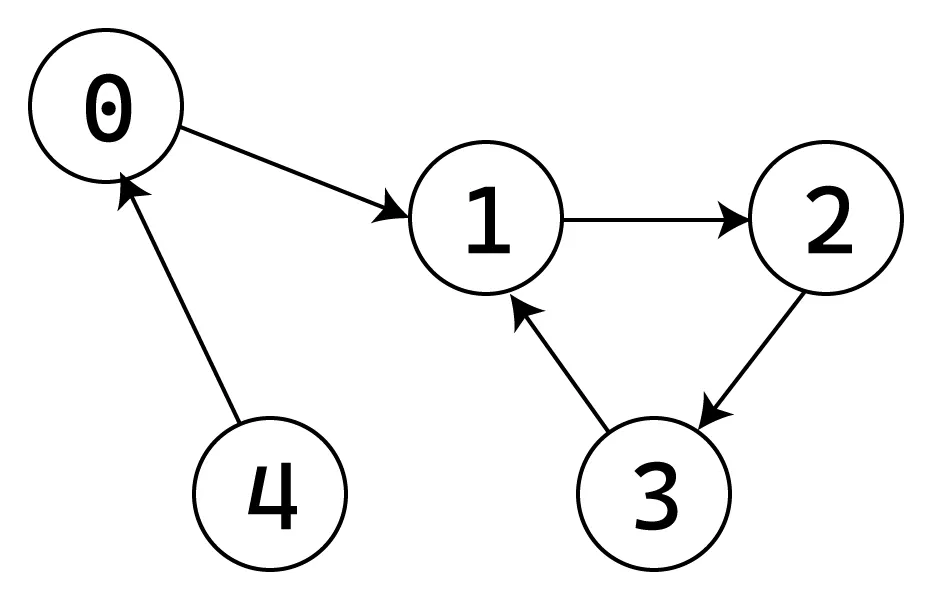
Например, приведенный выше граф представлен вектором {1,2,3,1,0}, образует цикл размером три.

Прежде чем прочесть решение, я рекомендую вам попробовать решить задачу самостоятельно. Вот ссылка на Compiler Explorer с несколькими тестовыми случаями: https://compiler-explorer.com/z/4P3Pv8r9M.

Решение

Мы можем разбить задачу на две части: поиск циклов и определение размера наибольшего цикла.

Чтобы найти циклы в ориентированном графе, мы можем использовать алгоритм топологической сортировки, оставляющий нам циклы, который работает за O(n), обрабатывая все узлы, не являющиеся частью цикла.

После того, как мы выполнили топологическую сортировку, мы можем пройти каждый оставшийся цикл, подсчитывая количество узлов в этом цикле (также O(n)).

int longest_cycle(std::vector<int64_t>& edges) {
    // Топологическая сортировка
    
    // 1. Подсчет входящих ребер.
    std::vector<int> incoming(edges.size(), 0);
    for (auto v : edges)
        if (v >= 0)
            ++incoming[v];


    // 2. Начинаем с узлов с нулевым количеством
    //    входящих ребер.
    std::queue<int64_t> pending;
    for (int64_t i = 0; i < std::ssize(edges); ++i)
        if (incoming[i] == 0)
            pending.push(i);

    // 3. Обрабатываем до тех пор, пока у нас не будет
    //    необработанных узлов с нулевым количеством
    //    входящих ребер.
    while (!pending.empty()) {
        int64_t idx = pending.front();
        pending.pop();

        // Нет исходящих ребер.
        if (edges[idx] == -1) continue;

        // Удалить это ребро.
        --incoming[edges[idx]];
        // Если мы создали узел с нулевым количеством
        // входящих ребер, добавляем его в очередь.
        if (incoming[edges[idx]] == 0)
            pending.push(edges[idx]);
    }

    // В этой точке, все узлы, не являющиеся частью цикла, 
    // имеют ноль входящих ребер.

    int max = -1;
    // Обходим все циклы:
    for (int64_t i = 0; i < std::ssize(edges); ++i) {
        if (incoming[i] == 0) continue;

        // 1. Это узел в цикле.
        --incoming[i];
        int64_t idx = edges[i];
        int sz = 1;

        // 2. Обходим цикл.
        while (idx != i) {
            --incoming[idx];
            idx = edges[idx];
            ++sz;
        }
        // 3. Отслеживаем самый длинный цикл.
        max = std::max(max, sz);
    }

    return max;
}

Открыть пример на Compiler Explorer.

Теги