Обозначение O-большое: введение для начинающих разработчиков
Обозначение O-большое – один из самых базовых инструментов информатики для анализа временной и пространственной сложности алгоритма.
Выбор алгоритма и структуры данных начинает иметь значение, когда вам нужно написать программное обеспечение со строгими SLA (соглашениями об уровне обслуживания) или для миллионов пользователей.
Обозначение O-большое позволяет сравнивать эффективность различных алгоритмов, поэтому, используя его, когда дело доходит до написания программного обеспечения, вы можете создать хорошо спроектированное и продуманное приложение, которое будет масштабироваться и работать лучше, чем у конкурентов.
Что будет рассмотрено в данной статье:
- Что такое обозначение O-большое?
- Что такое временная и пространственная сложность?
- Распространенные разновидности обозначения O-большое
- Асимптотический анализ: как определить сложность алгоритма
- Примеры кода для обозначений O-большое
- Шпаргалка по обозначению O-большое
Что такое обозначение O-большое?
Обозначение O-большое – это математическая функция, используемая в информатике для описания сложности алгоритма, или, более конкретно, времени выполнения, требуемого алгоритмом. В разработке программного обеспечения оно используется для сравнения эффективности различных подходов к решению задачи.
Используя обозначение O-большое, вы выражаете, насколько быстро растет время выполнения при росте количества входных данных. По сути, это способ понять, насколько масштабируемым является алгоритм.
Это обозначение не сообщает вам, насколько быстро или медленно будет работать алгоритм, но оно сообщает, как изменяется сложность алгоритма в зависимости от размера входных данных.
Что такое временная и пространственная сложность?
Говоря об обозначении O-большое, важно понимать концепции временной и пространственной сложностей, главным образом потому, что обозначение O-большое – это способ классификации сложностей.
Сложность – это приблизительная мера эффективности алгоритма, связанная с каждым написанным вами алгоритмом. Это то, о чем должны знать все программисты.
Есть два вида сложности: временная и пространственная. Временная сложность и пространственная сложность – это, по сути, аппроксимации того, сколько времени и сколько места потребуется алгоритму для обработки определенных входных данных.
Как правило, необходимо определить три уровня (лучший случай, средний случай и худший случай), которые известны как асимптотические обозначения. Эти обозначения позволяют нам ответить на такие вопросы, как:
- Не становится ли алгоритм внезапно невероятно медленным при увеличении размера входных данных?
- Сохраняет ли он быстрое время выполнения при увеличении размера входных данных?
Лучший случай – обозначается как Омега-большое или Ω(n).
Омега-большое (обычно обозначаемая как Ω) представляет собой асимптотическое обозначение для наилучшего случая или минимальную скорость роста для данной функции. Это обозначение дает нам асимптотическую нижнюю границу скорости роста времени выполнения алгоритма.
Средний случай – обозначается как Тета-большое или Θ(n)
Тета (обычно обозначаемая как Θ) является асимптотической записью для обозначения асимптотически жесткой границы скорости роста времени выполнения алгоритма.
Худший случай – обозначается как O-большое или O(n)
O-большое (обычно обозначаемое как O) представляет собой асимптотическое обозначение для наихудшего случая или потолка роста для данной функции. Оно дает нам асимптотическую верхнюю границу скорости роста времени выполнения алгоритма.
Разработчики обычно выбирают наихудший сценарий, O-большое потому, что вы не ожидаете, что ваш алгоритм будет запускаться в лучших или даже средних условиях. Это позволяет вам делать аналитические заявления, такие как «ну, в худшем случае мой алгоритм масштабируется так быстро».
Распространенные разновидности обозначения O-большое
Эти разновидности обозначения O-большое не единственные, но с ними вы, скорее всего, будете сталкиваться часто.
O(1) – постоянная временная сложность
O(1) означает постоянное время выполнения, что означает, что независимо от размера входных данных алгоритм будет иметь одинаковое время выполнения.

Пример:
Массив: вставка или получение элемента
O(log n) – логарифмическая временная сложность
O(log n) означает, что время увеличивается линейно, когда n растет экспоненциально. Таким образом, если для вычисления 10 элементов требуется 1 секунда, то для вычисления 100 элементов потребуется 2 секунды, и так далее. Сложность равна O(log n), когда мы используем алгоритмы «разделяй и властвуй», например, бинарный поиск.

Пример:
Двоичное дерево: вставка или получение элемента
O(n) – линейная временная сложность
O(n) описывает алгоритм, производительность которого будет расти линейно и прямо пропорционально размеру входного набора данных.
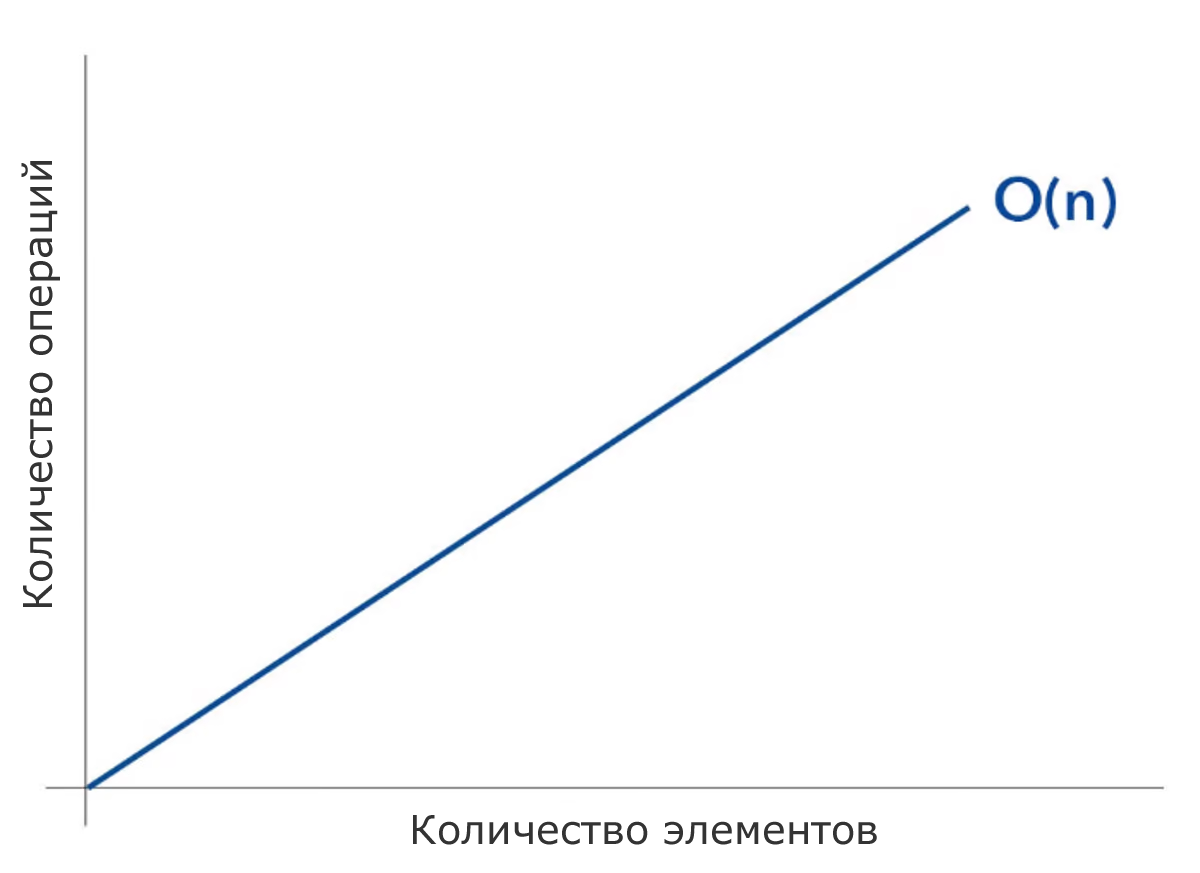
Пример:
Дерево: поиск в глубину (DFS) дерева
O(n²) – квадратичная временная сложность
По мере увеличения количества элементов в вашем списке время, необходимое для работы вашего алгоритма, будет увеличиваться экспоненциально.
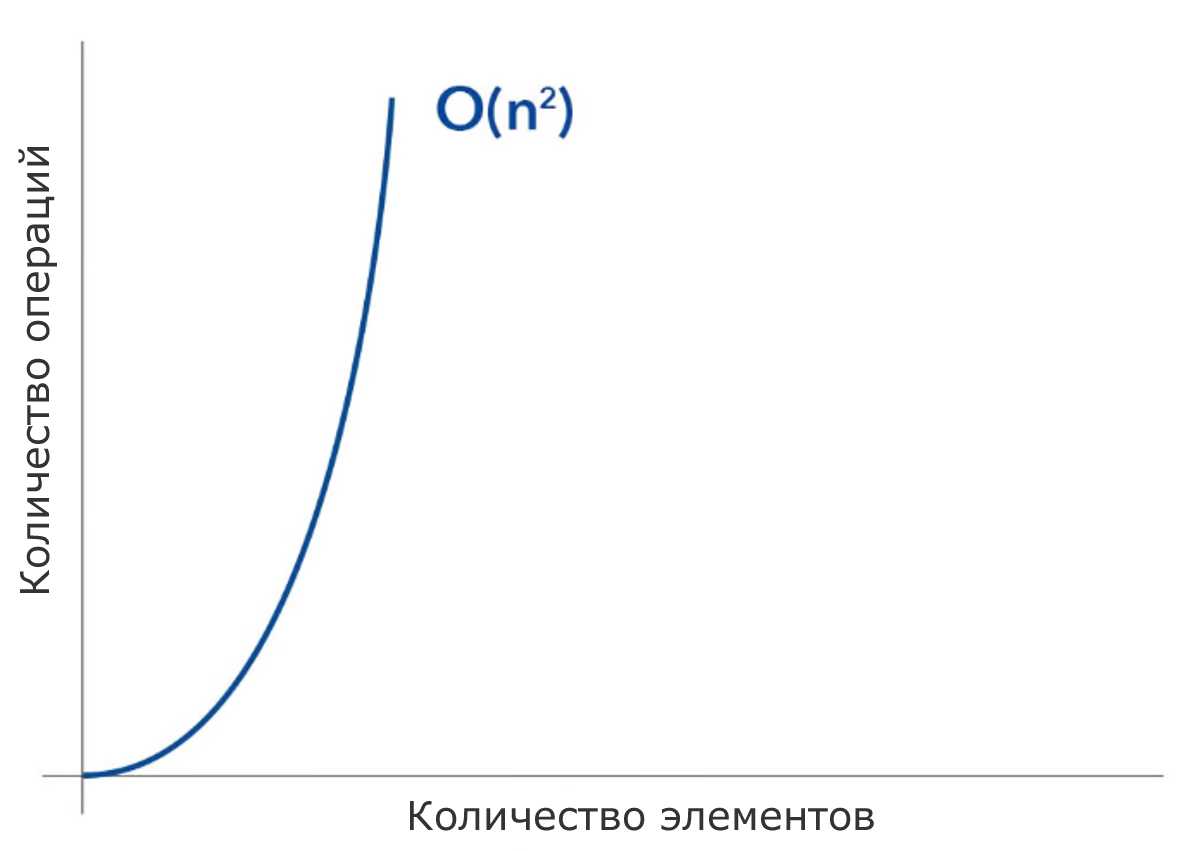
Пример:
Алгоритм сортировки: пузырьковая сортировка и сортировка вставками.
Асимптотический анализ: как определить сложность алгоритма
Как найти O-большое алгоритма
Если на собеседовании вас просят определить сложность O-большое алгоритма, вот общее правило:
- отбросьте ведущие константы;
- игнорируйте члены более низкого порядка.
Пример: найдите сложность O-большое алгоритма с временной сложностью 3n3 + 4n + 2.
Это упрощается до O(n3).
Как найти временную сложность алгоритма
При расчете временной сложности алгоритма вам необходимо выполнить три шага:
- перечислите все основные операции в коде;
- подсчитайте, сколько раз каждая из них была выполнена;
- суммируйте все подсчеты, чтобы получить формулу.
Простой пример, который измеряет временную сложность цикла for размером n:
#include <iostream>
using namespace std;
int main()
{
int n = 10; // O(1)
int sum = 0; // O(1)
for (int i=0; i<n; i++)
sum+=2; // O(1)
cout << sum; // O(1)
return 0;
}
Сначала разделите код на отдельные операции, а затем вычислите, сколько раз они выполняются, что будет выглядеть так:
| Операция | Количество выполнений |
|---|---|
int n = 10; |
1 |
int sum = 0; |
1 |
int i = 0; |
1 |
i < n; |
n + 1 |
i++; |
n |
sum += 2; |
n |
cout << sum; |
1 |
После подсчета количества операций и того, сколько раз каждая операция выполняется, вы просто складываете все эти подсчеты, чтобы получить временную сложность всей программы.
Временная сложность = 1+1+1+(n+1)+n+n+1=3+(n+1)+2n+1=>3n+5
Общие советы по асимптотическому анализу:
- каждый раз, когда список или массив повторяется x раз, сложность, скорее всего, равна O(n);
- когда вы видите задачу, в которой обрабатываемое количество элементов каждый раз уменьшается вдвое, скорее всего, временная сложность будет равна O(log n);
- всякий раз, когда у вас есть единожды вложенный цикл, алгоритм, скорее всего, имеет квадратичную временную сложность.
Полезные формулы для расчета временной сложности алгоритма:
| Суммирование | Формула |
|---|---|
| \[\left( \sum^n_{i=1}c \right) = c + c + c + \cdot \cdot \cdot + c\] | \[cn\] |
| \[\left( \sum^n_{i=1}i \right) = 1 + 2 + 3 + \cdot \cdot \cdot + n\] | \[\frac{n(n+1)}{2}\] |
| \[\left( \sum^n_{i=1}i^2 \right) = 1 + 4 + 9 + \cdot \cdot \cdot + n^2\] | \[\frac{n(n+1)(2n+1)}{6}\] |
| \[\left( \sum^n_{i=0}r^i \right) = r^0 + r^1 + r^2 + \cdot \cdot \cdot + r^n\] | \[\frac{r^{n+1}-1}{r-1}\] |
Примеры кода для обозначений O-большое
О(1)
void printFirstItem(const vector<int>& items)
{
cout << items[0] << endl;
}
Данная функция выполняется за время O(1) (или «постоянное время») относительно своих входных данных. Это означает, что входной массив может состоять из 1 или 1000 элементов, но для данной функции всё равно потребуется всего один «шаг».
О(n)
void printAllItems(const vector<int>& items)
{
for (int item : items) {
cout << item << endl;
}
}
Данная функция выполняется за время O(n) (или «линейное время»), где n – количество элементов в векторе. Если в векторе 10 элементов, необходимо 10 операций печати. Если в нем 1000 элементов, нам придется выполнить 1000 операций печати.
O(n2)
void printAllPossibleOrderedPairs(const vector<int>& items)
{
for (int firstItem : items) {
for (int secondItem : items) {
cout << firstItem << ", " << secondItem << endl;
}
}
}
Здесь у нас два вложенных цикла. Если наш вектор содержит n элементов, наш внешний цикл выполняется n раз, а наш внутренний цикл запускается n раз для каждой итерации внешнего цикла, давая нам общее количество операций печати n2. Таким образом, данная функция выполняется за время O(n2) (или «квадратичное время»). Если в векторе 10 элементов, нам нужно выполнить 100 операций печати. Если в нем 1000 элементов, нам придется выполнить 1000000 операций печати.
Шпаргалка по обозначению O-большое
| Структура данных | Худший случай | Примечания |
|---|---|---|
| Массив | Вставка: O(1) Получение элемента: O(1) |
|
| Связный список | Вставка в конец: O(n) Вставка в начало: O(1) Получение элемента: O(n) |
Обратите внимание, что, если новые элементы добавляются в начало связанного списка, сложность операции вставки становится O(1) |
| Двоичное дерево | Вставка в конец: O(n) Получение элемента: O(n) |
В худшем случае двоичное дерево становится связанным списком. |
| Динамический массив | Вставка: O(1) Получение элемента: O(1) |
Обратите внимание, что при извлечении подразумевается, что мы извлекаем элемент с определенным индексом массива. |
| Стек | Добавление элемента (push): O(1) Удаление элемента (pop): O(1) |
|
| Очередь | Добавление в очередь: O(1) Удаление из очереди: O(1) |
|
| Приоритетная очередь (двоичная куча) | Вставка: O(log n) Удаление: O(log n) Получение min/max: O(1) |
|
| Хеш-таблица | Вставка: O(n) Получение: O(n) |
Помните, что средний случай вставки и извлечения из хеш-таблицы – O(1) |
| B-деревья | Вставка: O(log n) Получение: O(log n) |
|
| Красно-черные деревья | Вставка: O(log n) Получение: O(log n) |
| Алгоритм | Худший случай | Примечания |
|---|---|---|
| Алгоритмы сортировки/поиска | Пузырьковая сортировка: O(n2) Сортировка вставками: O(n2) Сортировка выбором: O(n2) Быстрая сортировка: O(n2) Сортировка слиянием: O(log n) |
Обратите внимание, хотя производительность быстрой сортировки в худшем случае составляет O(n2), но на практике она используется часто, поскольку ее средний случай - O(n log n). |
| Алгоритмы работы с деревьями | Поиск в глубину: O(n) Поиск в ширину: O(n) Прямой, центрированный и обратный обходы: O(n) |
n – общее количество узлов в дереве. Большинство алгоритмов обхода дерева в конечном итоге просматривает каждый узел в дереве, и их сложность в худшем случае, таким образом, составляет O(n). |
