Цифровая модуляция: амплитуда и частота

Хотя и основанные на одних и тех же концепциях, сигналы с цифровой модуляцией сильно отличаются от аналоговых коллег.

Аналоговая модуляция, хотя далеко и не вымерла, но она просто несовместима с цифровым миром. Мы больше не фокусируем наши усилия на перемещении аналоговых сигналов из одного места в другое. Скорее мы хотим перемещать цифровые данные: беспроводная сеть, оцифрованные аудиосигналы, показания датчиков и так далее. Для передачи цифровых данных используется цифровая модуляция.

Однако мы должны быть осторожны с этой терминологией. «Аналоговый» и «цифровой» в этом контексте относятся к типу передаваемой информации, а не к основным характеристикам фактически передаваемых сигналов. И аналоговая, и цифровая модуляции используют плавно изменяющиеся сигналы; разница заключается в том, что аналого-модулированный сигнал демодулируется в аналоговый низкочастотный сигнал, тогда как цифровой модулированный сигнал состоит из дискретных единиц модуляции, называемых символами, которые интерпретируются как цифровые данные.

Существуют аналоговые и цифровые версии трех типов модуляции. Давайте начнем с амплитуды и частоты.

Цифровая амплитудная модуляция

Это тип модуляции называется амплитудной манипуляцией (ASK, amplitude shift keying). Самый простой случай «включение-выключение» (OOK, on-off keying), и это почти соответствует математическим связям, обсуждаемым на странице, посвященной «аналоговой амплитудной модуляции»: если мы используем цифровой сигнал в качестве низкочастотного модулирующего сигнала, то перемножение модулирующего сигнала и несущей приводит к модулированному сигналу, который идет с нормальным уровнем при высоком логическом уровне и «выключен» при низком логическом уровне. Амплитуда логической единицы соответствует индексу модуляции.

Временная область

Следующий график показывает сигнал амплитудной манипуляции «включено-выключено», сгенерированный с использованием несущей 10 МГц и цифрового тактового сигнала 1 МГц. Здесь мы работаем в математической области, поэтому амплитуда логической единицы (и амплитуда несущей) просто безразмерная «1», в реальной схеме вы можете иметь несущую с амплитудой 1 вольт и логический сигнал 3,3 вольта.

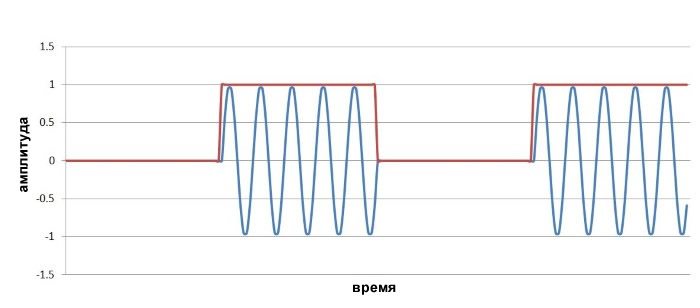
Возможно, вы заметили одно несоответствие между этим примером и математическими отношениями, обсуждавшимися на странице «Амплитудная модуляция»: мы не сдвинули низкочастотный модулирующий сигнал. Если вы имеете дело с типовым цифровым сигналом, в котором присутствует постоянная составляющая, то смещение вверх не требуется, поскольку сигнал всегда остается на положительном участке оси y.

Частотная область

Ниже показан соответствующий спектр:

Сравните его со спектром сигнала, модулированного по амплитуде с использованием сигнала синусоиды 1 МГц:

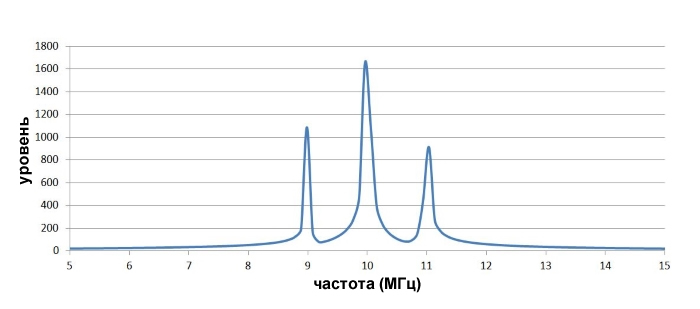
Бо́льшая часть спектра одинакова: пик на несущей частоте (f_нес), пик на f_нес плюс частота модулирующего сигнала и пик на f_нес минус частота модулирующего сигнала. Однако спектр амплитудной манипуляции имеет меньшие пики, соответствующие 3-й и 5-й гармоникам: основная частота (f_F) равна 1 МГц, что означает, что 3-я гармоника (f₃) равна 3 МГц, а 5-я гармоника (f₅) равна 5 МГц. Таким образом, у нас есть пики при f_нес плюс/минус f_F, f₃ и f₅. И на самом деле, если бы вы расширили график, то увидели бы, что пики продолжают появляться в соответствии с этим примером.

Это имеет смысл. Преобразование Фурье прямоугольного сигнала состоит из синусоидальной волны на основной частоте и нечетных гармоник с понижающимися амплитудами, и эти гармонические составляющие являются тем, что мы видим на спектре, показанном выше.

Это обсуждение приводит нас к важной практической точке: резкие переходы, связанные с цифровыми методами модуляции, создают (нежелательные) высокочастотные составляющие. Мы должны помнить об этом, когда рассматриваем фактическую ширину полосы частот модулированного сигнала и наличие частот, которые могут мешать другим устройствам.

Цифровая частотная модуляция

Этот тип модуляции называется частотной манипуляцией (FSK, frequency shift keying). Для наших целей нет необходимости рассматривать математическое выражение частотной манипуляции; скорее мы просто можем указать, что будем иметь частоту f₁, когда модулирующие данные равны логическому 0, и частоту f₂, когда модулирующие данные равны логической 1.

Временная область

Одним из способов генерации готового для передачи FSK сигнала является сначала создание аналогового низкочастотного сигнала, который переключается между f₁ и f₂ в соответствии с цифровыми данными. Ниже приведен пример низкочастотного FSK сигнала с f₁ = 1 кГц и f₂ = 3 кГц. Чтобы гарантировать, что символ имеет одинаковую продолжительность и для логического 0, и для логической 1, мы используем один период для 1 кГц и три периода для 3 кГц.

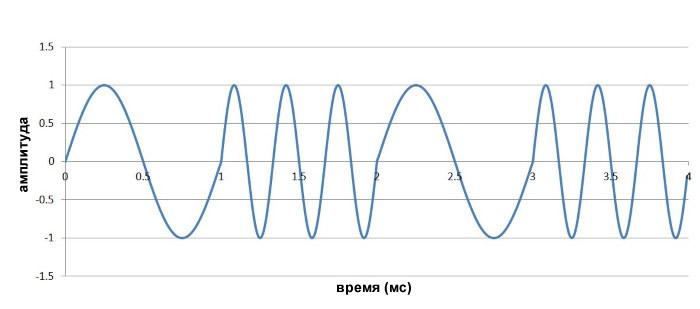
Затем низкочастотный сигнал сдвигается (используя смеситель) до несущей частоты и передается. Этот подход особенно удобен в программных радиосистемах: аналоговый модулирующий сигнал является низкочастотным, и поэтому он может быть сгенерирован математически, а затем введен в аналоговую область с помощью ЦАП. Использование ЦАП для высокочастотного передаваемого сигнала было бы намного сложнее.

Более простой способ реализации FSK состоит в том, чтобы просто иметь два сигнала несущей с разными частотами (f₁ и f₂); и тот или иной сигнал подается на выход в зависимости от логического уровня двоичных данных. Это приводит к конечному передаваемому сигналу, который резко переключается между двумя частотами, так же, как низкочастотный FSK сигнал, за исключением того, что разница между двумя частотами здесь намного меньше по сравнению со средней частотой. Другими словами, если бы вы смотрели на график во временной области, было бы сложно визуально различить участки с f₁ от участков с f₂, потому что разница между f₁ и f₂ является лишь крошечной долей f₁ (или f₂).

Частотная область

Давайте посмотрим на результат частотной манипуляции в частотной области. В этом случае мы будем использовать ту же несущую частоту 10 МГц (или, в этом случае, среднюю частоту), и будем использовать ±1 МГц в качестве отклонения (это не реальный пример, но удобный для наших целей). Таким образом, передаваемый сигнал будет 9 МГц для логического 0 и 11 МГц для логической 1. Ниже показан спектр полученного сигнала:

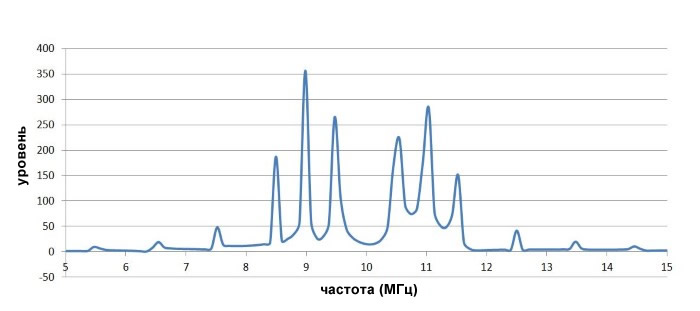
Обратите внимание, что на «несущей частоте» нет энергии. Это неудивительно, учитывая, что модулированный сигнал никогда не находится на частоте 10 МГц. Он всегда находится на частоте 10 МГц минус 1 МГц или 10 МГц плюс 1 МГц, и именно там мы видим два доминирующих всплеска: 9 МГц и 11 МГц.

Но что насчет других частот, присутствующих в этом спектре? Ну, спектральный анализ FSK не особенно прост. Мы знаем, что будет добавлена дополнительная энергия Фурье, связанная с резкими переходами между частотами. Оказывается, что FSK приводит к sinc-функциональному типу спектра для каждой частоты, то есть один центрирован на f₁, а другой центрирован на f₂. Они учитывают дополнительные частотные всплески по обе стороны от двух доминирующих пиков.

Резюме

• Цифровая амплитудная модуляция включает в себя изменение амплитуды несущей волны в дискретных участках в соответствии с двоичными данными.
• Самый простой подход к цифровой амплитудной модуляции – это «включение-выключение».
• При цифровой частотной модуляции частота несущей или низкочастотного аналогового сигнала изменяется в дискретных участках в соответствии с двоичными данными.
• Если сравнить цифровую модуляцию с аналоговой, мы увидим, что резкие переходы, создаваемые цифровой модуляцией, приводят к появлению энергии на дополнительных частотах, расположенных дальше от несущей.

Теги