Фазовая модуляция: теория, временная и частотная области

Фазовая модуляция (ФМ, англ. PM) похожа на частотную модуляцию и является важной технологией в цифровых системах связи.

Все мы слышали об AM радио и FM радио. Но фазовая модуляция, видимо, относится к другой категории – «PM радио» ни в коем случае не является распространенным термином. Оказывается, что фазовая модуляция более актуальна в контексте цифровой радиосвязи. Тем не менее, мы можем сказать, что PM радио так же распространено, как FM радио, просто потому, что между фазовой модуляцией и частотной модуляцией мало различий. ЧМ и ФМ лучше всего рассматривать как два тесно связанных варианта угловой модуляции, где «угол» относится к модификации величины, передаваемой функции синуса или косинуса.

Математика

В предыдущей статье мы видели, что частотная модуляция достигается путем добавления интеграла низкочастотного модулирующего сигнала к аргументу функции синуса или косинуса (где функция синуса или косинуса представляет собой сигнал несущей):

\[x_{чм}(t)=\sin \left( \omega_{нес}t+\int_{-\infty}^{t} x_{нч}(t)dt \right) \]

Однако вы вспомните, что мы перешли к частотной модуляции, сначала обсуждая фазовую модуляцию: добавление самого низкочастотного модулирующего сигнала, а не его интеграла, заставляет фазу меняться в соответствии с амплитудой модулирующего сигнала. Таким образом, фазовая модуляция на самом деле немного проще частотной.

\[x_{фм}(t)=\sin \left( \omega_{нес}t+x_{нч}(t) \right) \]

Как и в случае частотной модуляции, мы можем использовать индекс модуляции, чтобы сделать изменения фазы более чувствительными к изменениям амплитуды низкочастотного модулирующего сигнала:

\[x_{фм}(t)=\sin \left( \omega_{нес}t+mx_{нч}(t) \right) \]

Сходство между фазовой и частотной модуляциями становится более явным, если мы рассмотрим низкочастотный модулирующий сигнал, состоящий из одной частоты. Предположим, что x_нч(t) = sin(ω_нчt). Интеграл синуса равен отрицательному косинусу (плюс константа, которую мы можем здесь игнорировать) – другими словами, интеграл представляет собой просто сдвинутую по времени версию исходного сигнала. Таким образом, если мы выполняем фазовую модуляцию и частотную модуляцию с помощью этого низкочастотного модулирующего сигнала, единственной разницей в модулированных сигналах будет выравнивание между амплитудой низкочастотного модулирующего сигнала и изменениями в сигнале несущей; сами изменения будут одинаковы. Это будет понятно в следующем разделе, где мы рассмотрим некоторые временны́е графики.

Важно иметь в виду, что мы имеем дело с мгновенной фазой, так же как частотная модуляция основана на концепции мгновенной частоты. Термин «фаза» довольно расплывчатый. Одно знакомое значение относится к начальному состоянию синусоиды; например «обычная» синусоида начинается со значения нуля и затем увеличивается в сторону своего максимального значения. Синусоида, которая начинается в другой точке своего периода, имеет сдвиг фазы. Мы можем также думать о фазе как о конкретной части полного периода сигнала, например, в фазе π/2 синусоида завершила одну четверть своего периода.

Эти интерпретации «фазы» нам не очень помогают, когда мы имеем дело с фазой, которая постоянно изменяется в зависимости от формы низкочастотного модулирующего сигнала. Скорее мы используем концепцию мгновенной фазы, т.е. фазы в заданный момент времени, которая соответствует значению, переданному (в заданный момент) тригонометрической функции. Мы можем думать об этих непрерывных изменениях в мгновенной фазе как о «толкании» значения несущей дальше или ближе к предыдущему состоянию формы волны.

Еще одна вещь, о которой нужно помнить: тригонометрические функции, включая синус и косинус, работают с углами. Изменение аргумента тригонометрической функции эквивалентно изменению угла, а это объясняет, почему и частотная, и фазовая модуляции описываются как угловая модуляция.

Временна́я область

Мы будем использовать те же сигналы, которые использовали при обсуждении FM, то есть несущую 10 МГц и низкочастотный модулирующий сигнал синусоиды 1 МГц:

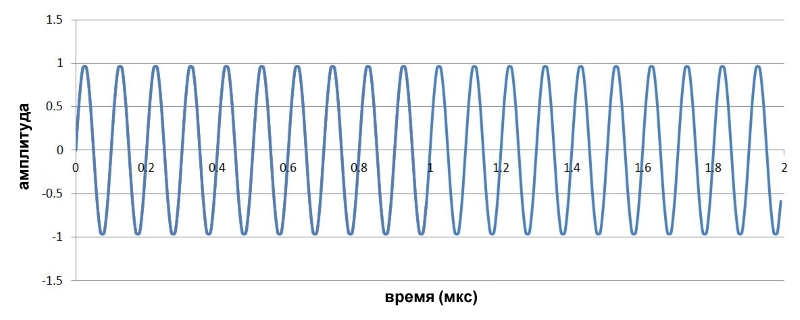
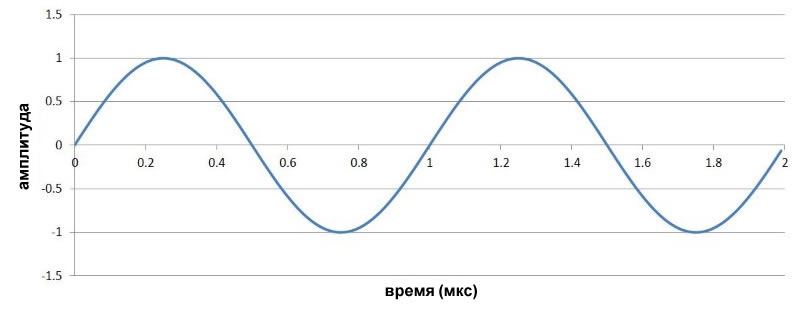
Ниже показан частотно-модулированный сигнал (с m=4), который мы видели в предыдущей статье:

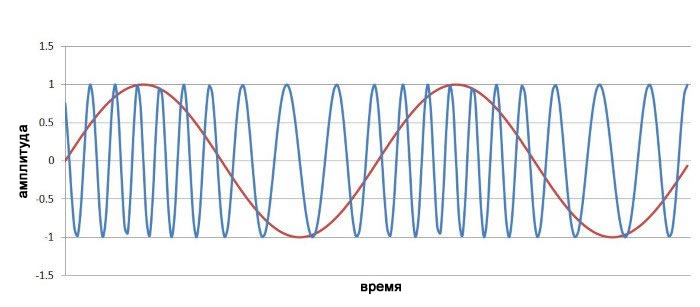
Мы можем рассчитать форму волны фазомодулированного сигнала, используя следующую формулу, где сигнал, добавленный к аргументу волны сигнала несущей, использует положительный синус (т.е. исходный сигнал) вместо отрицательного косинуса (т.е. интеграла исходного сигнала).

\[ x_{фм}(t)=\sin \left( (10\times10^6\times2\pi t)+\sin(1\times10^6\times2\pi t) \right) \]

Ниже показан график сигнала с фазовой модуляцией:

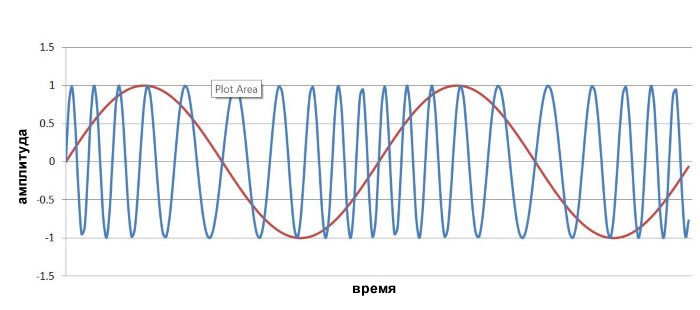
Прежде чем обсудить его, давайте посмотрим на диаграмму, которая одновременно показывает формы частотно-модулированного сигнала и фазомодулированного сигнала:

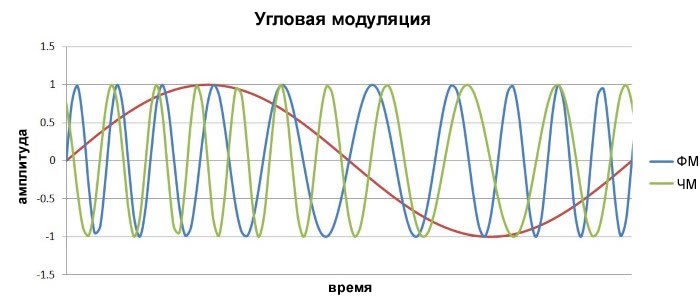
Первое, что здесь приходит в голову, это то, что с визуальной точки зрения частотная модуляция более интуитивно понятна по сравнению с фазовой модуляцией; существует четкая визуальная связь между участками с более высокой и низкой частотой и более высокими и более низкими уровнями низкочастотного модулирующего сигнала. В фазовой модуляции связь между низкочастотным модулирующим сигналом и поведением несущей, возможно, не сразу очевидна. Однако после небольшого осмотра мы видим, что частота несущей в фазовой модуляции соответствует наклону формы волны модулирующего сигнала, наиболее высокочастотные участки соответствуют времени самого крутого положительного наклона x_нч, а наиболее низкочастотные участки соответствуют времени самого крутого отрицательного наклона.

Это имеет смысл. Напомним, что частота (как функция времени) является производно фазы (как функции времени). При фазовой модуляции наклон формы низкочастотного модулирующего сигнала определяет, как быстро изменяется фаза, и скорость изменения фазы эквивалентна частоте. Поэтому в фазомодулированном сигнале высокий наклон модулирующего сигнала соответствует высокой частоте, а низкий наклон модулирующего сигнала соответствует низкой частоте. В частотной модуляции мы используем интеграл от x_нч, который приводит к сдвигу высокочастотных (или низкочастотных) участков несущей к значениям модулирующего сигнала, следующих после высоких (или низких) наклонных участков формы низкочастотного модулирующего сигнала.

Частотная область

Предыдущие графики во временной области демонстрируют сказанное ранее: частотная модуляция и фазовая модуляция очень похожи. Поэтому неудивительно, что эффект от фазовой модуляции в частотной области аналогичен эффекту от частотной модуляции. Ниже представлены спектры сигналов с фазовой модуляцией с использованием сигнала несущей и низкочастотного модулирующего сигнала, используемых выше:

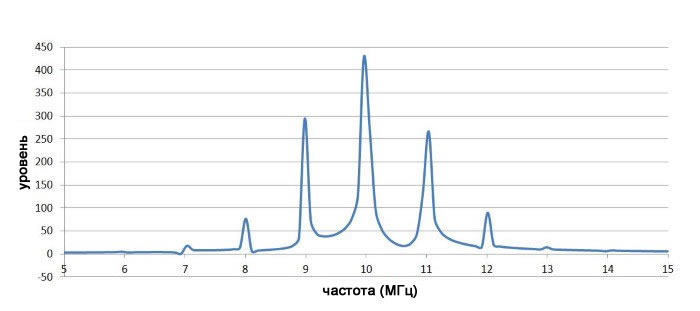
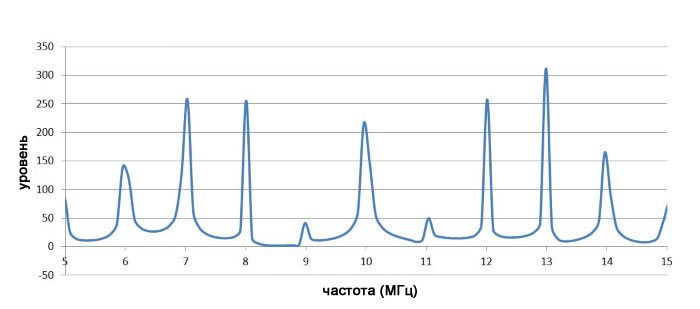
Резюме

• Фазовая модуляция рассчитывается путем добавления низкочастотного модулирующего сигнала к аргументу функции синуса или косинуса, которая представляет собой сигнал несущей.
• Индекс модуляции делает изменения фазы более или менее чувствительными к поведению модулирующего сигнала.
• Эффекты от фазовой модуляции в частотной области похожи на эффекты от частотной модуляции.
• Аналоговая фазовая модуляция не распространена, однако цифровая фазовая модуляция используется широко.

Теги