Децибелы
В простейшем виде, коэффициент усиления усилителя – это отношение выхода к входу. Как и все коэффициенты, коэффициент усиления безразмерен. Тем не менее, существует реальная единица измерения, предназначенная для представления коэффициента усиления, и называется она бел.
Как единица измерения, бел фактически был придуман для удобства представления потерь мощности в системе телефонных проводов, а не для коэффициента усиления усилителей. Название единицы измерения происходит от Александра Грэма Белла, известного шотландского изобретателя, чья работа сыграла важную роль в развитии телефонных систем. Первоначально, бел выражал количество потерь мощности сигнала в электрическом кабеле стандартной длины из-за его сопротивления. Теперь же он является общим термином для обозначения логарифма (с основанием 10) отношения мощностей (выходной мощности, деленной на входную мощность):
\[A_{P(раз)} = \frac{P_{вых}}{P_{вх}}\]
\[A_{P(Бел)} = \log \frac{P_{вых}}{P_{вх}}\]
Поскольку бел является логарифмической единицей, он нелинеен. Чтобы дать вам представление о том, как это работает, рассмотрим следующую таблицу значений, сравнивая потери и усиления по мощности в децибелах с безразмерными коэффициентами:;
| Усиление/потери в разах | Усиление/потери в белах |
|---|---|
| \[ \frac{P_{вых}}{P_{вх}}\] | \[ \log \frac{P_{вых}}{P_{вх}}\] |
| 1000 | 3 Б |
| 100 | 2 Б |
| 10 | 1 Б |
| 1 (нет потерь или усиления) | 0 Б |
| 0,1 | – 1 Б |
| 0,01 | – 2 Б |
| 0,001 | – 3 Б |
| 0,0001 | – 4 Б |
Позже было решено, что бел был слишком большой единицей измерения, чтобы пользоваться им напрямую, и поэтому он стал применяться с метрической приставкой деци (что означает 1/10), что дает децибелы или дБ (dB). Сейчас выражение «дБ» встречается настолько часто, что многие люди не понимают, что это сочетание «деци-» и «-бел», или что даже есть такая единица измерения, как «бел». Чтобы представить это, вот еще одна таблица сравнения усиления/потерь в разах и децибелах:
| Усиление/потери в разах | Усиление/потери в децибелах |
|---|---|
| \[ \frac{P_{вых}}{P_{вх}}\] | \[ 10 \, \log \frac{P_{вых}}{P_{вх}}\] |
| 1000 | 30 дБ |
| 100 | 20 дБ |
| 10 | 10 дБ |
| 1 (нет потерь или усиления) | 0 дБ |
| 0,1 | – 10 дБ |
| 0,01 | – 20 дБ |
| 0,001 | – 30 дБ |
| 0,0001 | – 40 дБ |
Как логарифмическая единица измерения, этот способ измерения коэффициента усиления охватывает широкий диапазон отношений с минимальным диапазоном чисел. Разумно спросить, «почему кто-то решил, что необходимо придумать логарифмическую единицу измерения потерь мощности электрического сигнала в телефонной системе?». Ответ связан с динамикой человеческого слуха, сила восприимчивости которого имеет логарифмическую природу.
Человеческий слух крайне нелинеен: для того, чтобы удвоить воспринимаемую громкость звука, фактическая мощность звука должна быть умножена в 10 раз. Относительно потерь мощности телефонного сигнала логарифмическая шкала в «белах» идеально подходит по смыслу в данном контексте: потери мощности на 1 бел соответствуют потерям воспринимаемого звука на 50 процентов, или на 1/2. Усиление мощности на 1 бел соответствует удвоению воспринимаемой громкости звука.
Почти полной аналогией шкалы в белах является шкала Рихтера, используемая для описания силы землетрясения: землетрясение 6,0 баллов по шкале Рихтера в 10 раз мощнее, чем землетрясение 5,0 баллов; землетрясение 7,0 баллов по шкале Рихтера в 100 раз мощнее, чем землетрясение 5,0 баллов, и так далее. Шкала измерения химического показателя pH также логарифмическая, разница в 1 по шкале эквивалентна десятикратной разнице в концентрации ионов водорода в химическом растворе. Преимущество использования логарифмической шкалы измерения заключается в выражении огромного диапазона значений, обеспечиваемом относительно небольшим диапазоном числовых значений, и это же преимущество позволяет использовать баллы Рихтера для землетрясений и pH для активности ионов водорода.
Еще одна причина для использования белов, как единицы измерения коэффициента усиления, – это простота формул коэффициентов усиления и потерь. Рассмотрим последний пример (рисунок на предыдущей странице), где два усилителя подключены друг к другу для усиления сигнала. Соответствующий коэффициент усиления для каждого усилителя был выражен в разах, а общий коэффициент усиления системы был равен произведению этих двух коэффициентов:
Общий коэффициент усиления = 3 x 5 = 15Если эти цифры представляют собой коэффициенты усиления по мощности, мы можем непосредственно применить единицы измерения в белах, чтобы выразить коэффициент усиления каждого усилителя и системы в целом (рисунок ниже).
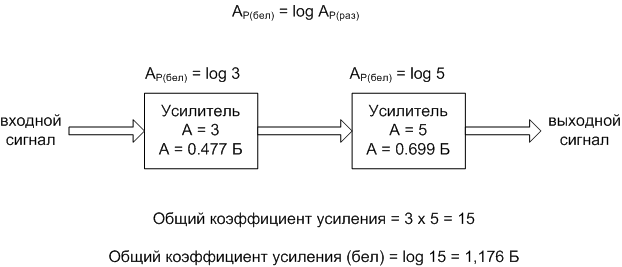
При близком рассмотрении значений этих коэффициентов усиления в единицах «бел» можно заметить: они складываются. Значения коэффициентов усиления в разах для каскадов усилителей перемножаются, а значения коэффициентов усиления в белах складываются для получения общего коэффициента усиления системы. Первый усилитель с коэффициентом усиления по мощности 0,477 Б добавляется к коэффициенту усиления по мощности второго усилителя 0,699 Б, чтобы получить общий коэффициент усиления системы 1,176 Б.
При пересчете в децибелах мы видим то же самое (рисунок ниже).
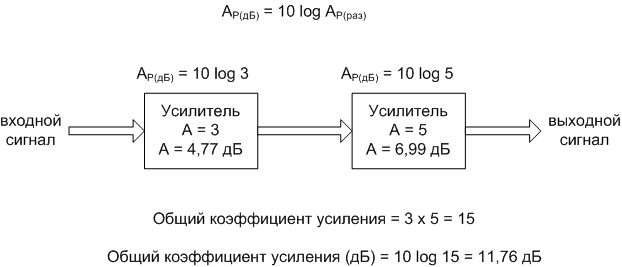
Для тех, кто уже знаком с математическими свойствами логарифмов, это не было сюрпризом. Это элементарное правило алгебры: антилогарифм суммы значений логарифмов двух чисел равен произведению этих двух чисел. Другими словами, если мы возьмем два числа и определим логарифм каждого из них, затем сложим значения двух логарифмов вместе, а затем определим «антилогарифм» этой суммы (возвести основание логарифма - в данном случае 10 - в степень этой суммы), результат будет таким же, как если бы мы просто перемножили два изначальных числа. Это алгебраическое правило формирует суть устройства, называемого логарифмической линейкой, аналоговым компьютером, который, помимо прочего, может определять произведения и частные от деления с помощью сложения (сложение физических длин, отмеченных на движущихся деревянных, металлических или пластиковых шкалах). При наличии таблицы значений логарифмов, этот же математический трюк может быть использован для выполнения другим способом сложных умножений и делений с помощью только сложений и вычитаний соответственно. С появлением высокоскоростных микрокалькуляторов, эта элегантная технология расчетов практически исчезла из популярного использования. Тем не менее, это всё еще важно понимать при работе с измерительными шкалами, которые являются логарифмическими, такими, как бел (децибел) и шкала Рихтера.
При преобразовании коэффициента усиления по мощности из бел или децибел в безразмерные коэффициенты, используется обратная математическая функция для логарифмирования: возведение числа 10 в степень или антилогарифм.
Если
\[A_{P(Бел)} = \log A_{P(раз)}\]
то
\[A_{P(раз)} = 10^{A_{P(Бел)}}\]
Преобразование децибел в безразмерные коэффициенты для коэффициентов усиления по мощности почты такое же, только в показатель степени добавляется делитель на 10:
Если
\[A_{P(дБ)} = 10 \, \log A_{P(раз)}\]
то
\[A_{P(раз)} = 10^{\frac{A_{P(дБ)}}{10}}\]
Пример:
Мощность на входе усилителя составляет 1 Ватт, а мощность на выходе – 10 Ватт. Найдите коэффициент усиления в дБ.
\[A_{P(дБ)} = 10 \, \log_{10} (P_{вых}/P_{вх}) = 10 \, \log_{10} (10/1) = 10 \, (1) = 10 \, дБ\]
Пример:
Найдите коэффициент усиления по мощности AP(раз) = (Pвых/Pвх) для коэффициента усиления по мощности 20 дБ.
\[A_{P(дБ)} = 20 = 10 \, \log_{10} A_{P(раз)}\]
\[20/10 = \log_{10} A_{P(раз)}\]
\[10^{20/10} = 10^{\log_{10} A_{P(раз)}}\]
\[100 = A_{P(раз)} = (P_{вых}/P_{вх})\]
Поскольку бел изначально является единицей измерения усиления или потерь мощности в системе, усиление и потери по напряжению или по току не могут быть преобразованы в белы или децибелы совсем таким же способом. При использовании бел или децибел для выражения усиления других величин, кроме мощности, будь то напряжение или ток, мы должны выполнить расчет, какой коэффициент усиления по мощности соответствует заданному коэффициенту усиления по напряжению или току. Для постоянного сопротивления нагрузки, усиление напряжения или тока в 2 раза соответствует усилению по мощности в 4 раза (22); усиление напряжения или тока в 3 раза соответствует усилению по мощности в 9 раз (32). Если мы умножим напряжение или ток на какой-либо коэффициент, то усиление по мощности будет равно квадрату этого коэффициента. Это связано с формулами закона Джоуля–Ленца, где мощность рассчитывалась из значений напряжения или тока и сопротивления:
\[P = \frac{U^2}{R}\]
\[P = I^2R\]
Мощность пропорциональна и квадрату напряжения, и квадрату тока.
Таким образом, при переводе коэффициента усиления по напряжению или току из раз в белы, мы должны включить этот показатель степени в уравнения:
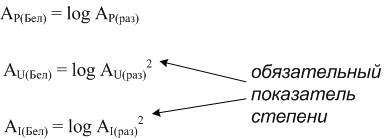
Такой же показатель степени необходим и выражении коэффициента усиления по току или напряжению и в децибелах:
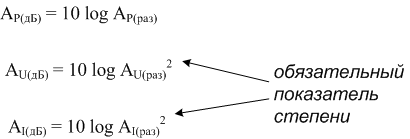
Тем не менее, благодаря еще одному интересному свойству логарифмов, мы можем упростить эти уравнения, устранив показатель степени и добавив «2», как множитель к функции логарифма. Другими словами, вместо вычисления логарифма квадрата напряжения или тока, мы просто умножаем значение логарифма коэффициента усиления напряжения или тока на 2, окончательный результат в белах или децибелах будет точно таким же:
для бел:
для децибел:
Процесс преобразования коэффициентов усиления по напряжению или току из бел или децибел в безразмерные коэффициенты почты точно такой же, как и для коэффициентов усиления по мощности:
И уравнения, используемые для преобразования коэффициентов усиления по напряжению или току в децибелах в безразмерные коэффициенты:
В то время как бел – это единица, изначально сопоставимая с мощностью, другая логарифмическая единица, придуманная, чтобы выразить усиление/потери по напряжению или току, основывается на натуральном логарифме, а не на десятичном, как белы и децибелы. Названная непером, единица измерения обозначается «Нп» («Np», может встречаться и с «n» в нижнем регистре).
К лучшему или к худшему, ни непер, ни его ослабленный кузен, децинепер, не очень широко используются в качестве единицы измерений в американских инженерных приложениях.
Пример:
Напряжение на линейном 600 омном входе усилителя составляет 10 мВ, напряжение на его нагрузке 600 Ом составляет 1 В. Найдите коэффициент усиления по мощности в дБ.
\[A_{дБ} = 20 \, \log_{10}(U_{вых} / U_{вх}) = 20 \, \log_{10}(1/0.01) = 20 \, \log_{10}(100) = 20 (2) = 40 \, дБ\]
Пример:
Найти коэффициент усиления по напряжению в разах AU(раз) = (Uвых/Uвх) для усилителя с коэффициентом усиления 20 дБ и входным и выходным сопротивлениями, равными 50 Ом.
\[A_{U(дБ)} = 20 \, \log_{10}A_{U(раз)}\]
\[20 = 20 \, \log_{10}A_{U(раз)}\]
\[20/20 = \log_{10}A_{U(раз)}\]
\[10^{20/20} = 10^{\log_{10}A_{U(раз)}}\]
\[10= A_{U(раз)} = (U_{вых}/U_{вх})\]
Подведем итоги:
Усиление и потери могут быть выражены в безразмерных коэффициентах или в единицах измерения белах (Б) или децибелах (дБ). Децибел – это буквально деци-бел: одна десятая часть бела.
Бел – единица изначально для выражения усиления или потерь по мощности. Чтобы преобразовать отношение мощностей в белы или децибелы, используйте одно из этих уравнений:
При использовании единицы измерения бел или децибел для выражения отношений напряжений или токов, необходимо основываться на эквивалентном отношении мощностей. Практически это означает использование других уравнений с коэффициентом умножения 2 для значений логарифмов, что соответствует степени 2 в отношениях напряжений или токов:
Чтобы преобразовать усиление в децибелах в безразмерный коэффициент усиления, используйте одно из этих уравнений:
\[A_{U(раз)} = 10^{\frac{A_{U(дБ)}}{20}}\]
\[A_{I(раз)} = 10^{\frac{A_{I(дБ)}}{20}}\]
\[A_{P(раз)} = 10^{\frac{A_{P(дБ)}}{10}}\]
Усиление (увеличение) выражается в положительных значениях бел или децибел. Потери (затухание) выражаются в отрицательных значениях бел или децибел. Единичное усиление (нет ни усиления, ни потерь; отношение = 1) выражается, как ноль бел или ноль децибел.
При расчете общего коэффициента усиления для усилительной системы, состоящей из нескольких каскадов усилителей, отдельные коэффициенты усиления в разах перемножаются, чтобы найти общий коэффициент усиления в разах. Значения бел и децибел для каждого усилительного каскада, с другой стороны, суммируются для определения общего коэффициента усиления в белах или децибелах.
