Диаграмма Смита
Диаграмма Смита – это один из наиболее полезных графических инструментов для расчета высокочастотных схем. Диаграмма обеспечивает удобный способ визуализации сложных функций, и она продолжает пользоваться популярностью спустя десятилетия после появления ее первой концепции.
С математической точки зрения диаграмма Смита представляет собой четырехмерное представление всех возможных комплексных импедансов относительно координат, определяемых комплексным коэффициентом отражения.
Область определения коэффициента отражения для линии без потерь представляет собой окружность единичного радиуса в комплексной плоскости. Это также является областью диаграммы Смита.
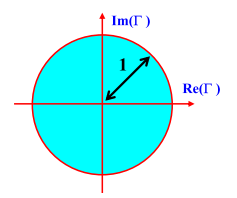
Назначение диаграммы Смита заключается в том, чтобы идентифицировать все возможные импедансы в области существования коэффициента отражения. Для этого мы исходим из общего определения импеданса линии (что в равной степени применимо к импедансу нагрузки при d=0).
\[Z(d) = { V(d) \over I(d) } = Z_0 { 1 + \Gamma(d) \over 1 - \Gamma(d) }\]
Это обеспечивает комплексную функцию \(Z(d) = f\{\text{Re}(\Gamma), \text{Im} (\Gamma)\}\), которую мы хотим отобразить на графике. Очевидно, что результат применим только к линиям с импедансом, точно равным Z0.
Чтобы получить универсальные кривые, мы введем понятие нормированного импеданса:
\[z_n(d) = { Z(d) \over Z_0 } = { 1 + \Gamma(d) \over 1 - \Gamma(d) }\]
Нормализированный импеданс представлен на диаграмме Смита с использованием семейств кривых, которые идентифицируют нормализированное активное сопротивление r (действительная часть) и нормализованное реактивное сопротивление x (мнимая часть).
\[z_n(d) = \text{Re}(z_n) + j \text{Im}(z_n) = r + jx\]
Представим коэффициент отражения через его координаты.
\[\Gamma(d) = \text{Re}(\Gamma) + j\text{Im}(\Gamma)\]
Теперь мы можем записать
\[r+jx = { 1 + \text{Re}(\Gamma) + j\text{Im}(\Gamma) \over 1 - \text{Re}(\Gamma) - j\text{Im}(\Gamma) } = { 1 - \text{Re}^2(\Gamma) - \text{Im}^2(\Gamma) + j2\text{Im}(\Gamma) \over (1 - \text{Re}(\Gamma))^2 + \text{Im}^2(\Gamma) }\]
Действительная часть дает
\[r = { 1 - \text{Re}^2(\Gamma) - \text{Im}^2(\Gamma) \over (1 - \text{Re}(\Gamma))^2 + \text{Im}^2(\Gamma) }\]
\[r \left( \text{Re}(\Gamma) - 1 \right)^2 + \left(\text{Re}^2(\Gamma) - 1 \right) +r \text{Im}^2(\Gamma) + \text{Im}^2(\Gamma) + \overbrace{ {1\over 1 + r} - {1 \over 1 +r} }^{=0} = 0 \; \left( \begin{matrix} \text{добавляем значение,} \\ \text{равное нулю} \end{matrix} \right) \]
\[\left[ r (\text{Re}(\Gamma) - 1)^2 + \left( \text{Re}^2(\Gamma) - 1 \right) + {1 \over 1 +r} \right] + (1 +r) \text{Im}^2(\Gamma) = { 1 \over 1 +r }\]
\[(1 +r) \left[ \text{Re}^2(\Gamma) - 2\text{Re}(\Gamma){1 \over 1 +r} + { r^2 \over (1 + r)^2} \right] + (1 +r)\text{Im}^2(\Gamma) = {1 \over 1 +r}\]
\[\left[ \text{Re}(\Gamma) - {r \over 1 +r} \right]^2 + \text{Im}^2(\Gamma) = \left( {1 \over 1 +r} \right)^2 \;\text{ уравнение окружности}\]
Мнимая часть дает
\[r = { 2\text{Im}(\Gamma) \over (1 - \text{Re}(\Gamma))^2 + \text{Im}^2(\Gamma) }\]
\[x^2 \left[ (1 - \text{Re}(\Gamma))^2 + \text{Im}^2(\Gamma) \right] - 2x\text{Im}(\Gamma) + \overbrace{1 - 1}^{=0} = 0 \; \left( \begin{matrix} \text{умножаем на x и} \\ \text{добавляем значение,} \\ \text{равное нулю} \end{matrix} \right)\]
\[\left[ (1 - \text{Re}(\Gamma))^2 + \text{Im}^2(\Gamma) \right] - {2\over x}\text{Im}(\Gamma) + {1 \over x^2} = {1 \over x^2}\]
\[ (1 - \text{Re}(\Gamma))^2 + \left[ \text{Im}^2(\Gamma) - {2\over x}\text{Im}(\Gamma) + {1 \over x^2} \right] = {1 \over x^2}\]
\[ (1 - \text{Re}(\Gamma))^2 + \left[ \text{Im}(\Gamma) - {1 \over x} \right]^2 = {1 \over x^2} \; \text{(уравнение окружности)}\]
Результат для действительной части показывает, что на комплексной плоскости с координатами (Re(Γ), Im(Γ)) все возможные импедансы с заданным нормированным сопротивлением r находятся на окружности с
\[Центр = \left\{ { r \over 1 +r}, 0 \right\}\]
\[Радиус = { 1 \over 1 +r }\]
Так как нормированное сопротивление r изменяется от 0 до ∞, мы получаем семейство окружностей, полностью лежащих в области коэффициента отражения |Γ| ≤ 1
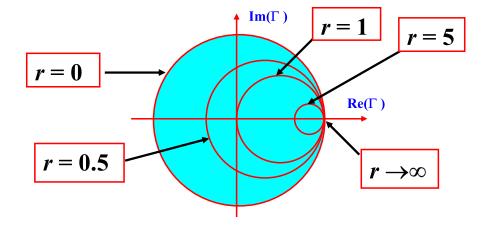
Результат для мнимой части показывает, что на комплексной плоскости с координатами (Re(Γ), Im(Γ)) все возможные импедансы с заданным нормированным реактивным сопротивлением x находятся на окружности с
\[Центр = \left\{ 1, { 1 \over x} \right\} \]
\[Радиус = { 1 \over x }\]
Так как нормированное реактивное сопротивление x изменяется от –∞ до +∞, мы получаем семейство дуг, лежащих в области коэффициента отражения |Γ| ≤ 1
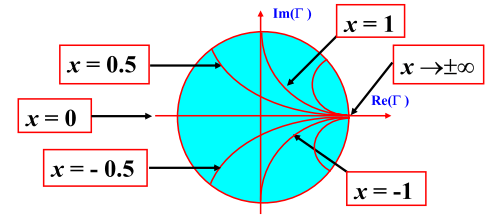
Базовые задачи применения диаграммы Смита для линии без потерь
- Задан Z(d) → найти Γ(d)
Задан Γ(d) → найти Z(d) - Задан ΓR и ZR → найти Γ(d) и Z(d)
Задан Γ(d) и Z(d) → найти ΓR и ZR - Найти dmax и dmin (максимальное и минимальное местоположения для заданного коэффициента стоячей волны)
- Найти коэффициент стоячей волны по напряжению (КСВ, КСВН, VSWR)
- Задан Z(d) → найти Y(d)
Задан Y(d) → найти Z(d)
Задан Z(d) → найти Γ(d)
- Нормализовать импеданс
\[z_n(d) = {Z(d) \over Z_0} = {R \over Z_0} + j{ X \over Z_0 } = r +jx \] - Найти окружность постоянного нормированного сопротивления r
- Найти дугу постоянного нормированного реактивного сопротивления x
- Пересечение этих двух кривых указывает на коэффициент отражения в комплексной плоскости. На диаграмме непосредственно указаны амплитуда и фазовый угол Γ(d)
Пример: найти Γ(d), исходя из заданных условий
\[Z(d) = 25 +j100 \; Ом; \quad Z_0 = 50 \; Ом\]
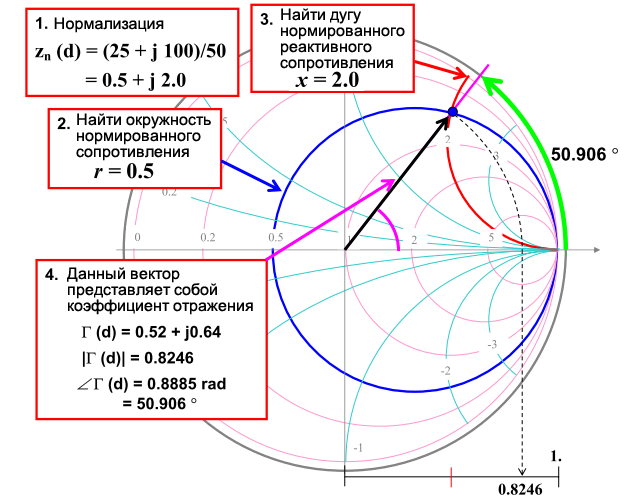
Задан Γ(d) → найти Z(d)
- Определить точку на комплексной плоскости, представляющую на диаграмме заданный коэффициент отражения Γ(d).
- Прочитать значения нормированного активного сопротивления r и нормированного реактивного сопротивления x, которые соответствуют точке коэффициента отражения.
- Нормированный импеданс равен
\[z_n(d) = r +jx \]
а реальный импеданс равен
\[Z(d) = Z_0 z_n(d) = Z_0(r+jx) = Z_0 r + j Z_0 x \]
Задан ΓR и ZR ↔ найти Γ(d) и Z(d)
ПРИМЕЧАНИЕ: величина коэффициента отражения постоянна вдоль линии передачи без потерь, заканчивающейся нагрузкой, поскольку
\[| \Gamma(d)| = |\Gamma_R \exp(-j2\beta d)| = |\Gamma_R|\]
Поэтому на комплексной плоскости окружность с центром в начале координат и радиусом |ΓR| представляет все возможные коэффициенты отражения, найденные вдоль линии передачи. Когда окружность постоянной величины коэффициента отражения рисуется на диаграмме Смита, можно определить значение импеданса линии в любом месте.
Графическая пошаговая процедура:
- Определить на диаграмме Смита коэффициент отражения нагрузки ΓR и нормализованный импеданс нагрузки ZR.
- Нарисовать окружность постоянной амплитуды коэффициента отражения |Γ(d)|=|ΓR|.
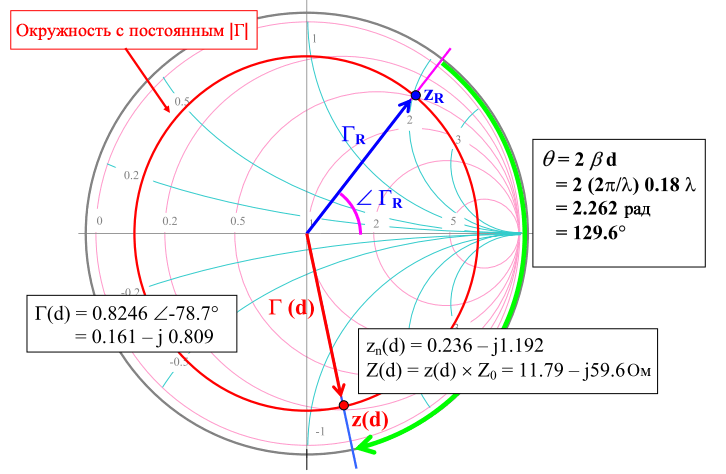
- Начиная с точки, представляющей нагрузку, перемещайтесь по окружность по часовой стрелке на угол
\[\theta = 2 \beta d = 2 { 2\pi \over \lambda } d\] - Новое местоположение на диаграмме соответствует местоположению d на линии передачи. Здесь значения Γ(d) и Z(d) могут быть считаны с диаграммы, как и раньше.
Пример:
Дано
\[Z(d) = 25 +j100 \; Ом; \quad Z_0 = 50 \; Ом\]
найти Z(d) и Γ(d) для d = 0,18λ
Даны ΓR и ZR → найти dmax и dmin
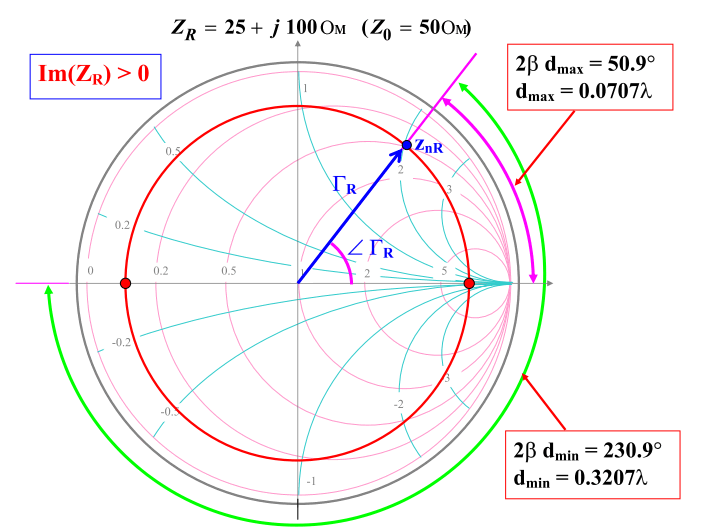
- Определить на диаграмме Смита коэффициент отражения нагрузки ΓR или нормированный импеданс нагрузки ZR.
- Начертить окружность постоянной амплитуды коэффициента отражения |Γ(d)|=|ΓR|. Окружность пересекает действительную ось коэффициента отражения в двух точках, которые указывают на dmax (когда Γ(d) = действительное положительное) и на dmin (когда Γ(d) = действительное отрицательное).
- Реально используемая диаграмма Смита предоставляет внешнюю градуировку, где непосредственно могут быть определены расстояния, нормированные на длину волны. Углы между вектором ΓR и вещественной осью, также обеспечивают способ для вычисления dmax и dmin
Пример: найти dmax и dmin для
\[Z(d) = 25 +j100 \; Ом; \quad Z(d) = 25 - j100 \; Ом \quad (Z_0 = 50 \; Ом) \]

Заданы ΓR и ZR → найти коэффициент стоячей волны по напряжению (КСВН, VSWR)
Коэффициент стоячей волны по напряжению (КСВН, VSWR) определяется как
\[КСВН = { V_{max} \over V_{min} } = { 1 + |\Gamma_R| \over 1 - |\Gamma_R| }\]
Нормированный импеданс на максимальном расстоянии шаблона коэффициента стоячей волны определяется выражением
\[z_n(d_{max}) = { 1 + \Gamma(d_{max}) \over 1 - \Gamma(d_{max})} = { 1 + |\Gamma_R| \over 1 - |\Gamma_R| } = КСВН!!!\]
Эта величина всегда вещественна и ≥ 1. КСВН получить на диаграмме Смита просто, прочитав значение (действительного) нормированного импеданса в точке dmax, где Γ является действительным и положительным.
Графическая пошаговая процедура:
- Определить на диаграмме Смита коэффициент отражения нагрузки ΓR и нормированный импеданс нагрузки ZR.
- Начертить окружность постоянной амплитуды коэффициента отражения |Γ(d)|=|ΓR|.
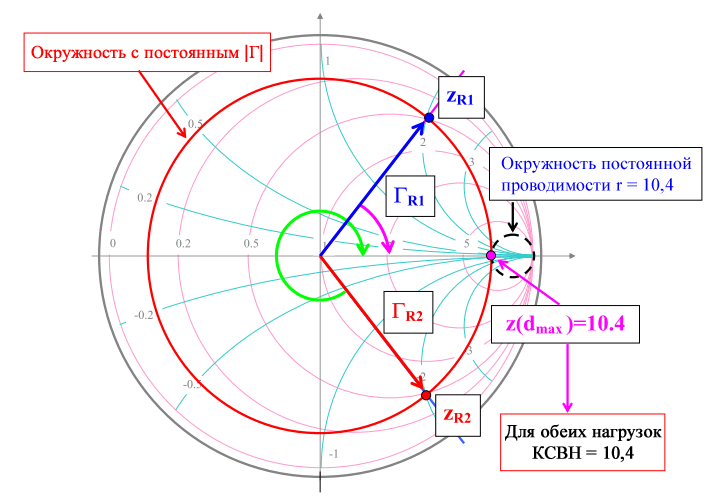
- Найти пересечение этой окружности с действительной положительной осью коэффициента отражения (соответствует точке dmax на линии передачи).
- Окружность постоянного нормированного активного сопротивления будет также пересекать эту точку. Прочитайте или интерполируйте значение нормированного активного сопротивления, чтобы определить КСВН.
Пример: найти КСВН для
\[Z(d) = 25 +j100 \; Ом; \quad Z(d) = 25 - j100 \; Ом \quad (Z_0 = 50 \; Ом) \]
Задан Z(d) ↔ найти Y(d)
Примечание: нормированные импеданс и адмитанс определяются как
\[z_n(d) = { 1 + \Gamma(d) \over 1 - \Gamma(d)} \]
\[y_n(d) = { 1 - \Gamma(d) \over 1 + \Gamma(d)} \]
Поскольку
\[\Gamma \left( d + {\lambda \over 4} \right) = - \Gamma(d)\]
то
\[z_n \left( d + {\lambda \over 4} \right) = { 1 + \Gamma \left( d + {\lambda \over 4} \right) \over 1 - \Gamma \left( d + {\lambda \over 4} \right) } = { 1 - \Gamma(d) \over 1 + \Gamma(d) } = y_n (d)\]
Помните, что равенство
\[z_n \left( d + {\lambda \over 4} \right) = y_n (d)\]
справедливо только для нормированных импеданса и адмитанса. Реальные значения могут быть получены по формулам:
\[Z \left( d + {\lambda \over 4} \right) = Z_0 \cdot z_n \left( d + {\lambda \over 4} \right) \]
\[Y(d) = Y_0 \cdot y_n(d) = { y_n(d) \over Z_0 }\]
где Y0=1/Z0 – характеристическая проводимость линии передачи.
Графическая пошаговая процедура:
- Определить на диаграмме Смита коэффициент отражения нагрузки ΓR и нормированный импеданс нагрузки ZR.
- Начертить окружность постоянной амплитуды коэффициента отражения |Γ(d)|=|ΓR|.
- Нормированный адмитанс находится в точке на окружности постоянного |Γ|, которая диаметрально противоположна нормированному импедансу.
Пример: найти YR при
\[Z(d) = 25 +j100 \; Ом; \quad (Z_0 = 50 \; Ом) \]
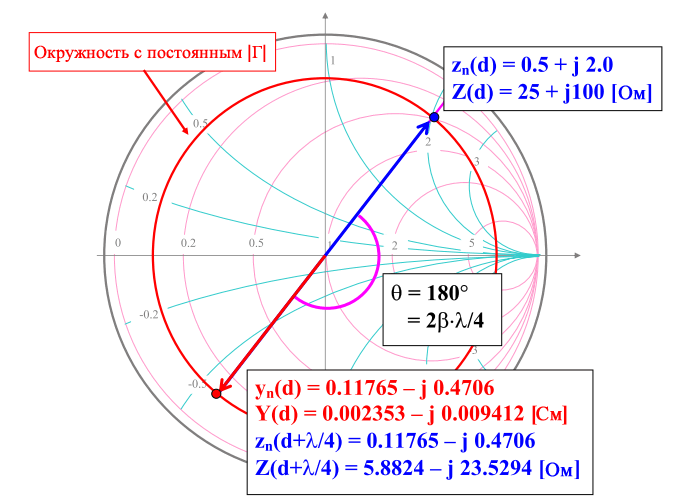
Диаграмма Смита может использоваться для полных проводимостей линии, просто сдвинув точку на место адмитанса. После этого можно перемещаться по диаграмме, читая числовые значения просто как представляющие адмитансы.
Давайте рассмотрим терминологию импеданса-адмитанса:
| Импеданс | = | Активное сопротивление | + | j Реактивное сопротивление |
| Z | = | R | + | jX |
| Адмитанс | = | Активная проводимость | + | j Реактивная проводимость |
| Y | = | G | + | jB |
На диаграмме импеданса правильный коэффициент отражения всегда представлен вектором, соответствующим нормированному импедансу. Диаграммы, специально подготовленные для адмитансов, модифицируются, чтобы обеспечить правильный коэффициент отражения в соответствии с адмитансом.
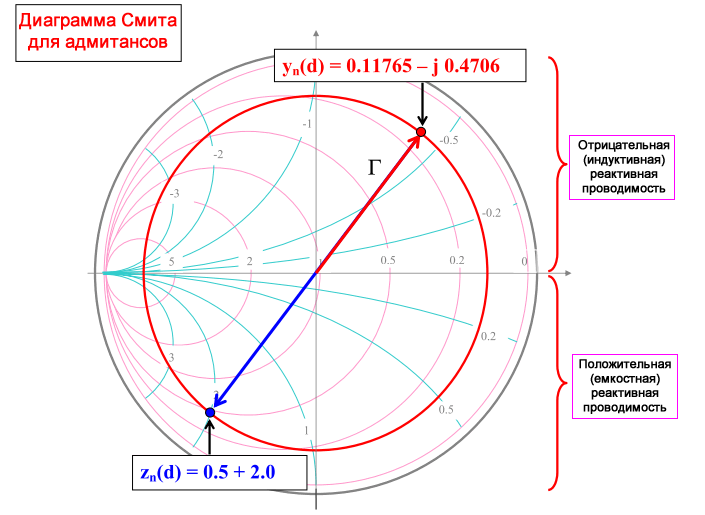
Поскольку связанные импеданс и адмитанс находятся на противоположных сторонах одной и той же диаграммы Смита, мнимые части всегда имеют разные знаки.
Поэтому положительное (индуктивное) реактивное сопротивление соответствует отрицательной (индуктивной) реактивной проводимости, а отрицательное (емкостное) реактивное сопротивление соответствует положительной (емкостной) реактивной проводимости.
Аналитически нормированные импеданс и адмитанс связаны следующим образом:
\[z_n = r + jx\]
\[y_n = g + jb = { 1 \over r + jx}\]
\[y_n = { r - jx \over (r+jx)(r-jx)} = {r - jx \over r^2 + x^2}\]
Следовательно:
\[g= { r \over r^2 + x^2}\]
\[b = - {x \over r^2 + x^2}\]
