Измерение температуры с помощью термистора NTC

Узнайте о термисторах и о том, как запрограммировать Arduino для измерения их данных.

Вы когда-нибудь задумывались над тем, как некоторые устройства, такие как термостаты, нагревательные площадки 3D принтеров, автомобильные двигатели и печи измеряют температуру? В этой статье вы можете это узнать!

Знать температуру может быть очень полезно. Знание температуры может помочь регулировать температуру в помещении до комфортного значения, гарантировать, что нагревательная площадка 3D принтера была достаточно горячей, чтобы такие материалы, как ABS, прилипали к ее поверхности, а также предотвратить перегрев двигателя или не допустить сжигания приготавливаемой еды.

В данной статье мы рассматриваем только один тип датчика, способного измерять температуру. Этот датчик называется термистором.

Термистор обладает сопротивлением, которое намного сильнее зависит от температуры, чем сопротивление других типов резисторов.

Мы буде использовать Arduino для измерения и обработки показаний термистора, после чего мы преобразуем эти показания в удобный для чтения формат единиц измерения температуры.

Ниже приведена фотография термистора, который мы собираемся использовать:

Необходимые компоненты

Комплектующие

• Arduino (Mega или Uno или любая другая модель);
• несколько перемычек;
• паяльник и припой (возможно, понадобится, если ваш термистор не будет влезать в разъемы на плате Arduino).

Программное обеспечение

• Arduino IDE

Теория

При типовом использовании резистора вы не хотите, чтобы его сопротивление менялось при изменении температуры. Это не реально в реальной жизни, можно лишь обеспечить небольшое изменение сопротивления при большом изменении температуры. Если бы это было не так, то резисторы странно влияли бы на работу схем, например, светодиод мог бы светиться намного ярче или тусклее по мере изменения температуры окружающей среды.

Но что, если вы действительно хотите, чтобы яркость светодиода была функцией температуры? Здесь появляется термистор. Как вы могли догадаться, у термистора сопротивление сильно изменяется при небольшом изменении температуры. Чтобы проиллюстрировать это, ниже приведена кривая изменения сопротивления термистора:

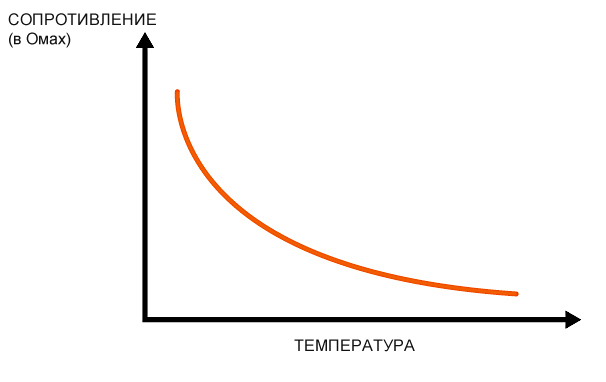
На рисунке показаны лишь единицы измерения без фактических значений, так как диапазон сопротивлений зависит от типа конкретного термистора. Как вы можете заметить, по мере увеличения температуры сопротивление терморезистора уменьшается. Это является отличительным свойством резистора с отрицательным температурным коэффициентом (Negative Temperature Coefficient), или, кратко, NTC термистора.

Существуют также терморезисторы с положительным температурным коэффициентом (Positive Temperature Coefficient, PTC), сопротивление которых увеличивается по мере роста температуры. Однако, PTC термисторы имеют своего рода точку перелома и сильно меняют сопротивление при некоторой температуре. Это делает взаимодействие с PTC термисторами чуть более сложным. По этой причине в большинстве дешевых измерителей температуры предпочтительнее использовать NTC термисторы.

В оставшейся части статьи, как вы можете догадаться, мы будем говорить о терморезисторах типа NTC.

Четыре подхода к нахождению формулы для построения кривой

Теперь, когда мы лучше понимаем поведение термисторов, вы можете удивиться, как мы можем использовать Arduino для измерения температуры. Кривая на графике выше нелинейна и, следовательно, простое линейное уравнение нам не подходит (на самом деле мы можем вывести уравнение, но об этом позже).

Так что же делать?

Прежде чем продолжить, подумайте, как бы вы это сделали на Arduino или даже в схеме без микропроцессорных компонентов.

Существует несколько способов решения этой проблемы, которые перечислены ниже. Это далеко не полный список всех методик, но он покажет вам некоторые популярные подходы.

Метод 1

Некоторые производители предоставляют настолько полную информацию, что в ней содержится весь график, отображающий определенные диапазоны целочисленных значений температуры и сопротивления (типовые значения). Один такой термистор может быть найден в техническом описании от компании Vishay.

Как, имея такие подробные данные, можно было бы реализовать измерение температуры на Arduino. Вам нужно было бы жестко прописать в коде все эти значения в огромной таблице поиска или очень длинных структурах управления "switch...case" или "if...else".

А если производитель не удосужился предоставить подробную таблицу, то вам придется самостоятельно измерить каждую точку для формирования такой таблицы. Этот день будет для программиста довольно уныл. Но этот метод не так уж и плох и имеет место в использовании. Если текущий проект проверяет лишь несколько точе или даже небольшой диапазон, этот способ может быть предпочтительным. Например, одна такая ситуация возникает, если вы хотите измерить, находятся ли значения выбранных диапазонах температур, и зажечь светодиод для индикации этого состояния.

Но в нашем проекте мы хотим измерять температуру в почти непрерывном диапазоне и отправлять показания на монитор последовательного порта, поэтому этот метод использовать не будем.

Метод 2

Вы можете попытаться «линеаризовать» реакцию термистора, добавив к нему дополнительную схему.

Одним из популярных способов выполнения этого является подключение резистора параллельно термистору. Некоторые микросхемы предлагают сделать это за вас.

Определение того, как выбрать и линеаризовать участок кривой, вместе с выбором правильного номинала резистора – это тема для отдельной статьи. Этот подход хорош, если микропроцессор не может вычислять выражения с плавающей запятой (например, PICAXE), поскольку он упрощает реакцию в некотором диапазоне температур до линейного характера. Это также упрощает проектирование схемы, в которой нет микропроцессора.

Но у нас в этой статье микропроцессор используется, и мы хотим измерять температуру во всем диапазоне.

Метод 3

Вы можете взять данные из таблицы в техническом описании или (если нравятся извращения) сформировать собственную таблицу, выполнив самостоятельные измерения и воссоздав график в чем-то типа Excel. Затем вы можете использовать функцию подгонки кривой для создания формулы этой кривой. Это неплохая идея, и вся выполненная работа даст красивую формулу, которую вы сможете использовать в программе. Но это займет некоторое время для предварительной обработки данных.

Хотя это разумный подход, мы не хотим зависеть от анализа всех этих данных. Кроме того, каждый термистор немного отличается (но, конечно, это не проблема, если допуск довольно низок).

Метод 4

Оказывается, есть общая формула для подгонки кривой, предназначенная для устройств типа термисторов. Она называется уравнением Штейнхарта-Харта. Ниже представлена его версия (в других версиях используются члены во второй и степени):

\[\frac{1}{T}=A+B\ln(R)+C(\ln(R))^3\]

где R – сопротивление терморезистора при температуре T (в Кельвинах).

Это общее уравнение кривой, подходящее для всех типов NTC термисторов. Аппроксимация связи температуры и сопротивления «достаточно подходит» для большинства применений.

Обратите внимание, что уравнение нуждается в константах A, B и C. Для разных термисторов они различаются и должны быть либо заданы, либо вычислены. Поскольку мы имеем три неизвестных, вам необходимо выполнить три измерения сопротивления при определенных температурах, которые затем могут быть использованы для создания трех уравнений и определения значений этих констант.

Даже для тех из нас, кто хорошо знают алгебру, это всё еще слишком трудоемко.

Вместо этого, есть еще более простое уравнение, которое менее точно, но содержит только одну константу. Эта константа обозначена как β, и поэтому уравнение называется β-уравнением.

\[\frac{1}{T}=\frac{1}{T_o}+(\frac{1}{\beta})\cdot\ln\left(\frac{R}{R_o}\right)\]

где R₀ – сопротивление при контрольной температуре T₀ (например, сопротивление при комнатной температуре). R – сопротивление при температуре T. Температуры указываются в Кельвинах. β обычно указывается в техническом описании; а если нет, то вам необходимо только одно измерение (одно уравнение) для расчета этой константы. Это уравнение я буду использовать для взаимодействия с нашим термистором, поскольку оно является самым простым из тех, с которыми я столкнулся, и не нуждается в линеаризации реакции термистора.

Измерение сопротивления с помощью Arduino

Теперь, когда мы выбрали метод построения кривой, мы должны выяснить, как реально измерить сопротивление с помощью Arduino, прежде чем мы сможем передать информацию о сопротивлении в β-уравнение. Мы можем сделать это используя делитель напряжения:

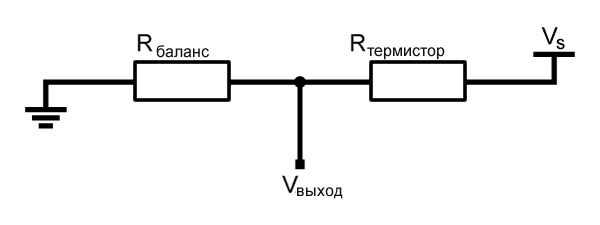
Это будет наша схема взаимодействия с термистором. Когда термистор определит изменение температуры, это отразится на выходном напряжении.

Теперь, как обычно, мы используем формулу для делителя напряжения.

\[V_{выход}=V_{s}\cdot(\frac{R_{баланс}}{R_{термистор}+R_{баланс}})\]

Но нам неинтересно выходное напряжение V_выход, нас интересует сопротивление термистора R_{термистор}. Поэтому мы выразим его:

\[R_{термистор}=R_{баланс}\cdot(\frac{V_s}{V_{выход}}-1)\]

Это намного лучше, но нам необходимо измерить наше выходное напряжение, а также напряжение питания. Так как мы используем встроенный АЦП Arduino, то можем представить напряжение, как числовое значение на определенной шкале. Итак, конечный вид нашего уравнения показан ниже:

\[R_{термистор}=R_{баланс}\cdot(\frac{D_{max}}{D_{измеренное}}-1)\]

Это работает потому, что не имеет значения, как мы представляем напряжение (в вольтах или в цифровых единицах), эти единицы сокращаются в числителе и знаменателе дроби, оставляя безразмерное значение. Затем мы умножаем его на сопротивление, чтобы получить результат в омах.

D_max у нас будет равно 1023, так как это самое большое число, которое может выдать наш 10-разрядный АЦП. D_{измеренное} – это измеренное значение аналого-цифровым преобразователем, которое может быть в диапазоне от нуля до 1023.

Всё! Теперь можно приступить к сборке!

Соберем это

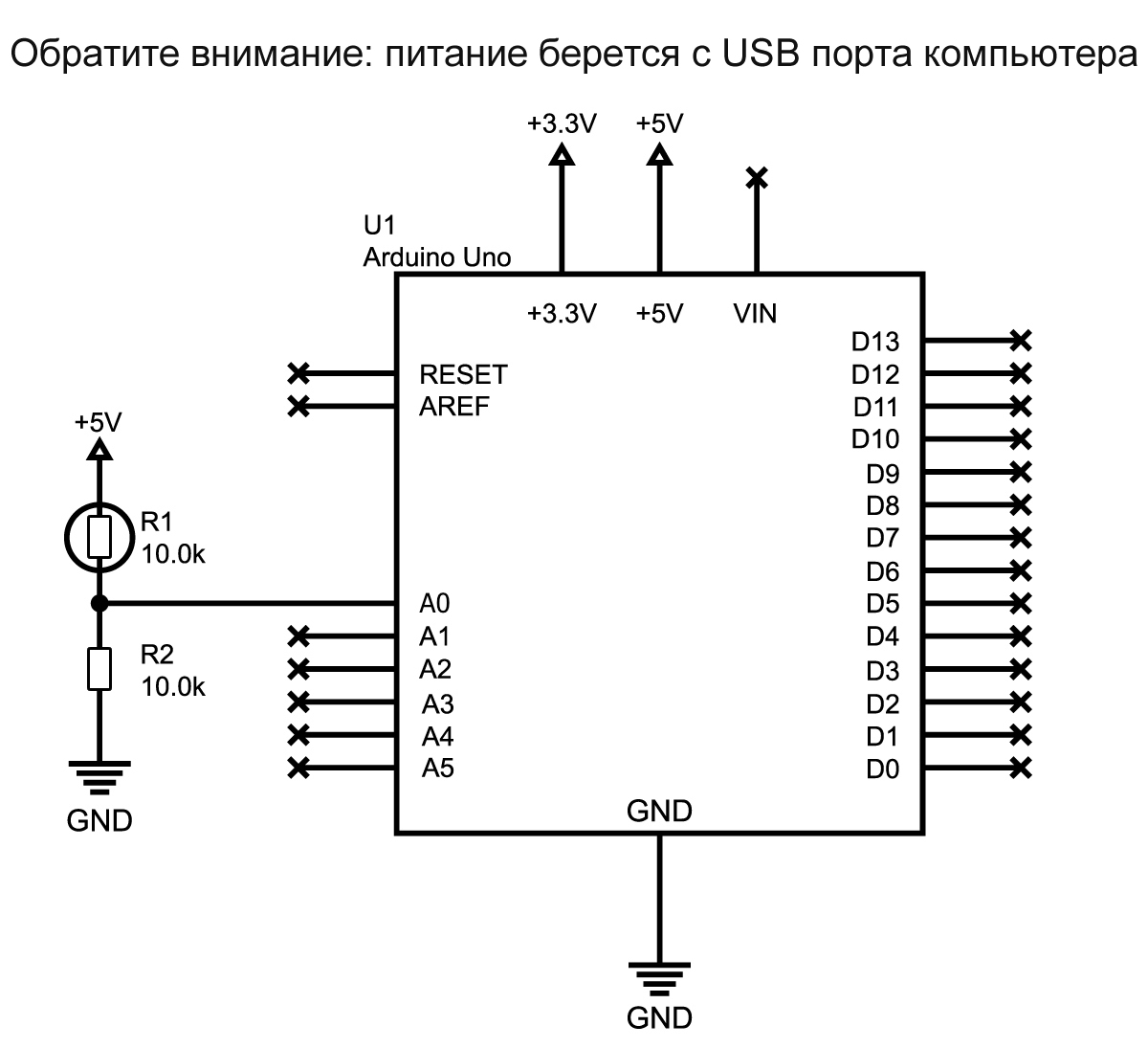
Я использовал термистор TH10K.

Также я использовал резистор 10 кОм в качестве R_баланс в нашем делителе напряжения. Константы β у меня не было, поэтому я рассчитал ее сам.

Ниже приведена полная схема устройства. Она довольно проста.

А так выглядит конечный макет:

Код программы для Arduino

Код снабжен большим количеством комментариев, чтобы помочь вам понять логику программы.

В основном он измеряет напряжение на делителе, вычисляет температуру, а затем показывает ее в терминале последовательного порта.

Для забавы добавлены также некоторые операторы "if...else", чтобы показать, как вы можете действовать в зависимости от диапазона температур.

//===============================================================================
//  Константы
//===============================================================================
// Связанные с термистором:

/* Здесь у нас несколько констант, которые упрощают редактирование кода.
   Пройдемся по ним.

   Чтение из АЦП может дать одно значение при одной выборке, а затем немного
   отличающееся значение при следующей выборке. Чтобы избежать влияния шумов,
   мы можем считывать значения с вывода АЦП несколько раз, а затем усреднять
   значения, чтобы получить более постоянное значение. Эта константа используется
   в функции readThermistor. */
const int    SAMPLE_NUMBER      = 10;

/* Чтобы использовать бета уравнение, мы должны знать номинал второго резистора
   в нашем делителе. Если вы используете резистор с большим допуском, например,
   5% или даже 1%, измерьте его и поместите результат в омах сюда. */
const double BALANCE_RESISTOR   = 9710.0;

// Это помогает вычислять сопротивление термистора (подробности смотрите в статье).
const double MAX_ADC            = 1023.0;

/* Эта константа зависит от термистора и должна быть в техническом описании, или
   смотрите статью, как рассчитать ее, используя бета-уравнение. */
const double BETA               = 3974.0;

/* Необходима для уравнения преобразования в качестве "типовой" комнатной
   температуры. */
const double ROOM_TEMP          = 298.15;   // комнатная температура в Кельвинах

/* Термисторы обладают типовым сопротивлением при комнатной температуре,
   укажем его здесь. Опять же, необходимо для уравнения преобразования. */
const double RESISTOR_ROOM_TEMP = 10000.0;

//===============================================================================
//  Переменные
//===============================================================================
// Здесь мы будем хранить текущую температуру
double currentTemperature = 0;

//===============================================================================
//  Объявления выводов
//===============================================================================
// Входы:
int thermistorPin = 0;  // Вход АЦП, выход делителя напряжения


//===============================================================================
//  Инициализация
//===============================================================================
void setup() 
{ 
  // Установить скорость порта для отправки сообщений
  Serial.begin(9600);
}

//===============================================================================
//  Основной цикл
//===============================================================================
void loop() 
{
  /* Основной цикл довольно прост, он печатает температуру в монитор последовательного
     порта. Сердце программы находится в функции readThermistor. */
  currentTemperature = readThermistor();
  delay(3000);
  
  /* Здесь описываем, что делать, если температура слишком высока, слишком низка
     или идеально подходит. */
  if (currentTemperature > 21.0 && currentTemperature < 24.0)
  {
    Serial.print("It is ");
    Serial.print(currentTemperature);
    Serial.println("C. Ahhh, very nice temperature.");
  } 
  else if (currentTemperature >= 24.0)
  {
    Serial.print("It is ");
    Serial.print(currentTemperature);
    Serial.println("C. I feel like a hot tamale!");
  } 
  else
  {
    Serial.print("It is ");
    Serial.print(currentTemperature);
    Serial.println("C. Brrrrrr, it's COLD!");
  }
}

//===============================================================================
//  Функции
//===============================================================================
/////////////////////////////
////// readThermistor ///////
/////////////////////////////
/*
Эта функция считывает значения с аналогового вывода, как показано ниже.
Преобразует входное напряжение в цифровое представление с помощью аналого-цифрового
преобразования. Однако, это выполняется несколько раз, чтобы мы могли
усреднить значение, чтобы избежать ошибок измерения.
Это усредненное значение затем используется для расчета сопротивления термистора.
После этого сопротивление используется для расчета температуры термистора.
Наконец, температура преобразуется в градусы Цельсия. 
*/

double readThermistor() 
{
  // переменные
  double rThermistor = 0;            // Хранит значение сопротивления термистора
  double tKelvin     = 0;            // Хранит рассчитанную температуру
  double tCelsius    = 0;            // Хранит температуру в градусах Цельсия
  double adcAverage  = 0;            // Хранит среднее значение напряжения
  int    adcSamples[SAMPLE_NUMBER];  // Массив для хранения отдельных результатов
                                     // измерений напряжения

  /* Рассчитать среднее сопротивление термистора:
     Как упоминалось выше, мы будем считывать значения АЦП несколько раз,
     чтобы получить массив выборок. Небольшая задержка используется для
     корректной работы функции analogRead. */
  
  for (int i = 0; i < SAMPLE_NUMBER; i++) 
  {
    adcSamples[i] = analogRead(thermistorPin);  // прочитать значение на выводе и сохранить
    delay(10);        // ждем 10 миллисекунд
  }

  /* Затем мы просто усредняем все эти выборки для "сглаживания" измерений. */
  for (int i = 0; i < SAMPLE_NUMBER; i++) 
  {
    adcAverage += adcSamples[i];      // складываем все выборки . . .
  }
  adcAverage /= SAMPLE_NUMBER;        // . . . усредняем их с помощью деления

  /* Здесь мы рассчитываем сопротивление термистора, используя уравнение,
     описываемое в статье. */
  rThermistor = BALANCE_RESISTOR * ( (MAX_ADC / adcAverage) - 1);

  /* Здесь используется бета-уравнение, но оно отличается от того, что 
     описывалось в статье. Не беспокойтесь! Оно было перестроено, чтобы
     получить более "красивую" формулу. Попробуйте сами упростить уравнение,
     чтобы поупражняться в алгебре. Или просто используйте показанное здесь
     или то, что приведено в статье. В любом случае всё будет работать! */
  tKelvin = (BETA * ROOM_TEMP) / 
            (BETA + (ROOM_TEMP * log(rThermistor / RESISTOR_ROOM_TEMP)));

  /* Я буду использовать градусы Цельсия для отображения температуры.
     Я сделал это, чтобы увидеть типовую комнатную температуру, которая
     составляет 25 градусов Цельсия. */
  tCelsius = tKelvin - 273.15;  // преобразовать кельвины в цельсии

  return tCelsius;    // вернуть температуру в градусах Цельсия
}

Возможные следующие шаги

Всё в данной статье показывает довольно простой способ измерения температуры с помощью дешевого термистора. Есть еще пара способов улучшить схему:

• добавить небольшой конденсатор параллельно выходу делителя. Это стабилизирует напряжение и может даже устранить необходимость усреднения большого количества выборок (как было сделано в коде) – или, по крайней мере, мы сможете усреднять меньшее количество выборок;
• использовать прецизионные резисторы (допуск меньше 1%), чтобы получить более предсказуемые измерения. Если вам критична точность измерений, имейте в виду, что самонагревание термистора может повлиять на измерения; в данной статье самонагрев не компенсируется.

Конечно, термисторы – это только один из датчиков, используемых для измерения температуры. Другой популярный выбор – это микросхемы датчиков (пример работы с одной из них описан здесь). В этом случае вам не придется иметь дело с линеаризацией и сложными уравнениями. Два других варианта – это термопара и инфракрасный тип датчика; последний может измерять температуру без физического контакта, но он уже не так дешев.

Надеюсь, статья оказалась полезной. Оставляйте комментарии!

Теги