Математическая конструкция и свойства диаграммы Вольперта-Смита

Добавлено 2 мая 2016 в 14:10

Диаграмма Вольперта-Смита – инструмент, чрезвычайно полезный для инженеров и разработчиков, занимающихся радиочастотными цепями. В данной статье рассматривается математика создания диаграммы и её объяснение с точки зрения физики.

Введение

Диаграмма Вольперта-Смита используется с 1930-х годов в качестве метода решения различных задач проектирования в диапазоне радиочастот – в частности, согласование комплексных сопротивлений с помощью последовательно и параллельно включенных элементов – и обеспечивает удобный способ для нахождения решения без использования калькулятора. Для того, чтобы понять конструкцию диаграммы, вы должны понимать алгебру на уровне средней школы и основы комплексных чисел, а также иметь общее представление о комплексном сопротивлении (импедансе) в электронных схемах. Тем не менее, даже если вы не в совсем поймете приведенный ниже вывод, вы всё равно можете использовать диаграмму в своих разработках. Взяв стандартную формулу коэффициента отражения и манипулируя ею так, чтобы получить уравнения окружностей различных радиусов, мы сможем построить базовую диаграмму Вольперта-Смита. Это всё, чем на самом деле и является диаграмма Вольперта-Смита: набор окружностей, центры которых находятся в разных местах на графике или за его пределами, и каждая из которых представляет собой либо постоянное активное сопротивление, либо постоянное реактивное сопротивление.

Получение диаграммы Вольперта-Смита

После того, как мы закончим вывод диаграммы, ниже будет приведено несколько упрощенных изображений, показывающих, как полученные формулы могут быть использованы для получения конечного результата. Давайте начнем с формулы коэффициента отражения в зависимости от сопротивлений источника и нагрузки:

\[\Gamma=\frac{Z_{ист}-Z_{нагр}}{Z_{ист}+Z_{нагр}}\]

Коэффициент отражения – это просто отношение амплитуды отраженной волны к амплитуде падающей волны. Это главная формула, которую мы будем использовать, но с небольшими преобразованиями. Во-первых, нам необходимо немного упростить ее путем нормализации относительно Z_нагр, разделив каждый член в правой части формулы на Z_нагр:

\[\Gamma = \frac{\frac{Z_{ист}}{Z_{нагр}}-\frac{Z_{нагр}}{Z_{нагр}}}{\frac{Z_{ист}}{Z_{нагр}}+\frac{Z_{нагр}}{Z_{нагр}}}\]

\[\Gamma = \frac{Z_{O}-1}{Z_{O}+1}\]

где

\[Z_{O} = \frac{Z_{ист}}{Z_{нагр}}\]

Напомним, что Z_O является комплексным значением импеданса и может быть представлено в виде R + jX. Так как коэффициент отражения (который сейчас находится в полярной форме) может быть также представлен и в прямоугольных координатах (для этого мы будем использовать A + jB), приведенная выше формула может быть преобразована в следующую:

\[A + jB = \frac{R + jX -1}{R + jX + 1}\]

Круто! На данный момент мы получили уравнение в том виде, который нам необходим, чтобы начать построение диаграммы Вольперта-Смита. Следующий шаг – решение для действительной и мнимой частей равенства – возможно, самая сложная часть всего вывода, и даже тогда вам надо просто понимать идею комплексных сопряжений, чтобы выполнить этот шаг. Давайте продолжим и разделим уравнение на действительную и мнимую составляющие, сначала умножив на комплексное сопряженное число (это поможет, если вы разделите существующие действительные и мнимые части, используя скобки, как показано ниже):

\[A + jB = \frac{(R-1)+jX}{(R+1)+jX} \cdot \frac{(R+1)-jX}{(R+1)-jX}\]

\[A+jB = \frac{R^2-1+X^2+2jX}{(R+1)^2+X^2}\]

Теперь мы можем отделить действительную и мнимую составляющие. После чего необходимо будет выполнить два последних упрощения, и мы получим формулы для построения диаграммы Вольперта-Смита. Ниже приведены разделенные действительная и мнимая составляющие (назовем их уравнения 1 и 2):

\[A=\frac{R^2-1+X^2}{(R+1)^2+X^2} \text{ (Уравнение 1)}\]

\[B=\frac{2X}{(R+1)^2+X^2} \text{ (Уравнение 2)}\]

И, наконец, вам необходимо выполнить несколько алгебраических операций, чтобы вывести зависимость X² от A. В итоге получится уравнение 3:

\[X^2=\frac{A(R+1)^2-R^2+1}{1-A} \text{ (Уравнение 3)}\]

Это можно подставить в уравнение 2, чтобы получить первое из двух конечных уравнений, которое позволит нам определить круги постоянного активного сопротивления (уравнение 4):

\[(A-\frac{R}{R+1})^2 + B^2 = (\frac{1}{R+1})^2 \text{ (Уравнение 4)}\]

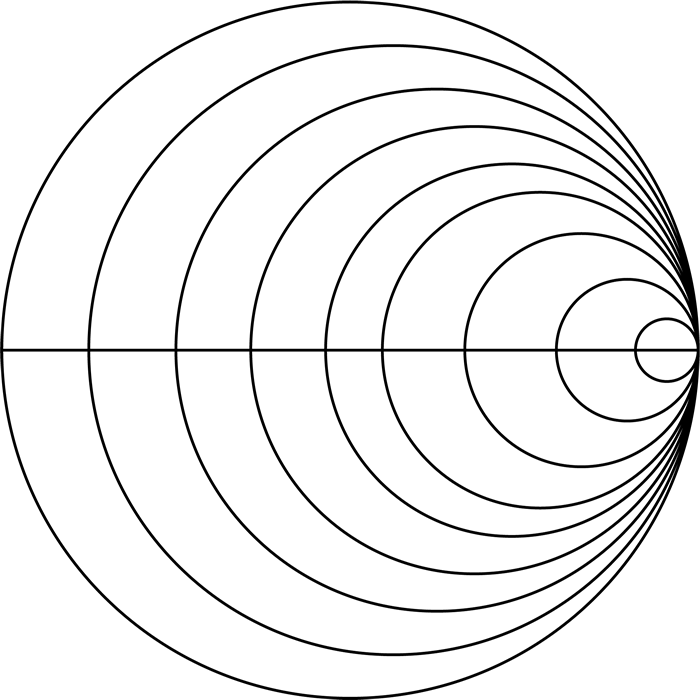
Выглядит знакомо? Это окружность радиусом \(\frac{1}{R+1}\) и центром в точке \((\frac{R}{R+1},\; 0)\). Изменяя значение R в уравнении, можно нарисовать каждую из окружностей на диаграмме Вольперта-Смита.

Аналогичным образом, выразив R (я использовал уравнение 2), вы получите решения выглядящие следующим образом:

\[R=\frac{\sqrt{-BX(BX-2)}-B}{B}\]

И, подставив это выражение в уравнение 1 и упростив полученное выражение, получим следующий результат:

\[(A-1)^2+(B-\frac{1}{X})^2=(\frac{1}{X})^2 \text{ (Уравнение 5)}\]

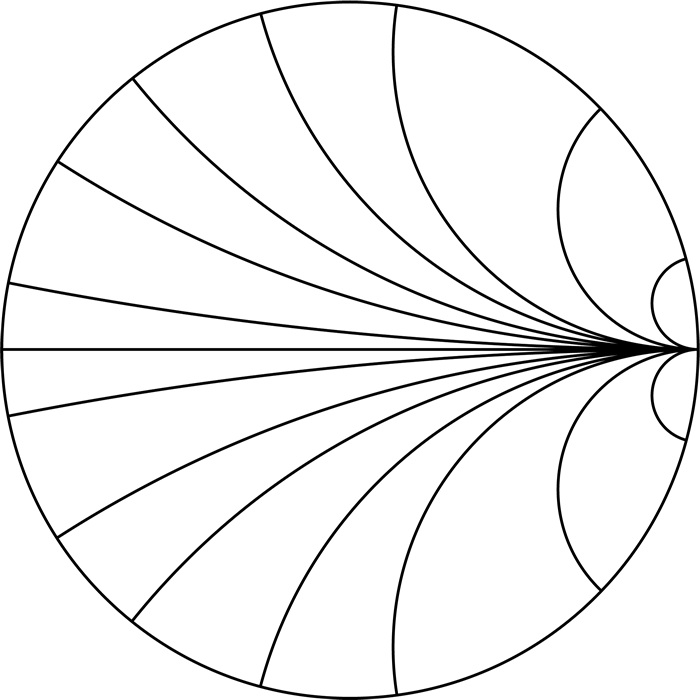
Как и предыдущий результат, это окружность радиусом \(\frac{1}{X}\), но на этот раз у нас два набора окружностей с центрами в \((1, 1/X)\). Это окружности (они появятся в виде дуг на диаграмме) постоянного реактивного сопротивления. Теперь вы можете увидеть, как строится диаграмма Вольперта-Смита, она состоит из окружностей постоянного активного сопротивления и дуг постоянного реактивного сопротивления. Ниже вы можете увидеть упрощенные изображения обоих уравнений, построенные по отдельности и вместе. Но сначала давайте поговорим о том, как интерпретировать диаграмму Вольперта-Смита с точки зрения физики.

Из полученных нами уравнений можно получить довольно много информации. Вот несколько моментов, на которые стоит обратить внимание:

при бесконечных R и X оба типа окружностей сходятся в одном месте (обычно изображается на крайне правой или на крайне левой стороне диаграммы). Это точка с координатами (1, 0);
установка R = 0 приведет к окружности с центром в точке (0, 0) на вашей диаграмме и с радиусом 1, который является «границей» диаграммы;
установка X = 0 приведет к бесконечному радиусу; это соответствует линии, пересекающей центр диаграммы. Как мы можем это интерпретировать? Эту линию часто называют действительной осью. Касательно реактивного сопротивления, линии выше действительной оси на диаграмме (положительные дуги из второго полученного уравнения) представляют собой индуктивные реактивные сопротивления, а линии ниже (отрицательные дуги) – емкостные реактивные сопротивления;
что произойдет, если R < 0? Стандартная диаграмма Вольперта-Смита не дает информации об этом, но ситуации с R, лежащим за границами диаграммы, предполагают возникновение колебаний в любой возможной цепи (что очень полезно знать);
на основе знаний, которые у нас теперь есть, об активном и реактивном сопротивлениях на диаграмме, мы знаем, что каждая точка представляет собой последовательную комбинацию активного и реактивного сопротивлений (R + jX). Это поможет нам при разработке.

Окружности постоянного активного сопротивления

Дуги постоянного реактивного сопротивления

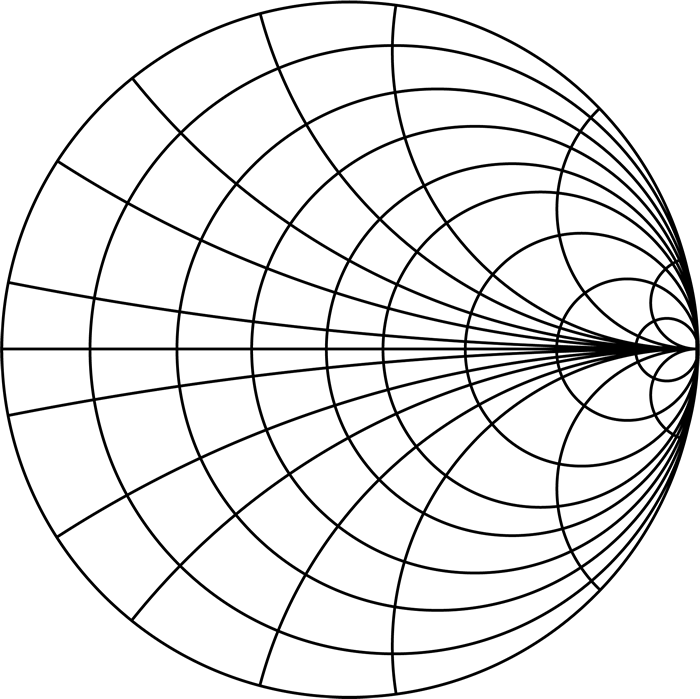
Окружности постоянного активного сопротивления и дуги постоянного реактивного сопротивления: базовая диаграмма Вольперта-Смита

Использование диаграммы Вольперта-Смита для работы с комплексными сопротивлениями

Так как же использовать диаграмму Вольперта-Смита? Для нанесения на диаграмму импеданса при расчете согласования комплексных сопротивлений лучше всего определить соответствующую окружность постоянного активного сопротивления (ту, которая соответствует действительной части вашего импеданса), а затем перемещаться по ее дуге, пока не найдете пересечение с соответствующим значением реактивного сопротивления.

Например, предположим, у вас есть комплексное сопротивление Z = 0,3 – 0,6j. Сначала найдите окружность постоянного активного сопротивления 0,3. Так как ваше сопротивление имеет отрицательное комплексное значение, то это представляет собой емкостное комплексное сопротивление в теоретической цепи, и вы должны двигаться против часовой стрелки по окружности активного сопротивления 0,3, чтобы найти, где она пересекается с дугой реактивного сопротивления –0,6 (если бы это значение было положительным, то оно представляло бы собой индуктивное реактивное сопротивление, и вы бы двигались по часовой стрелке). Вы можете продолжать выполнение построения для расчета согласования импедансов для ваших цепей, так как диаграмма Вольперта-Смита интуитивно понятна и в этом случае чрезвычайно полезна. Вам необходимо только выполнить следующие действия:

зная значение комплексного сопротивления нагрузки, найти его на диаграмме Вольперта-Смита и использовать его в качестве начальной точки;
если вы знаете выходное сопротивление источника, вы можете добавить последовательно компоненты (шунты будут упомянуты ниже) путем добавления и вычитания значений реактивных сопротивлений до тех пор, пока не получите необходимый импеданс.

Важно обратить внимание на два момента:

на практике вы часто можете обнаружить, что цифры на вашей диаграмме малы по сравнению со значениями составляющих комплексного сопротивления, которые вы хотите найти. Здесь снова вступает в игру нормализация; часто бывает удобнее всего нормализовать импеданс (например, Z = 200 + j400), в результате вы работаете с ним, деленным на некоторое значение, что делает построение диаграммы проще (часто это значение действительной части импеданса, но вы можете использовать и любое другое удобное для вас значение). Таким образом, вы сможете работать на менее заполненном участке диаграммы Вольперта-Смита, что приводит нас к следующему пункту;
при работе с диаграммой Вольперта-Смита легко оказаться в ситуации, когда вы будете вынуждены работать со значениями комплексных сопротивлений близко к точке (1, 0), и в этом случае у вас возникнут проблемы с ошибками в рассчитанных вами значениях. Вот поэтому лучше всего нормализовать значения вашего импеданса при работе с диаграммой, что позволит вам работать с более широкими дугами при согласовании импедансов и обеспечит постоянную точность по мере добавления компонентов в последовательность.

Последнее замечание – комплексная проводимость и диаграммы иммитанса (комплексных сопротивления и проводимости)

До сих пор мы не упоминали о комплексной проводимости на диаграмме Смита. Если вы не знаете, то комплексная проводимость (адмиттанс) является величиной, обратной комплексному сопротивлению (импедансу), или \(Y=\frac{1}{Z}\). Активное и реактивное сопротивления в этом случае соответствуют активной и реактивной проводимостям. На самом деле, построить аналогичную диаграмму для проводимостей удивительно просто – всё, что вам нужно сделать, это отразить диаграмму сопротивлений по горизонтали. Подобное преобразование очень важно, так как теперь у вас есть диаграмма, которая поможет вам при работе с шунтирующими компонентами (включенными между корпусом и линией связи, параллельно источнику и нагрузке), а не только с включенными последовательно.

Процесс нанесения проводимости на диаграмму противоположен – при добавлении индуктивности в цепь последовательно необходимо перемещать значение импеданса по часовой стрелке вдоль окружности постоянного активного сопротивления, а при добавлении шунтирующей индуктивности (включенной параллельно) необходимо перемещаться против часовой стрелки вдоль окружности постоянной активной проводимости; аналогично и с конденсаторами, шунтирующий конденсатор перемещает ваши значения по часовой стрелке на диаграмме комплексной проводимости, а конденсатор, включенный последовательно, – против часовой.

Сочетание обоих типов диаграмм даст вам то, что называется диаграммой комплексных сопротивления и проводимости (иммитанса), которая (как только вы добавите еще несколько деталей, не описанных в данной статье) становится еще более полезной, чем стандартная диаграмма Смита, хотя она и будет выглядеть более устрашающей для тех, кто не знает, как она была создана.

Надеюсь, эта статья дала вам ясное понимание того, как строится и как работает диаграмма Смита. В случае вопросов оставляйте комментарии ниже.